1. 서론

건물풍압은 건물의 고층화로 인한 높이의 증가로 건물설계 시 주요 설계 요소 중의 하나가 되었다. 또한 풍압은 외장재의 설계에 있어서 가장 중요한 설계 요소이다. 건물외벽에 작용하는 풍압은 구조적인 요소와 직결되고 구조적인 요소는 외벽 설계에 있어서 경제성과 직결되는 문제이기 때문이다. 특히, 고층 및 초고층 건물을 설계 시에는 그 중요성이 더욱 커진다.

외벽 설계에 있어서 정확한 풍압 분석은 구조적으로 안정하고 가장 경제적인 외벽을 구성하는데 결정적인 영향을 끼치게 되는 만큼 보다 정확한 풍압계산을 위해 실제적으로 풍동시험을 실시하는 것이 가장 바람직하지만 그렇지 못할 경우는 법규에 의한 해석(1)을 따르는 것이 일반적이다.

현재 고층 건물(20 m 이상 6층 이상)뿐만 아니라 초고층 건물(200 m 이상, 50층 이상)도 점점 늘어나고 있다. 또한 도심의 고층 건물 밀도가 증가하면서 좁은 건물 사이에 생겨나는 빌딩 풍에 대한 피해 사례는 매년 발생하고 있다.

우리나라에서는 아직 초고층 건물에 대한 건축법 중 풍압에 관한 내용은 풍 방향 및 풍 수직 방향에 관련한 풍동실험만을 실시하는 것을 규정(2)으로 하고 있다.

현재까지의 연구동향을 살펴보면, 풍 방향 및 풍 수직 방향에 관련한 풍동실험과 CFD에 관련한 연구가 주를 이룬다. Agerneh et al.(3)은 고층 건물이 받는 풍압을 풍동실험과 CFD를 함께 진행하여 비교하는 연구를 하였고 기존 건물의 앞, 뒤에 또 다른 건물을 설정하여 그에 따른 영향 또한 살펴보았다. Jeong et al.(4)은 실제 존재하는 건물에 대하여 풍동실험을 실시하고 그에 따른 풍압계수를 알아보기 위해 CFD 시뮬레이션을 도구로 수행하였다. Park et al.(5)은 중층 또는 저층 건축물에 작용하는 풍하중을 높이에 따라 알아보고 각 건축물의 풍상, 하면에 작용하는 평균 풍압분포의 특성을 규명하였다. Lee et al.(6)은 실존하는 고층 건축물의 풍속 연직분포를 알아보기 위해 풍동실험을 주로 실시하였다. Roh(7)는 국내에서 건물 외부 풍으로 인해 발생하는 빌딩 풍을 아파트 단지 내에 적용시켜 빌딩풍의 직접적인 영향을 CFD를 통해 해석하였다. 하지만 실제 아파트 건물 모델을 사용하였기 때문에 건물 설계 모델의 기준을 제시하지는 못하였다. Song(8)은 Texas Tech. Univ. (TTU)건물에 대해서 바람의 각도가 90°인 경우에 k-ω 난류 모델을 이용하여 건물 표면의 다양한 풍압계수를 예측하고 실험 데이터와 비교를 하였다. Jo et al.(9)에서도 풍동실험과 CFD 해석을 시행하였지만 특정한 지역과 건물을 해석한 연구이므로 범용적인 참고자료로 사용에 어려움이 있다. 이처럼 고층부터 저층 건물까지의 풍압분포에 관련된 연구는 활발히 진행 중이지만 빌딩 풍에 관련된 연구는 아직 기초적인 수준에 있으며, 그에 따른 설계 기준 또한 제대로 제시되지 않고 있다.

Fig. 1. CAARC(commonwealth advisory aeronautical council) building model.

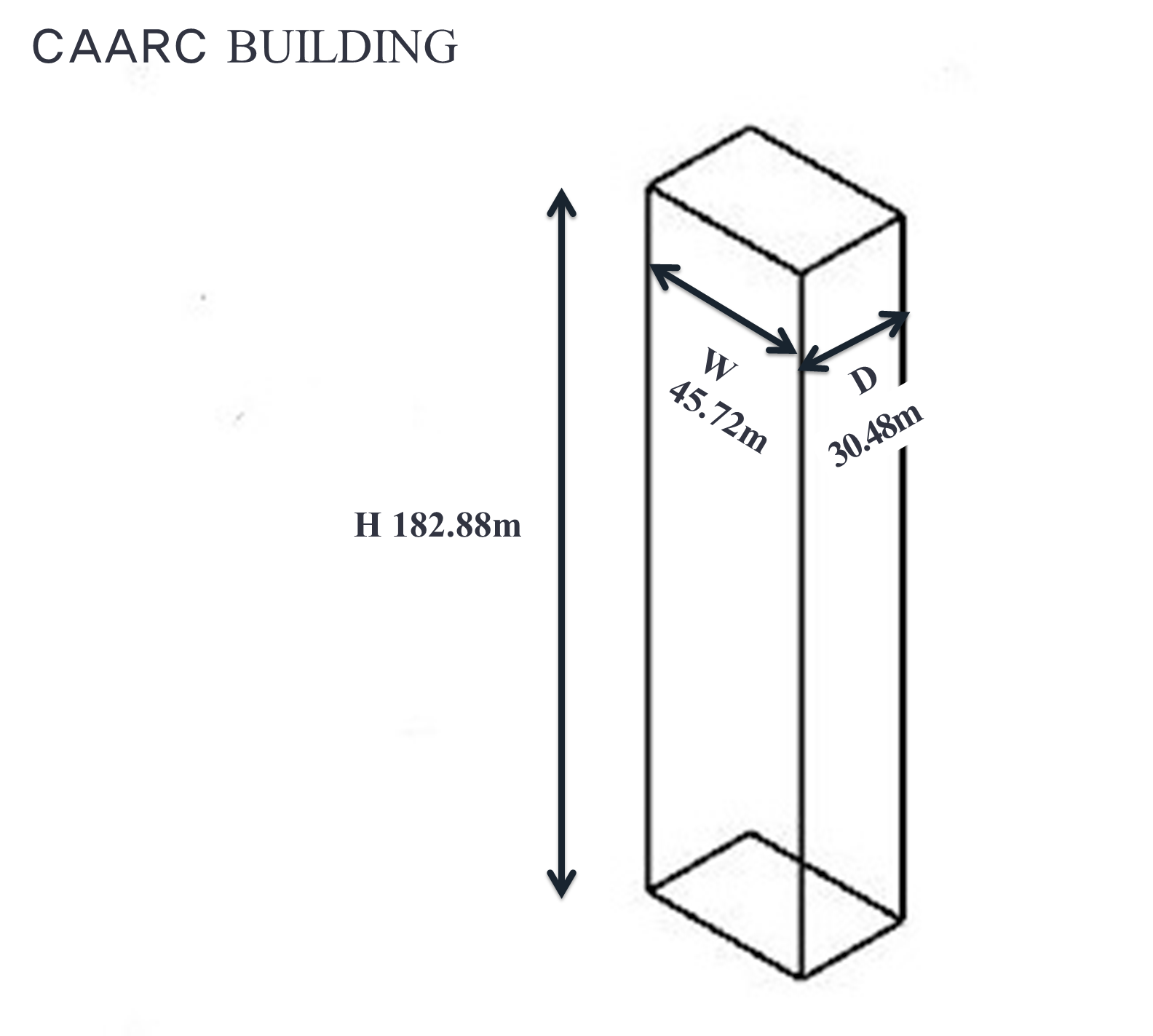
본 연구에서는 풍동실험과 CFD 해석을 같이 수행한 Agerneh et al.(3) 연구논문에 있는 CAARC 모델을 기준으로 선택하여 같은 조건으로 CFD 해석을 수행한다. CAARC 모델은 전형적인 박스형 건물로 주로 외국에서 연구된 사례가 많은 빌딩 모델 중 하나이다. Wardlaw와 Moss가 1970년에 제작한 모델로 풍동실험 연구 모델로도 쓰여 왔다. 본 연구는 풍향 및 빌딩 풍에 따른 빌딩의 풍압분포를 관찰하고 비교하기 위함이므로 기본적인 실험 결과 값이 존재하는 CAARC 모델을 선택했다. CAARC 모델의 크기는 가로 45.72 m(W), 폭 30.48 m(D), 높이 182.88 m(H)로 Fig. 1에 나타내었다. 이를 통해 CAARC 모델 건물이 받는 풍압분포를 확인하고 Agerneh et al.(3)의 연구논문과 데이터를 비교하여 신뢰도를 확보하고, 다음으로 풍향을 변화시켜 분석하여 최대풍압계수를 비교한다. 이어서 빌딩 풍을 생성하는 두 건물 사이의 거리와 두 건물과 CAARC 모델 사이의 거리를 조절했을 때의 빌딩 풍이 CAARC 모델에 영향을 미쳐 풍압분포가 어떻게 변하는지 확인한다. 이 후 결과를 바탕으로 고층 건물이나 아파트 단지 건물 설계 시 참고자료로 사용할 수 있도록 빌딩 풍의 영향을 받는 기준 범위를 제시하도록 한다.

2. 수치 해석

CFD에 의한 풍압 분포 해석을 하는 과정은 크게 4가지 절차로 수행하도록 한다.

(1) 대상 건물의 형상은 분석하는 목적에 맞게 설계한다.

(2) 전처리 과정으로 해석에 적합한 격자 계를 만든다.

(3) 만들어진 격자 계를 이용하여 물성치와 적절한 물리적 모델을 적용한다. 그리고 경계조건을 입력하고 수치해석을 수행한다.

(4) 마지막으로 계산 결과를 이용하여 해석에 적합한 풍압을 추출하는 후처리 과정으로 나누게 된다.

2.2 계산 영역 및 격자

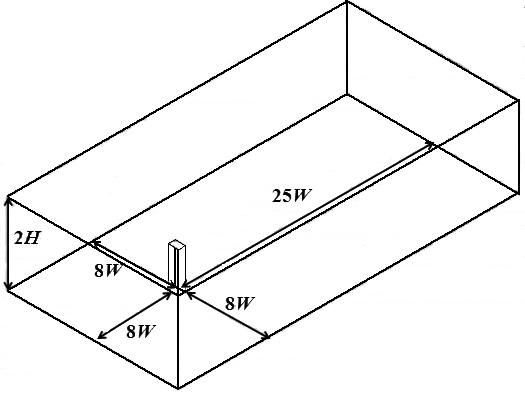
계산 영역은 Fig. 2와 같이 건물의 앞과 양 옆 방향으로는 8 W, 건물의 뒤 방향으로 25 W, 높이는 2 H가 되도록 구성하였다. 건물로 유입되는 바람의 방향은 건물과 수평하게 불어오는 것을 모사한 것이다. CAARC 모델의 실제 높이 182.88 m와 그 높이에서의 속도(12.7 m/s)를 기준으로 한 실제 건물의 레이놀즈수는 약 380,000으로 본 계산에서도 이 값을 사용하였다.

본 연구에서는 건물 벽 근처에서는 조밀격자를 생성하였으며 건물 벽으로부터 멀어질수록 성긴 격자를 생성하였다.

Fig. 2. Computational domain.

격자 생성은 ANSYS사의 FLUENT 전용 격자 생성 프로그램을 사용하였고 격자의 모양은 사면체로 결정하였다. 해석 모델은 건물의 축소 모델을 사용하였고 해석영역은 축소 건물 모델을 포함하는 3.10896 m⨯6.15696 m⨯1.46304 m으로 정하였다. 격자 개수에 대해서는 초기에 각각 100만 개, 50만 개로 하여 해석을 해본 결과, 전체적인 유동이 유사하였다. 본 연구에서는 유체의 세밀한 유동을 해석하기 보다는 전체적인 유동을 해석하여 어떠한 영향을 미치는지를 보는 것이 주목적이기 때문에 경제적인 문제를 고려하여 격자 개수를 50만 개로 설정하였다.

3. 계산 결과

풍압계수를 구하기 위해서 다음과 같은 풍압에 관한 공식을 고려하였다.

위의 식에서 비중량, λ는 1.23 kgf/m³, 풍속, U는 12.7 m/s으로 계산하여 풍압, P에 동압, λU²/2를 나눠서 풍압계수, C_p를 계산하였다.

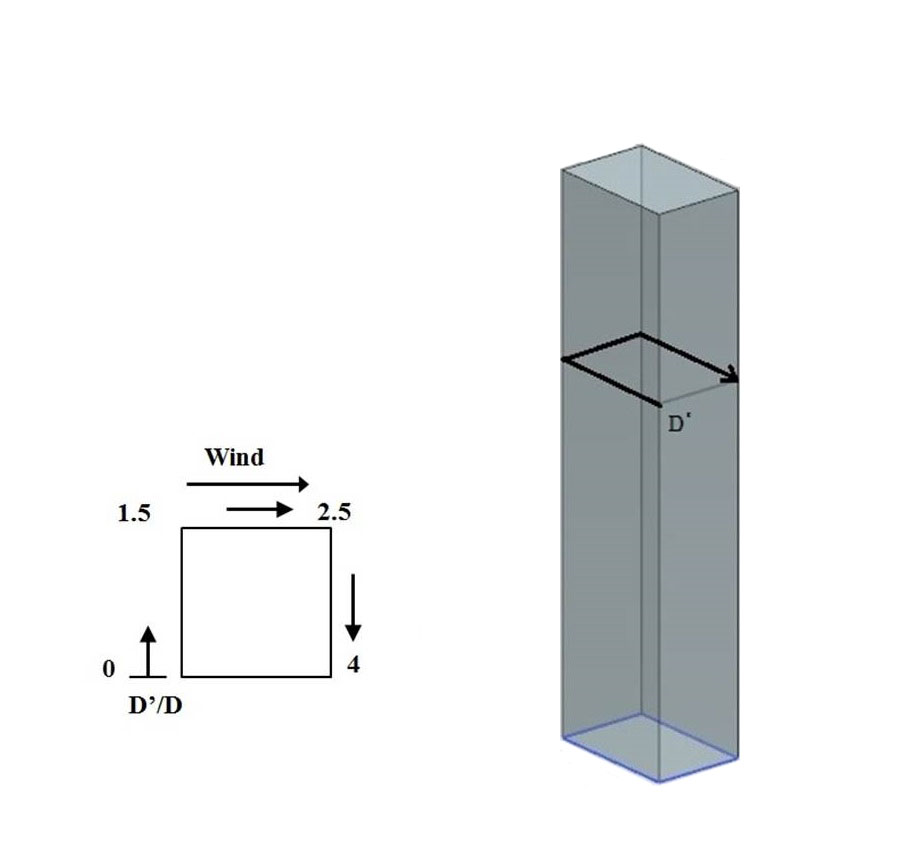
D'는 CAARC 모델의 2/3 높이에서의 부분 둘레길이를 의미하는 변수로서 Fig. 3에 나타냈다. D’를 건물 세로길이인 D로 나누어 무차원화 시켜 건물의 실제 크기에 유효한 길이비로 표현하였다.

Fig. 3. The path of D’ or D’/D through CAARC building wall.

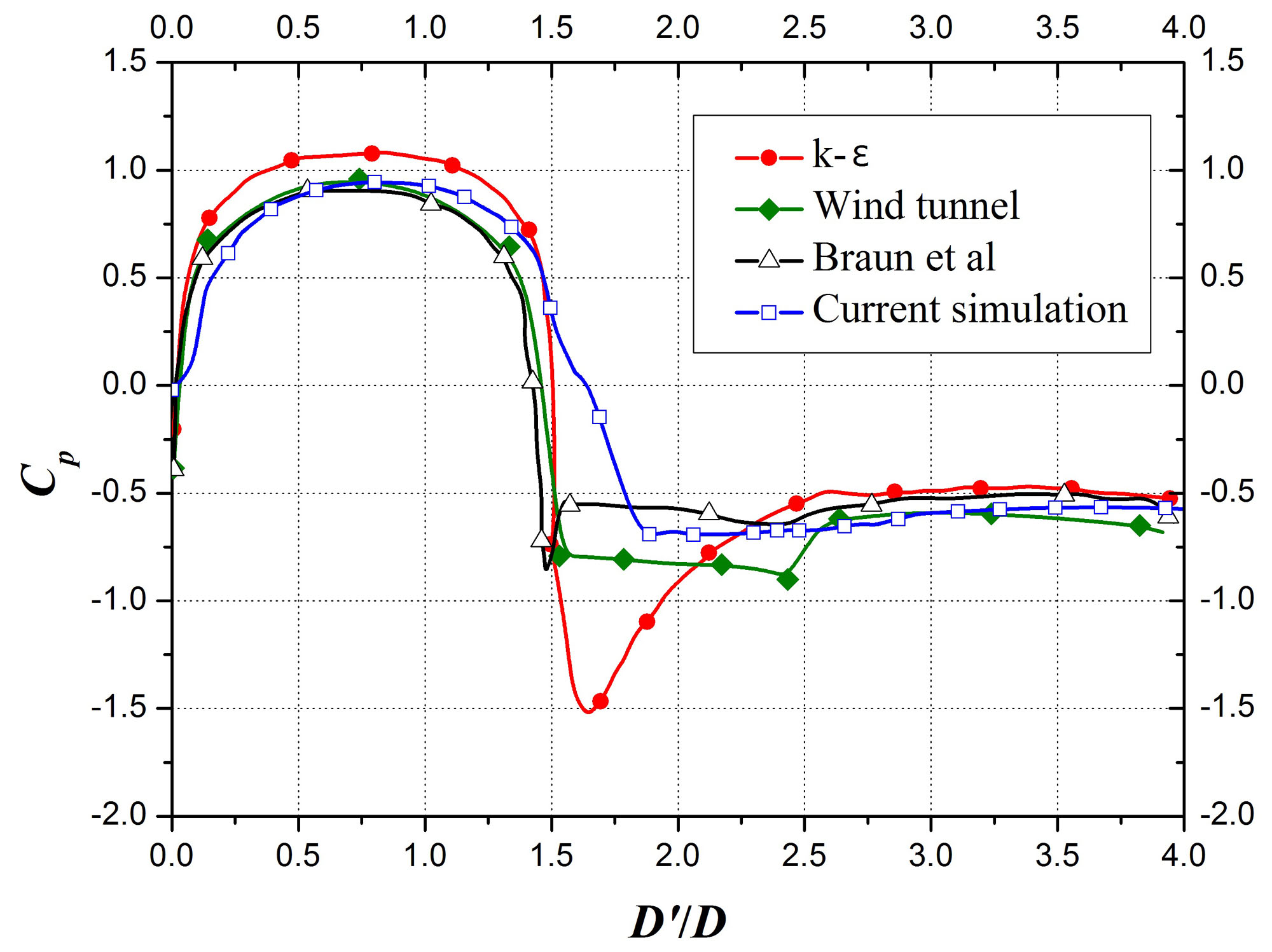
CAARC 모델 하나에 대한 풍압계수를 선행논문의 결과와 함께 Fig. 4에 나타내었다. 표준난류 모델, 격자모양, 건물조건을 같은 조건으로 적용 하였을 때 본 계산결과의 전체적인 그래프 모양은 Agerneh et al.(3)의 결과와 비슷한 것을 확인할 수 있으나 D'/D가 1.5~2.0에서 약간의 차이를 발견할 수 있다. Agerneh et al.(3)에 비하여 격자 생성을 적게 설정한 것이 차이를 발생시킨 것으로 생각 된다.

Fig. 4. Wind pressure coefficient of the CAARC model.

풍향변화에 따른 CAARC 모델의 최대 풍압계수를 해석을 통해 알아본 결과 Fig. 6과 같은 결과를 얻었다. Fig. 5에서 볼 수 있듯이 0°에서 가장 높은 풍압계수를 보였으며 45°에서 가장 낮은 풍압계수를 보였다. 0°일 경우, 풍향이 건물에 수직방향이기 때문에 건물 정면이 받는 수직방향의 속도가 가장 크므로 가장 높은 풍압계수를 나타냈다. 반면에 풍향이 45°일 때는 바람이 건물의 수직방향과 수평방향으로 분산되기 때문에 수직방향의 속도가 작아지고 따라서 풍압도 낮아져 낮은 풍압계수가 나왔다. 해석결과 0°인 경우보다 45°일 경우에 바람의 영향을 덜 받는 것을 눈으로 확인할 수 있었다.

Fig. 5. Measurements of maximum Cpover the perimeter at Z/H = 2/3.

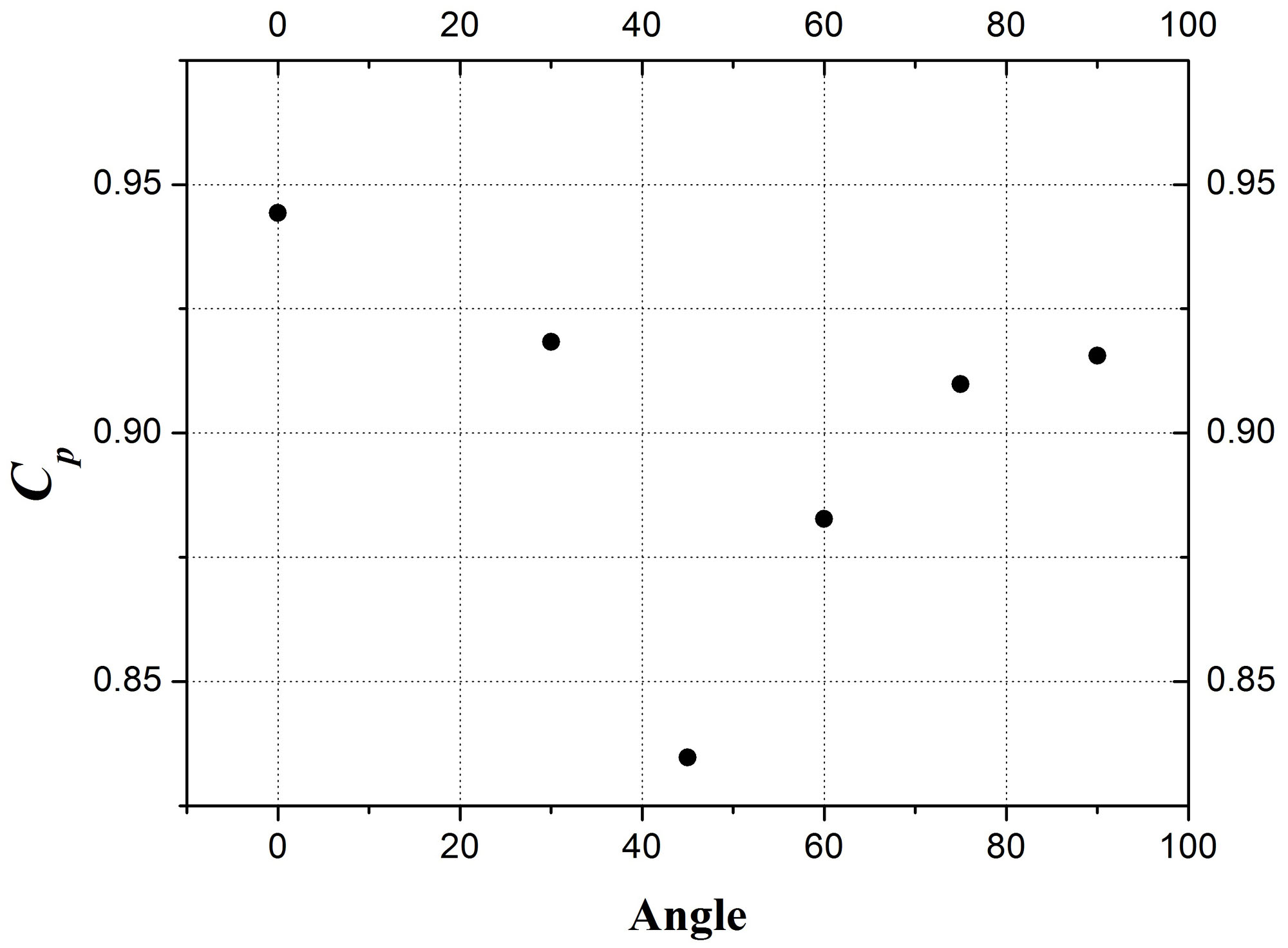
Fig. 6. Location of two buildings and the CAARC model from a top view.

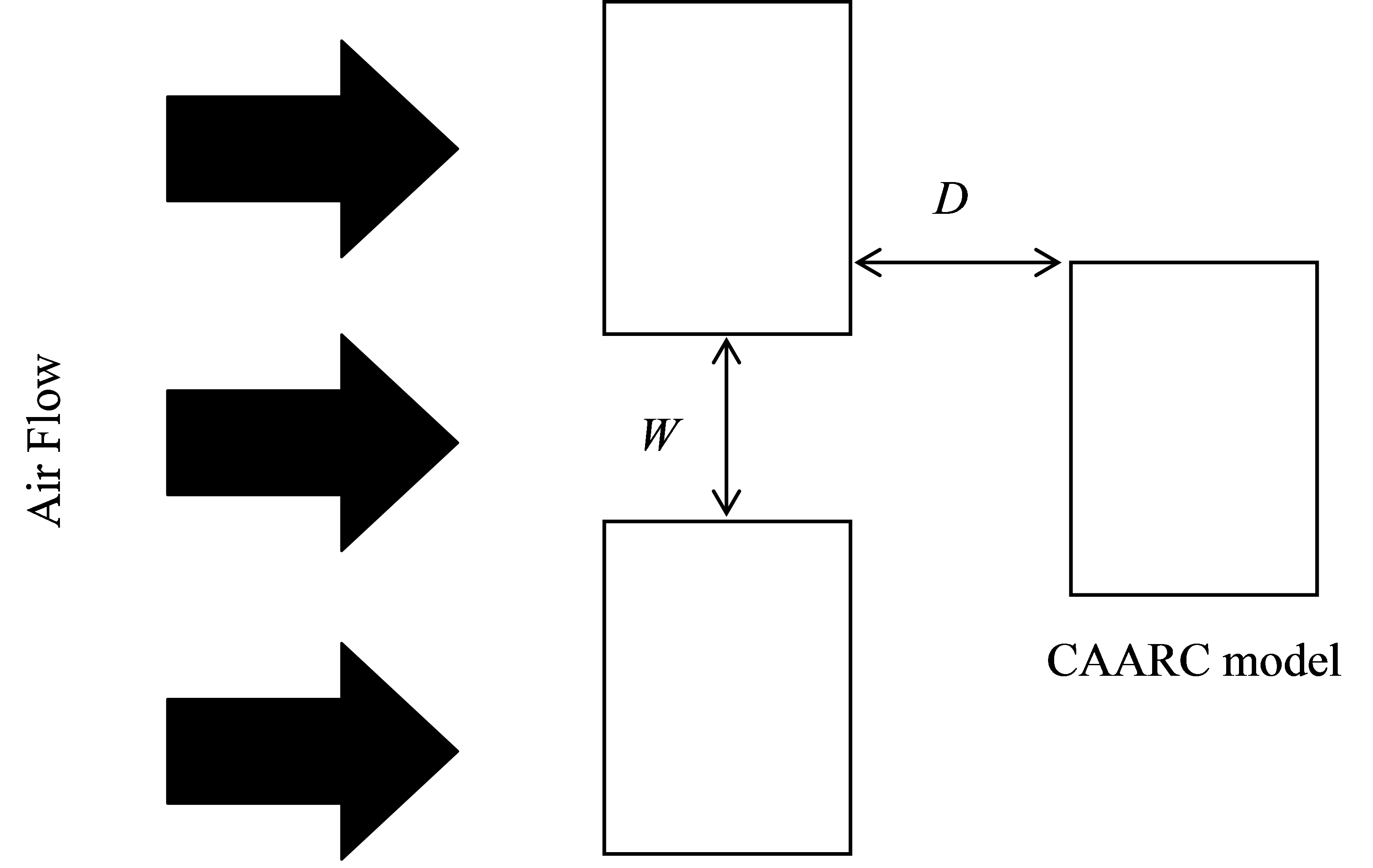
빌딩 풍의 영향을 보기 위해 CAARC 모델 앞에 1D 만큼 거리를 두고 두 건물을 위치시킨 후 그 두 건물의 사이 거리를 7 W/10, W/2, W/3, W/4로 변화시키며 CFD 해석을 수행하였다. 빌딩의 상대적인 위치에 대한 이해를 돕기 위해 모델에 대한 평면도를 Fig. 6에 나타내었다. 왼쪽 수직으로 나란히 있는 두 건물이 빌딩 풍을 생성하는 건물들이고 오른쪽에 있는 건물이 CAARC 모델이다.

Fig. 7은 앞 건물들과 CAARC 모델의 거리가 1D인 경우 빌딩 풍을 생성하는 두 건물의 사이거리가 7 W/10, W/2, W/3, W/4일 때의 최대 풍압계수를 기준 건물 앞에 빌딩이 없는 CAARC 모델의 최대 풍압계수와 비교하여 나타낸 것이다. 앞 건물들의 사이거리가 W/2이상인 경우에는 빌딩 풍에 의해 CAARC 모델이 받는 풍압이 높아졌지만 그 이하의 경우에서는 풍압이 낮아졌다.

Fig. 7. Measurements of mean Cp over the perimeter at Z/H = 2/3. The gap between two front buildings and the CAARC model is 1 D.

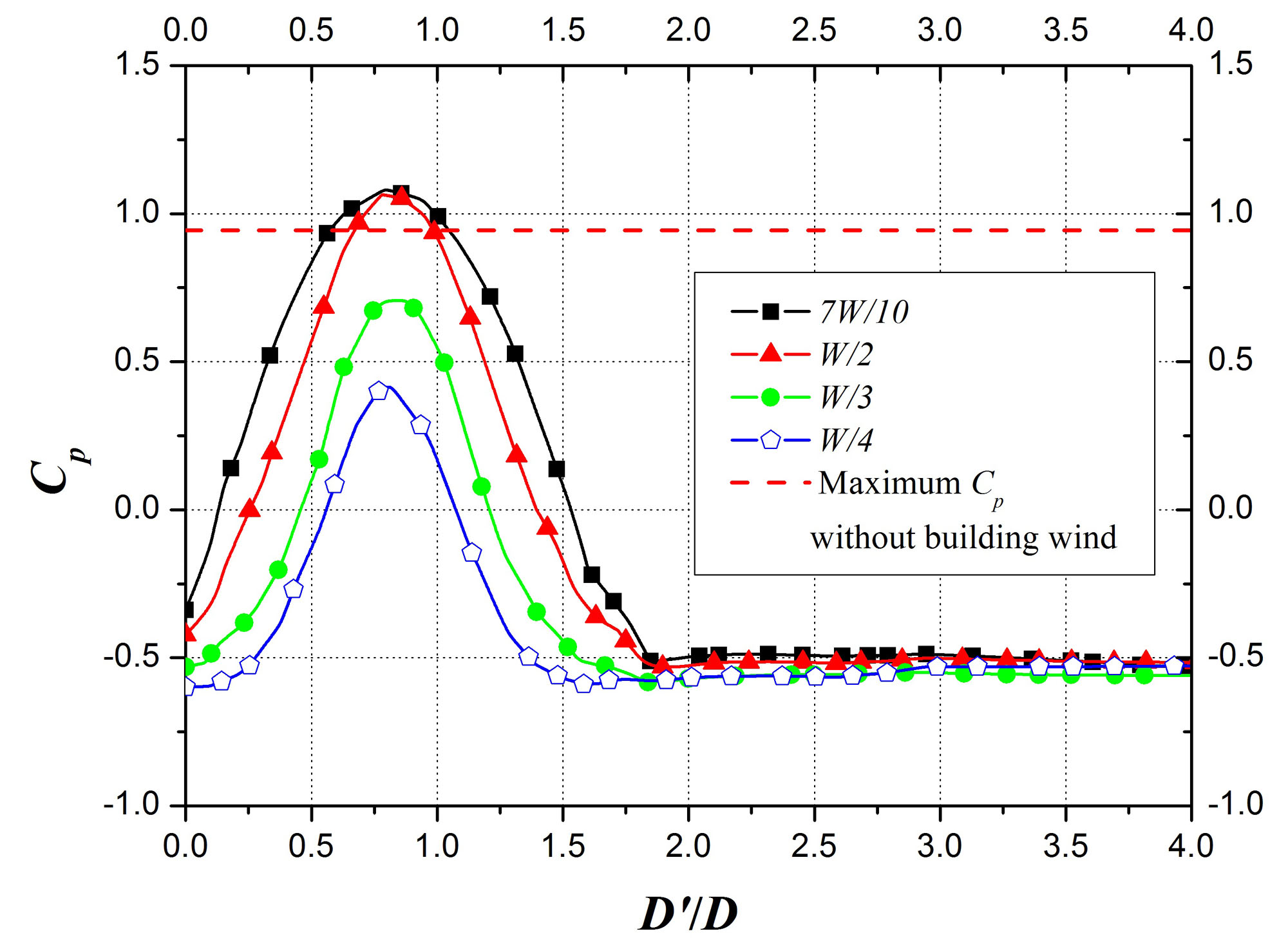
Fig. 8은 앞 건물들과 CAARC 모델의 거리가 1 D일 때와 2 D일 때 건물사이의 거리에 대해서 최대 풍압계수를 나타낸 것이다. 건물 사이의 거리가 W/3일 때 빌딩풍이 없는 경우보다 풍압계수가 더 낮아지는 것을 확인할 수 있다. 유동을 확인해본 결과 건물 사이의 거리가 W/3보다 작아지면 그 사이를 지나는 바람의 유량이 줄어들고 앞 건물의 영향을 받아 풍속이 낮아져 CAARC 모델이 받는 풍압이 감소하게 된다.

Fig. 8. Measurements of maximum Cp over the perimeter at Z/H = 2/3 with the gap between two front buildings.

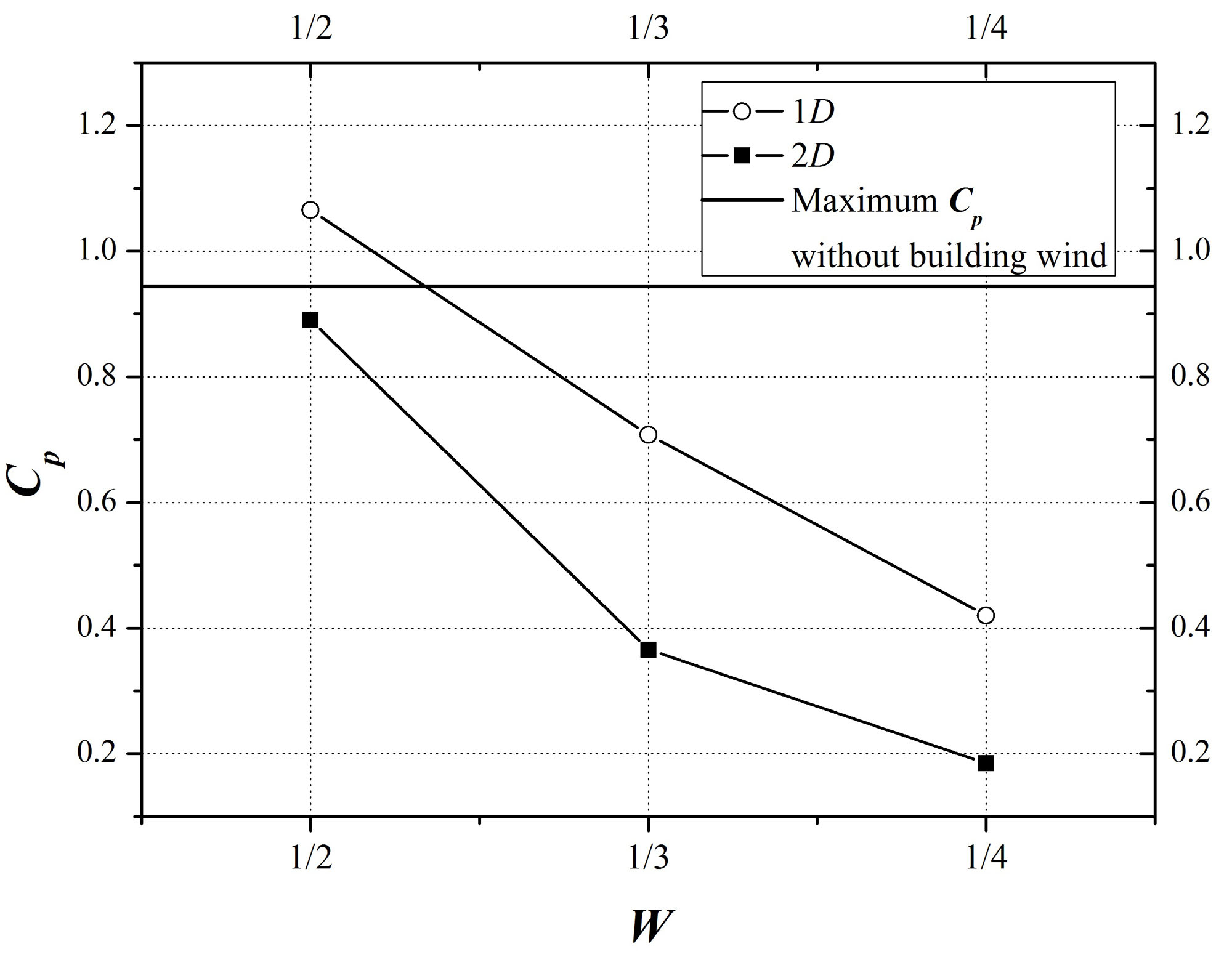
Fig. 7과 같은 조건에서 CAARC 모델과 앞 건물들과의 거리를 1 D에서 2 D로 변화시켜 해석을 해본 결과 Fig. 8과 같이 2 D의 모든 경우에서 최대 풍압계수가 빌딩풍이 없는 경우보다 낮게 나왔다. 위의 결과에서 CAARC 모델과 빌딩 풍 생성 건물들과의 거리가 2 D 이상일 때 기존 건물과 떨어져 있는 경우 빌딩 풍의 영향을 고려하지 않아도 된다는 것을 알 수 있다.

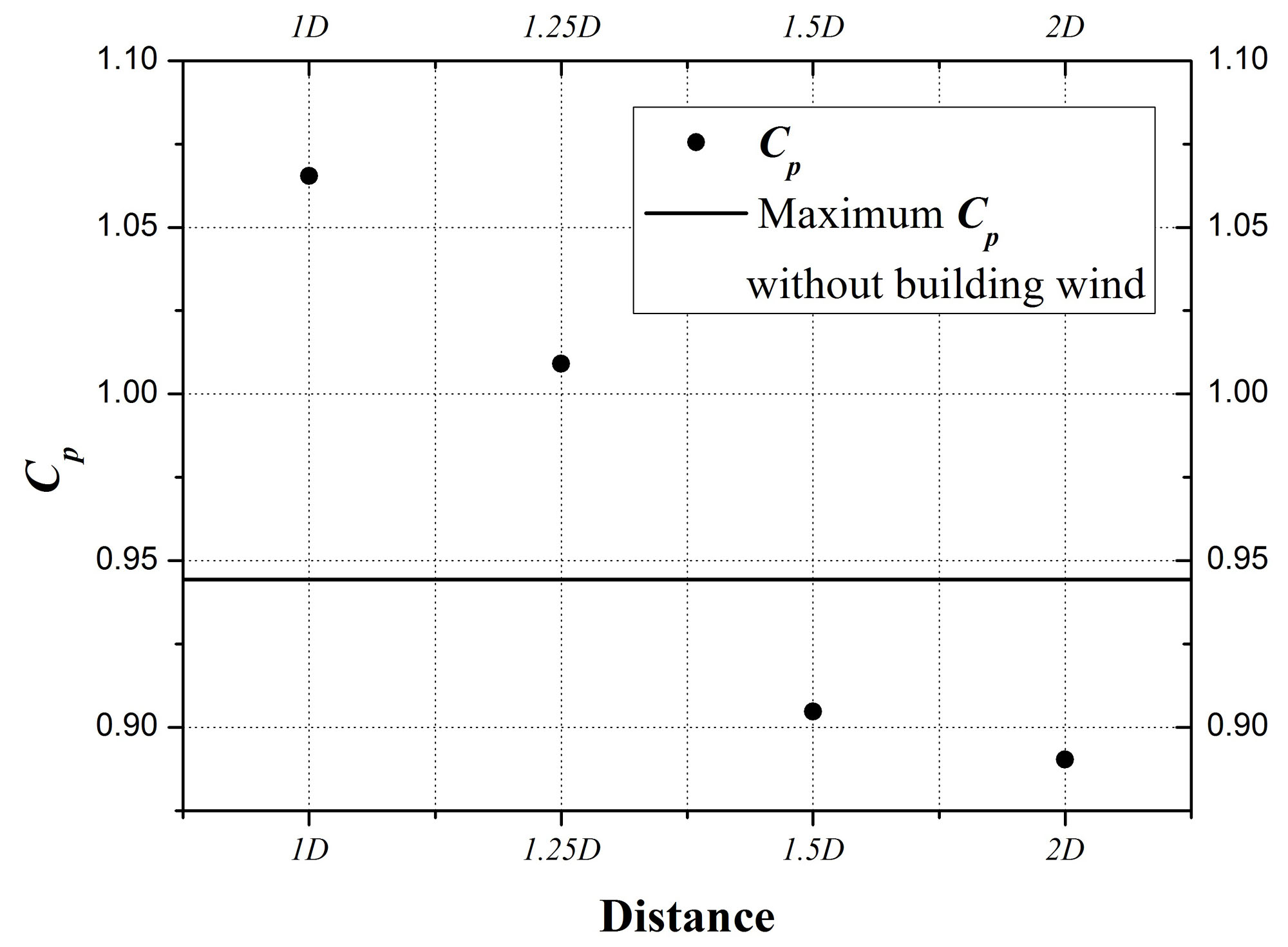
빌딩 풍 생성 두 건물의 사이거리를 CAARC 모델이 영향을 받았던 W/2로 고정한 뒤 CAARC 모델과 앞 건물들과의 거리를 2 D 이하에서 변화시켜가면서 CFD 해석을 진행한 결과 빌딩 풍의 영향을 받게 되는 거리를 찾을 수 있었다. 거리를 찾기 위해 기존에 했던 1 D와 2 D를 제외하고 차례대로 1.25 D, 1.5 D를 해석하였다. Fig. 9는 빌딩 풍을 생성시키는 두 건물의 사이가 W/2일 때 CAARC 모델과 앞 건물들 사이거리가 1 D, 1.25 D, 1.5 D, 2 D일 때의 최대 풍압계수를 빌딩 풍 없는 CAARC 모델의 최대 풍압계수와 비교하여 나타낸 것이다. Fig. 9에서 확인할 수 있듯이 CAARC 모델과 빌딩 풍 생성 건물들과의 거리가 1.25 D에서 1.5 D 사이일 때, 빌딩 풍이 없는 CAARC 모델의 최대풍압계수 값과 같은 값이 존재한다는 것을 알 수 있다. 따라서 앞 건물들과의 사이거리가 1.5 D보다 작은 경우 풍압계산에 있어서 앞 건물들과의 거리를 고려해야 된다.

Fig. 9. Measurements of maximum Cp over the perimeter at Z/H = 2/3 with the distance of the two tower and CAARC model. The gap between two buildings in front of the CAARC model is W/2.

4. 결 론

수치해석을 이용하여 CAARC 박스형 건물 주변의 유동장을 해석하고 건물외벽의 풍압계수를 구하였다. 건물풍압 분석을 위해 빌딩풍의 발생 조건을 다양하게 변화시켜 건물에 미치는 영향을 평가하였다. 이에 대한 결론은 다음과 같다.

(1) 풍향변화에 따른 해석 결과 지배적인 일정방향의 바람이 불 때 바람이 불어오는 방향에 대해 45°로 건물을 설계하는 것이 안전하다.

(2) 빌딩 풍이 있는 경우 기준 건물 앞의 두 빌딩 사이 간격이 W/2일 때 생성된 빌딩풍의 영향으로 빌딩풍이 없을 때보다 풍압계수가 높아지나 앞 건물들과 CAARC 모델의 거리가 2 D 이상이 되면 풍압계수가 낮아진다.

(3) 앞 건물들과 CAARC 모델의 거리가 1.5 D 이하가 되면 빌딩풍이 없는 경우보다 풍압계수가 높아져 빌딩풍의 영향이 기준 건물에 발생한다.

따라서 빌딩풍이 발생할 수 있는 건물 설계 시에 앞 건물들 사이거리가 W/2 이상이거나 앞 건물들과 빌딩풍의 영향을 받는 건물의 거리가 1.5 D 이내에서는 건물을 설계할 때 빌딩풍의 영향을 고려하여야한다.