2.1 판형열교환기 형상

항공기 가스 터빈엔진용 재열기는 엔진에 사용되어 토출되는 고온 저압의 가스와 연소실에 들어가게 되는 저온 고압의 공기의 열전달을 일으키는 역할을 한다. 이러한 효과는 가스터빈 사이클의 효율을 증가시키고 토출되는 가스의 온도를 낮추어 무인항공기의 비행 임무의 시간을 증가시키고 레이더가 탐지하게 힘들게 만들어준다. 이러한 열교환기는 필요효율(effectiveness)이 상당이 높아야 하므로 본 연구에서는 여러 열교환기들 중 많은 장점을 보유 한 주름진 형상이 교차(cross-corrugated)하는 판형 열교환기를 적용하여 계산하였다. Fig. 1(a)는 본 연구에서 사용된 대칭형상의 주름진 형상이 교차하는 판형 열교환기이다.

Fig. 1 Typical configuration of cross-corrugated heat exchanger using symmetric profile; (a) matrix and (b) unitary cell.

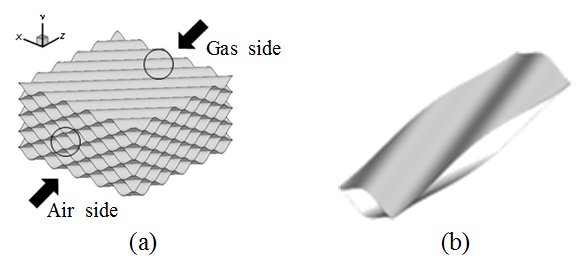
Fig. 1(b)는 판형 열교환기를 구성하는 단일 셀을 확대하여 나타낸 그림이다. 이렇게 복잡한 형상의 열교환기를 직접 full-scale로 해석을 하기 위해서는 많은 시간 및 컴퓨터 리소스등의 자원이 필요하기 때문에 본 연구에서는 1차원 열유동 네트워크 및 다공성 매질(porous media) 해석 방법을 사용하여 판형 열교환기를 해석하였다. 본 연구에서는 사용된 주름진 형상의 판형 열교환기의 전체 크기 모델에 대하여 압력강하 및 열전달 성능을 계산하고, 1차원 열유동 네트워크 프로그램 및 다공성 매질 해석 방법을 사용하여 사용된 모델들의 정확성을 비교분석하였다.

2.2 판형열교환기 기본 설계식

본 연구에서 사용된 주름진 형상의 판형 열교환기는 주름진 형상의 판을 여러장 겹치고 특수 가스켓으로 유체가 옆으로 새어나가지 못하게 만든 열교환기로 유체들이 물리적인 접촉 없이 주름형상의 판을 사이에 두고 고온과 저온의 유체가 대향 유동으로 흐르며 열을 전달한다. 본 연구에서 사용한 지배방정식들은 다음과 같다.

여기서 ui, p, T는 각각 i-방향의 속도, 압력, 온도를 나타내고, ρ, μ, Cp 그리고 k는 각각 유체의 밀도, 점성계수, 비열, 열전달계수를 나타낸다. 식(1) 식(2) 식(3)은 비압축성의 Reynolds-averaged Navier Stokes(RANS) 방정식으로 모든 변수들은 시간 평균한 값을 사용한다. 상용 코드인 FLUENT를 이용하여 본 연구의 수치 계산을 진행하였으며, 난류 모델은 Low-Reynolds number k-ε 모델을 사용하였다. 운동량과 에너지 수송식의 공간 이산화를 위하여 2차 풍상차분법을 사용하였다. 본 연구에서 사용되어진 변수는 다음과 같다. 수력 직경 D_h는 다음과 같이 나타낼 수 있다.

여기서 V는 단일 셀의 부피, A_w는 단일 셀의 위아래 벽면 넓이를 의미한다. 유동의 평균 속도는 식(5)와 같다.

여기서 Γ는 질량 유량, A_inlet는 단일 셀의 입구 면적을 의미한다. 이와 같은 변수들을 이용하여 다음과 같이 Reynolds 수를 정의 할 수 있다.

그리고 Fanning friction factor는 다음과 같다.

여기서 L은 Fig. 1(b) 단일 셀에서의 유동 길이를 나타낸다. 다른 무차원 수들인 Nusselt 수, Stanton 수, Colburn j-factor는 다음과 같이 정의 할 수 있다.

Fanning friction factor(f)와 Nusselt 수(Nu)는 CFD 계산을 통한 단일 셀로부터 계산되어지고, 최소 제곱법을 이용한 2차 다항식의 Re에 관한 함수로 표현 된다.

2.3 1차원 열유동 네트워크 해석 이론

Kim et al.(10)은 정확한 마찰 계수값을 주어 복잡한 유동을 보다 간소화 시켜 해석하는 1차원 열유동 네트워크를 개발하였다. Fig. 2(a)와 Fig. 2(b)는 대향유동의 gas side와 air side의 네트워크 구성도를 보여준다. 여기서 점으로 표시된 것은 노드(node)로 unit cell을 나타내고, 각각의 노드를 연결하는 화살표는 유체의 유동경로로 가지(branch)를 나타낸다. 1차원 열유동 네트워크는 각각의 노드를 통하여 유동의 출입이 결정되고, 선으로 나타난 가지에서 각 노드를 통해 지나가는 유체의 압력과 온도가 변하게 된다. Gas side의 경우 전체적인 유동의 흐름은 좌측에서 우측으로 흘러가고 좌측의 1번 노드에서 시작하여 우측의 26번 노드를 통과하는 형태로 표현되고, Air side의 경우 우측에서 좌측으로 유동이 흐르며 노드 번호는 우측의 1번 노드에서 시작하여 좌측의 26번 노드를 통과하는 형태로 나타난다. 1번 노드와 26번 노드는 입․출구의 매니폴드(manifold)를 나타낸다. 본 연구에서는 균일한 분포를 가지는 매니폴드로 가정했다. 각가의 토폴로지는 하나의 층(Layer)을 이루게 되며 네트워크를 구성하게 되는 가지들은 각각 대향유동으로 구성하게 된다. 예를 들어 Fig. 2에서 Gas side의 가지 B4와 Air side의 가지 B34는 대향유동을 의미한다. 열교환기 전체의 열전달 계산에서 대향유동의 ε-NTU 관계식은 아래와 같이 나타 낼 수 있다.

Fig. 2 1-D network topology for counter-flow arrangement; (a) gas side and (b) air side.

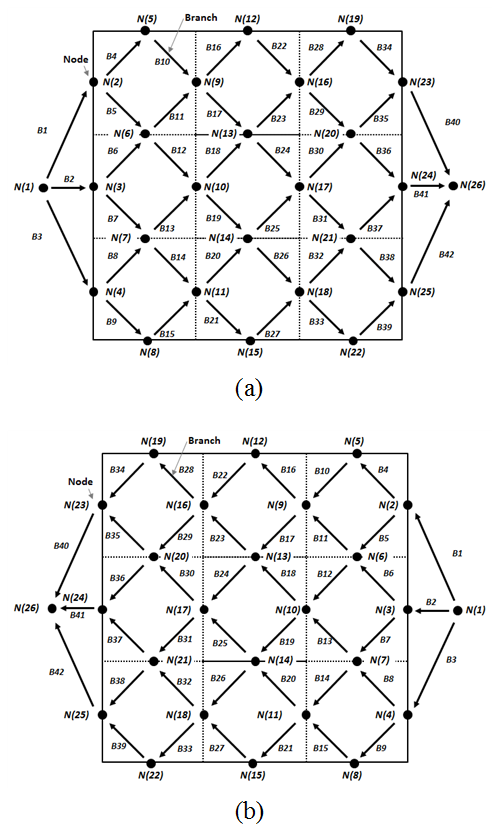
여기서 C*와 NTU는 각각 열용량비와 전달 단위수를 의미한다.

여기서 U는 총괄 열전달계수를 A는 열전달 면적을 나타낸다.

Gas side와 Air side의 압력 차이는 다음과 같은 식으로 구하며 L은 unit cell의 유동 길이를 나타낸다.

Kirchhoff 법칙으로 에너지 및 질량유량 평형을 유지하는 것을 확인하고 뉴튼-랩손 반복법을 사용하여 계산을 수렴시킨다. 먼저 CFD 계산등을 통하여 unit cell의 Fanning friction factor와 Nusselt 수를 구한 후 이 값들을 상관식의 형태로 각 가지에 적용하며 유체의 물성치는 두 개의 노드를 연결하는 가지에서 평균 온도를 사용하여 계산한다.

2.4 다공성 매질 해석 방법

다공성 매질 해석 방법은 상용 프로그램인 FLUENT를 사용하여 해석하였으며, FLUENT 프로그램에서 사용된 수식은 다음과 같다.

여기서 S는 I방향의 운동량 방정식에 대한 생성항이며, α는 삼투성, C₂는 관성저항을 나타낸다. 식(15)는 간편화된 운동량 방정식에서 압력강하와 생성항의 비교를 나타낸 식으로 이는 압력강화를 생성항과 다공성 매질의 두께의 곱으로 나타낼 수 있다. 다공성 매질 해석의 식은 층류에서는 C₂를 0으로 가정하기 때문에 다음의 Darcy’s law와 같아진다.

반면 고속의 유동일 때는 C₂가 관성손실을 보정하는 역할을 한다. 이 상수는 유동 흐름방향의 단위길이 당 손실계수로 볼 수 있기 때문에 압력강하를 동압수두의 함수로 나타낼 수 있다. 실험 또는 계산으로 얻어진 속도와 압력강하 자료를 통하여 삼투성을 나타내는 α와 관성저항을 나타내는 C₂를 구하게 된다.

식(17)은 최소제곱법을 이용하여 평행한 두 평판 사이의 압력강하 근사식을 나타낸 것이다. 얻어낸 압력강하와 속도를 식(17)과 같이 나타내고 여기서 계수 A와 B를 구해낸다. 상수 A와 B를 구하고 난 후 식(17)을 식(16)과 비교하여 α와 C₂를 구한다.

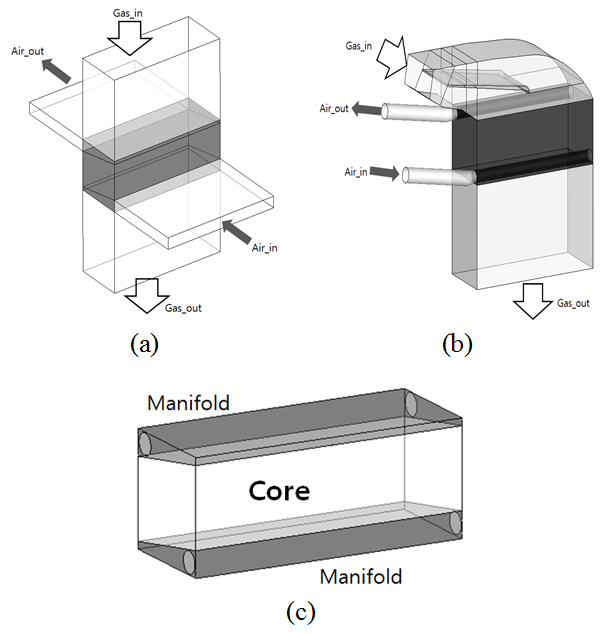
본 연구에서는 1차원 열유동 네트워크 프로그램을 사용한 결과와 비교 및 검증하기 위하여 다공성 매질 수치 모델 결과를 이용하였다. Fig. 3는 본 연구에서 다공성 매질 모델을 사용하여 해석한 두 모델의 개념도이다. 기본적으로 두 모델 다 중간 부분에 열교환기가 위치하고, 열교환기는 두 가지의 유체가 역류하며 열교환이 이루어지는 코어(core) 부분 및 코어 양 옆에서 직교로 열교환이 이루어지는 매니폴드(manifold)로 나누어 진다. Fig. 3(a)는 기존의 열교환기의 입출구 형상 및 유로를 간소화 하여 만든 모델이고 Fig. 3(b)는 판형열 교환기의 세부사항을 모두 포함하는 전체 모델으로 입출구의 형상 변화 및 복잡한 가이드 베인 형상등을 포함하고 있다. 두 모델의 계산 결과를 직접 비교하기 위하여 단순화 된 모델과 전체 모델의 열교환기 치수를 같게 적용하였다. 계산시간이 작은 간소화 된 모델을 이용하여 1차원 열유동 네트워크 프로그램과 결과 값을 비교하고 최종적으로 전체 모델과 1차원 열유동 네트워크 프로그램을 비교함으로써 1차원 열유동 네트워크 프로그램의 정확성과 사용 범위를 파악하였다.

Fig. 3 Schematics of the 3D porous media model; (a) simplified model, (b) full model and (c) heat exchanger core with manifolds.

2.5 판형열교환기 작동 조건

본 연구에서 사용된 주요 작동조건은 Table 1과 같다.

3.1 해석 방법 검증

Table 2는 본 연구에서 이용된 네트워크 프로그램과 선행연구(8)의 실험결과를 비교 및 검증한 결과이다. 본 연구에서 사용되어진 1차원 네트워크 프로그램과 선행연구(8)에서 실험값과 비교해 봤을 때 압력차의 상대오차가 8.1% 이하로 차이가 나는 것을 알 수 있었다. 단순화 된 CFD 상관식을 고려할 때 이 차이는 동의할 만 수준이다.

3.2 해석 방법에 따른 압력강하 비교

Fig. 4(a)~Fig. 4(d)는 공기와 가스가 열교환기를 통과하면서 생기는 압력강하 컨투어(contour)를 간편화된 모델과 전체 모델에 대하여 나타낸 것이다. 이 그래프는 열교환기의 정 중앙의 단면도에서 얻은 데이터를 바탕으로 만들어졌다. 공기의 경우 간편화된 모델에서는 우측 아랫 방향에서 좌측 윗편으로 유동이 흐르고, 전체 모델에서는 우측 아래에 위치한 원으로 흘러 나온 후 왼쪽 윗편에 위치한 원으로 들어가도록 설계되어 있다. 또한 Fig. 3에서 볼 수 있듯이, 간편화 된 모델의 경우 공기가 넓은 면적을 통하여 매니폴드에 골고루 들어가는 반면 전체 모델에서는 좁은 입구를 통하여 들어가기 때문에 유체가 매니폴드에 균일하게 들어가지 못하게 되고 유동이 꺾이게 되는 횟수 또한 차이가 나게된다. 이러한 유로의 영향은 유선을 나타내는 Fig. 5(a)~ Fig. 5(d)를 통하여 확인 할 수 있다. 언급한 유로의 형상차이로 인하여 공기의 경우 간편화 된 모델과 전체 모델의 압력강하 값의 차이가 크게 나는 것을 알 수 있다. 이는 Fig. 4(a)와 Fig. 4(b)의 비교를 통하여 확인 할 수 있다. 가스의 경우 간편화 된 모델에서는 유로가 수직으로 형성되어 간단한 반면, 전체 모델에서는 입구를 통하여 들어온 유체가 안내 날개를 지나 출구로 향하게 된다. 또한 열교환기 내부에서는 원형 파이프가 존재하여 가스 유동에 영향을 미치게 되고 이는 Fig. 4(c)와 Fig. 4(d)에 명확하게 나타나 있다.

Fig. 4 Pressure drop along the heat exchanger (a) air side simplified model, (b) air side full model, (c) gas side simplified model, and (d) gas side full model.

Fig. 5 Pathline along the heat exchanger (a) air side simplified model, (b) air side full model, (c) gas side simplified model, and (d) gas side full model.

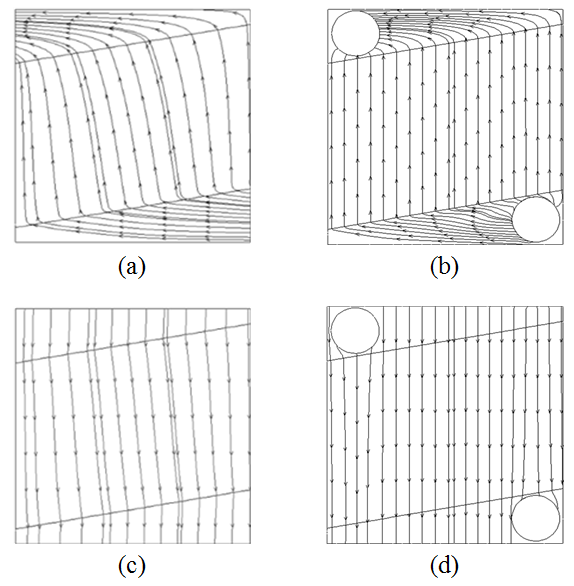
Fig. 6 Temperature distribution contour along the heat exchanger (a) air side simplified model, (b) air side full model, (c) gas side simplified model, and (d) gas side full model.

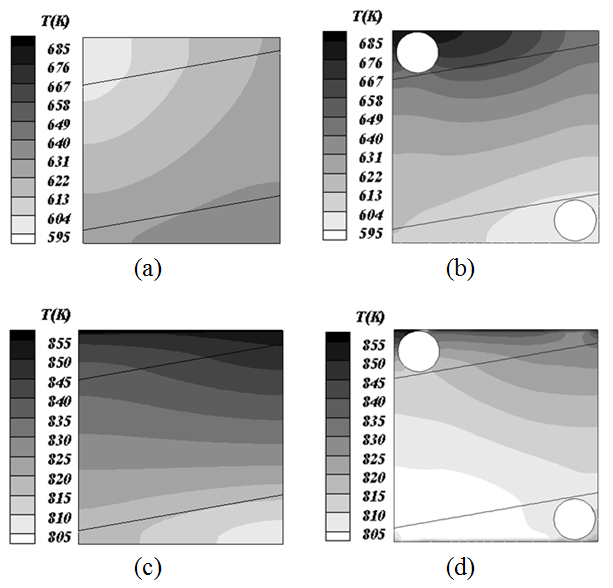
Fig. 7 Comparison of performance between 1D network, CFD-simplified and CFD-full model of the heat exchanger：(a) pressure drop in air-side,(b) pressure drop in gas-side, and (c) heat transfer rate.

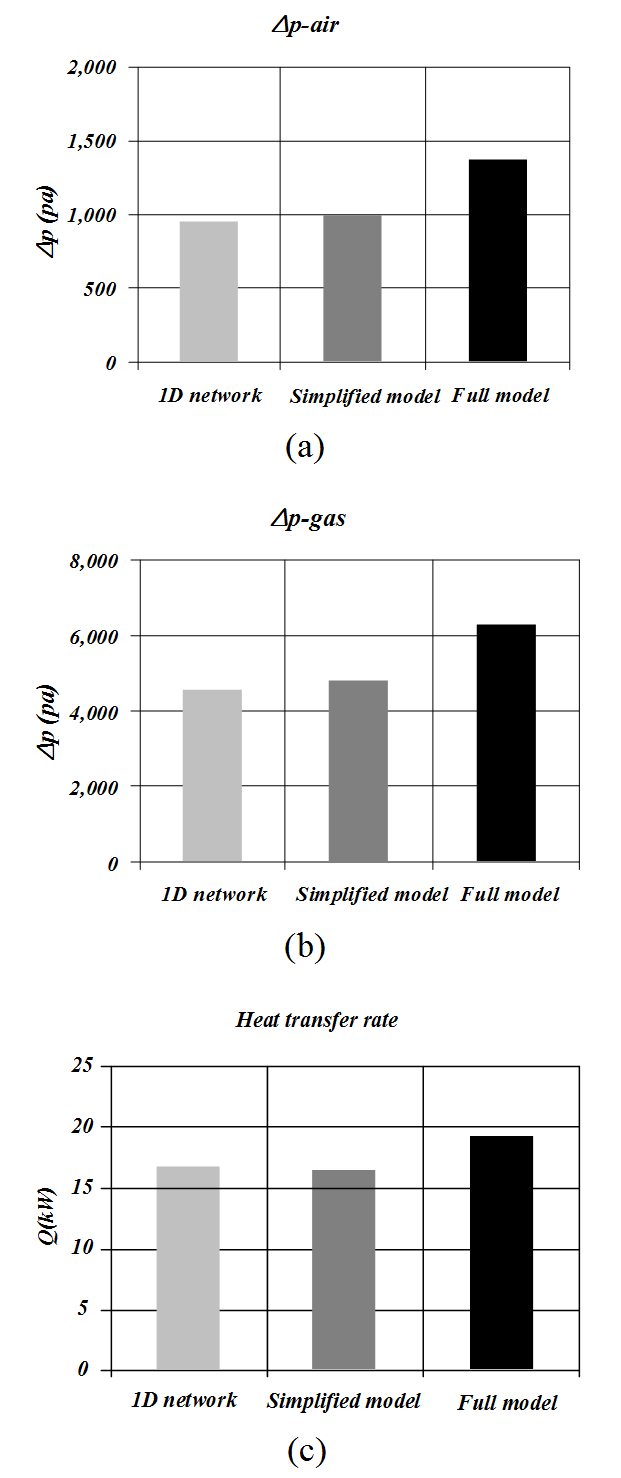
Fig. 7(a)～Fig. 7(b)는 해석 방법에 따른 공기, 가스의 압력강하를 비교한 그래프 이다. 그래프에서 볼 수 있듯이 1차원 네트워크 프로그램을 통하여 얻은 계산 결과는 다공성 매질을 사용하여 해석한 간소화 된 모델의 계산 결과와 비슷한 것을 알 수 있다. 하지만 앞의 두 모델의 경우 전체 모델(full model)을 3 D 해석 한 결과와 큰 차이를 보인다. 이는 전체 모델의 경우 복잡한 형상들이 유체의 흐름에 영향을 많이 미치기 때문으로 파악된다.

3.3 해석 방법에 따른 열전달 비교

Fig. 6(a)~Fig. 6(d)는 열교환기 내부에서 공기와 가스의 온도 분포도를 간편화된 모델과 전체 모델에 대하여 나타낸 것이다. 공기의 경우 간편화된 모델과 전체 모델의 사이에서 온도분포의 경향성에는 큰 변화가 나타나지 않는 것을 확인 할 수 있다. 하지만 가스의 경우 간편화된 모델에서는 저온의 가스가 열교환기 우측 벽면에 위치하였던 반면, 전체 모델에서는 원형 파이프의 존재로 인하여 저온의 가스가 열교환기 좌측에 위치하는 것을 확인 할 수 있다. 그리고 Fig. 6(d)에서 열교환기 상부에 급격한 온도 변화가 일어나는데 이는 고온의 가스가 열교환기에 유입되자마자 열교환이 활발하게 일어난다는 것을 의미한다. 이러한 온도차이로 인하여 전체 모델에서 열교환기의 열전달 량은 간편화된 모델에서의 열전달 량보다 높은 것을 유추 할 수 있다. Fig. 7(c)는 해석 방법에 따른 열교환기의 열전달 량을 비교한 그래프이다. 압력강하의 차이와 마찬가지로 1차원 네트워크 모델의 결과와 다공성 매질 해석을 사용한 간편화된 모델의 경우 값의 차이는 약 1.5%로 매우 근사한 값을 보여준다. 하지만 다공성 매질 해석을 사용한 전체 모델과 간편화된 모델은 17.5%의 비교적 큰 차이를 나타낸다. 전체 모델과 간편화된 모델사이에 열전달 면적의 차이가 없기 때문에, 앞서 비교분석한 압력강하 값의 차이와 온도 분포도의 차이로 설명이 가능하다. 전체 모델의 경우 간편화된 모델에 비하여 형상손실이 더 크고 그 때문에 열교환기 내부 유동속도가 간편화된 모델에 비하여 더 커진다. 따라서 증가된 유동속도는 열전달 계수에 영향을 미치고 이는 다시 전체 열전달 양에 영향을 미치게 된다. 전체 모델에 존재하는 원형 파이프의 영향으로 가스의 유동방향이 바뀌게 되어 생기는 온도차이로 인하여 열전달 량이 차이가 나게 된다.