1. 서론

최근 전 세계적으로 효율적인 에너지 소모에 대한 중요성이 부각되고 있다. 이와 같은 추세에 따라 건물에너지 소비에 관한 문제가 대두되면서 정부 또한 2010년 1월 이후 부터 건물에너지 효율등급 취득을 추진하여 유지, 관리 비용을 절감시키도록 유도하고 있다.(1) 건물 설계 시 배관의 선정은 건물 에너지 비용의 큰 부분을 차지하는 펌프의 동력비용과 직결된다.

배관들은 냉방공조 시스템의 냉매나 냉온수 등 다양한 종류의 유체를 운반하는 역할을 하게 되는데 유체를 운반하기 위해 펌프의 동력을 이용하게 된다. 유체를 운반하는 과정 중에 배관과 유체사이에 작용하는 마찰력으로 인하여 유체를 이동시키는데 방해를 받게 된다. 만약 설계자가 배관의 직경을 작게 설계한다면 배관의 단면적이 좁아지고 그에 따라 유속이 빨라지면서 마찰저항 값이 더 상승하게 된다. 이는 사용해야하는 펌프의 동력이 더 높아져야하고 이에 따라 운전비용이 상승하게 되나 배관의 직경이 작아지면 배관단가가 낮아지므로 초기 투자 비용이 낮아진다. 이와 같이 배관의 최적 직경설정과 펌프의 운전비용의 최적조건은 서로 상반되는 요구사항이므로 어떤 마찰저항 값에서 가장 경제적인 설계가 되는지 분석해볼 필요가 있다. 현재 경제적인 배관을 선택하는 데에는 설계자의 직감에 의존하고 있고 연구도 거의 진행되지 않고 있다.

현재까지의 연구동향을 살펴보면 Choi(2)는 배관을 설계 할 때 고려해야 할 사항을 살펴보고 배관 크기를 선정하는 방법론에 대하여 기술하였다. 하지만 경제적인 관점에서의 배관 크기 선정 및 과거에 비해 에너지비용의 변화에 따른 자세한 연구는 매우 미미하다.

본 연구에서는 냉각수를 운반하는데 사용하는 배관에 대하여 10년간 운전한다는 가정 하에 배관 초기투자비와 펌프 운전비가 최상의 경제성을 가질 수 있는 최적의 단위마찰저항 값을 고찰하고자 한다. 단, 각 비용의 단순 비교를 위해 이자는 고려하지 않았다.

이를 위해 연구 대상을 설정하고 대상에 대한 순간최대유량, 전양정을 구하기 위한 배관길이, 배관비용 등 기본적 Input-data를 결정하고 작동유체에 맞는 배관종류를 선정한다. 그 후 단위마찰저항 값을 변화시키며 Hazen-Williams 식으로 배관직경을 결정한다. 펌프 선정을 위한 건물의 전양정을 구하고 펌프 선정을 하고 축동력을 구하여 펌프 운전비용을 계산한다. 마지막으로 펌프 운전비용 및 초기투자비(배관단가, 공사비)를 합산하여 가장 경제적인 단위마찰저항 값을 도출 하여 현재 기준이 되는 30 mmAq/m 단위마찰저항 값에 따른 총 비용과 비교할 것이다. 위의 일련의 과정을 Fig. 1의 Flow chart를 통하여 나타내었다.

Fig. 1 Flow chart of the cycle simulation.

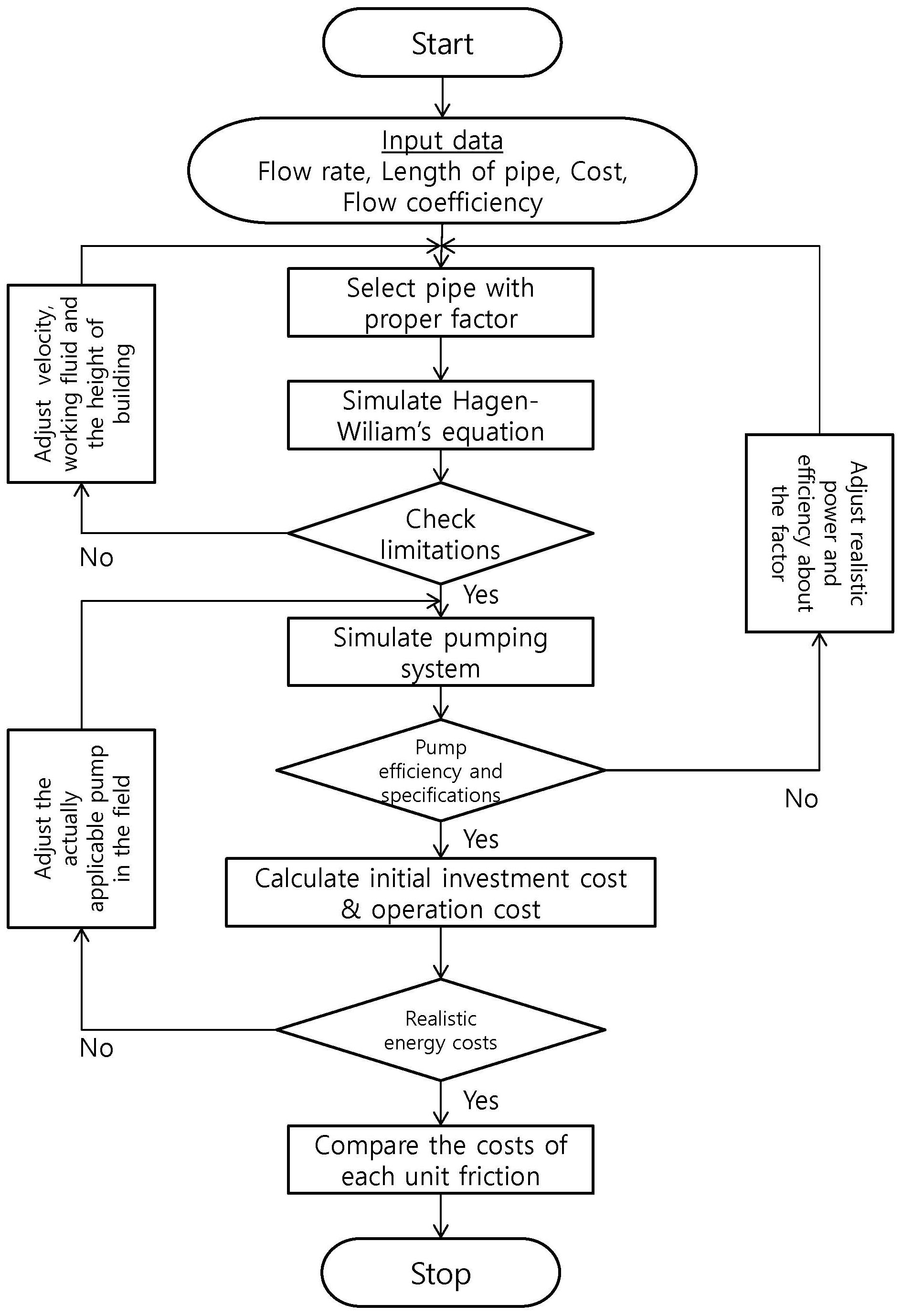
2. 경제성 해석 과정

2.2 전양정계산 및 펌프선정

펌프를 선정하기 위해 건물의 전양정을 구해야 한다. 전양정이란 펌프가 냉각수를 순환시키기 위해 필요한 실제 펌프의 양정 높이를 말하며 다음 식(1)와 같이 크게 4개 사항에 의하여 결정된다.

(1)

$$H=(H_a+H_m+H_l+H_r)\times \alpha$$

(2)

$$H_m=i\times L$$

(3)

$$H_l=H_m\times 0.5$$

H_α(실양정)은 냉각수 탑의 높이로 5.5 m, H_m(주손실 수두)는 배관의 단위마찰저항 값과 총 길이를 곱하여 구할 수 있고, H_l(부차손실 수두)는 일반적으로 주손실 수두의 50%로 계산한다. H_r(냉동기 손실수두)는 25층 건물의 장비일람표(3)를 참고했으며 그 외 압축기, 열교환기, 팽창밸브 등의 기계적 손실을 합한 값이다. 본 논문에서 해석하는 건물에서는 단위마찰저항 값이 30 mmAq/m라 선정한 경우, 주손실 수두는 10.5 m, 부손실 수두는 5.25 m로 계산되었고 냉동기 손실수두는 3.73 m로 설정 하였고 α(여유율)은 1.1로 설정하였다.

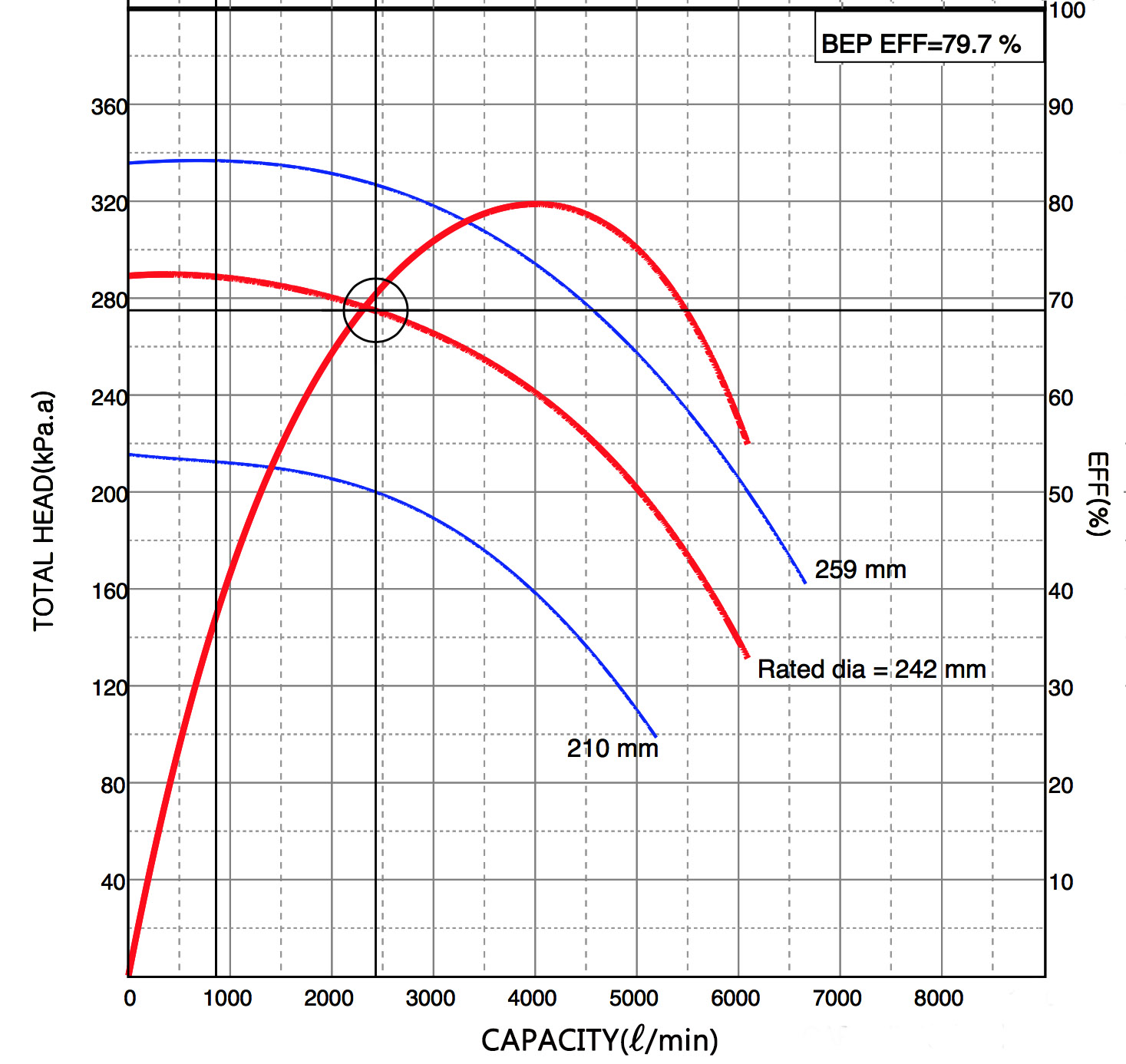
펌프선정을 위하여 효성 굿스프링스 프로그램을 사용하였다. 효성 굿스프링스 프로그램은 사용자가 펌프의 전양정과 유량을 대입하면 최대효율을 발휘하는 펌프모델을 선정해주는 프로그램이다. Table 1는 효성 굿스프링스 프로그램에 구해진 양정량과 순간최대 유량을 입력하였을 때 나온 사용가능 펌프를 나타낸 표이고, Fig. 2은 한 펌프의 전양정과 효율을 순간최대 유량에 대해 나타낸 펌프성능 곡선이다. A효율은 해당 펌프가 발휘 할 수 있는 최대의 효율로서 Fig. 2의 포물선 곡선의 최대값이고 효율은 사용자가 입력한 Input값에서 발휘할 수 있는 효율을 나타낸다. Table 1에서 B효율이 가장 높은 펌프를 선정하면, 해당하는 축동력과 효율을 알 수 있다. 원으로 표시된 교점은 입력된 유량과 전양정의 교점이며 우측 y축에서 이에 대한 효율을 확인할 수 있다. Fig. 2에서 주어진 전양정 27.5 m와 최대유량 2,432 l/min에 해당하는 B효율을 구하면 원으로 표시된 70.4%가 된다.

Table 1 Pump models by Hyosung goodsprings program

Model	A efficiency (%)	B efficiency (%)	Motor power (kW)	Shaft power (kW)
iLP 150～250	216.2	21.7	22	15.9
iLP 100～315	206.7	24.5	22	19.1
iLP 200～250	199.3	27.5	30	24.1

Fig. 2 Efficiency curve for iLP 150～200 (30 mmAq/m).

3. 결과 및 고찰

단위마찰저항의 변화가 작은 경우 Hazen-Williams 식을 통해 변화된 직경을 구하더라도 배관의 직경의 규격이 이미 정해져 있기 때문에 실제로 그 직경의 배관이 존재하지 않을 수 있다. 따라서 같은 규격 내에서도 단위마찰저항 값이 다른 배관이 존재한다고 가정 한 후 계산을 진행하였다.

Table 3는 단위마찰저항 값을 5 mmAq/m 간격으로 변화시켜 가면서 배관직경, 펌프 양정량, 규격, 축동력의 계산 결과를 나타낸 표이다. 총 비용의 차이를 확연하게 나타내기 위하여 1 mmAq/m 간격이 아닌 5 mmAq/m 간격으로 설정하였다. 각각의 단위마찰저항 값에 따라 전양정을 구하고 Hazen-Williams 식을 통해 직경을 구해서 직경보다 한 치수 큰 규격을 선택하였다. 그리고 각 단위마찰저항 값에 따르는 각기 다른 펌프의 축동력을 이용하여 연간소모동력을 계산하였다. 운전은 하루 10시간, 한 달중 22일, 1년 중 365일 하는 것으로 가정했다. 이렇게 계산된 펌프의 연간소모동력으로 부터 한국전력의 계절별, 시간별 전기비용을 참고하여 연간펌프구동비용을 계산하여 Table 4에 나타내었다.

위의 축동력계산의 오류여부를 확인해보기 위해 효성굿스프링스 프로그램과 손계산의 축동력 결과 값을 Table 5에 비교하였다. 축동력에 대한 계산식은 다음과 같이 식(5)으로 나타낼 수 있다. $\gamma$, Q, H는 각각 비중량, 토출량, 전양정을 의미하며 η는 제 2.2절에서 구한 펌프의 B 효율이다.

계산 결과 오차값은 1% 미만으로 손계산에 대한 프로그램의 결과가 거의 일치하였다.

Fig. 3는 각 단위마찰저항 값에 대한 1년 간의 펌프구동비용과 배관의 초기설치비용을 나타낸 것이다. 20, 25 mmAq/m의 경우에는 250 A의 규격 30, 35, 40 mmAq/m는 200A의 규격으로 계산이 되었기 때문에 20, 25 mmAq/m의 초기설치 비용이 같고 30, 35, 40 mmAq/m의 초기설치비용이 같은 것을 확인할 수 있다. 그리고 마찰저항이 커질수록 펌프의 동력이 커지기 때문에 펌프 구동비용도 상승한다. 20, 25 mmAq/m는 초기비용이 높은 것에 비해 펌프 구동비용이 적게 소비되고, 나머지 마찰저항 값에서는 초기비용이 비교적 낮지만 펌프구동비용의 소비가 많은 것을 볼 수 있다. 마찰저항 값에 따른 경제성 분석을 위해 총 비용 그래프를 통한 분석이 필요하다.

Fig. 3 Comparison of the initial investment and operation cost per year with friction factor unit.

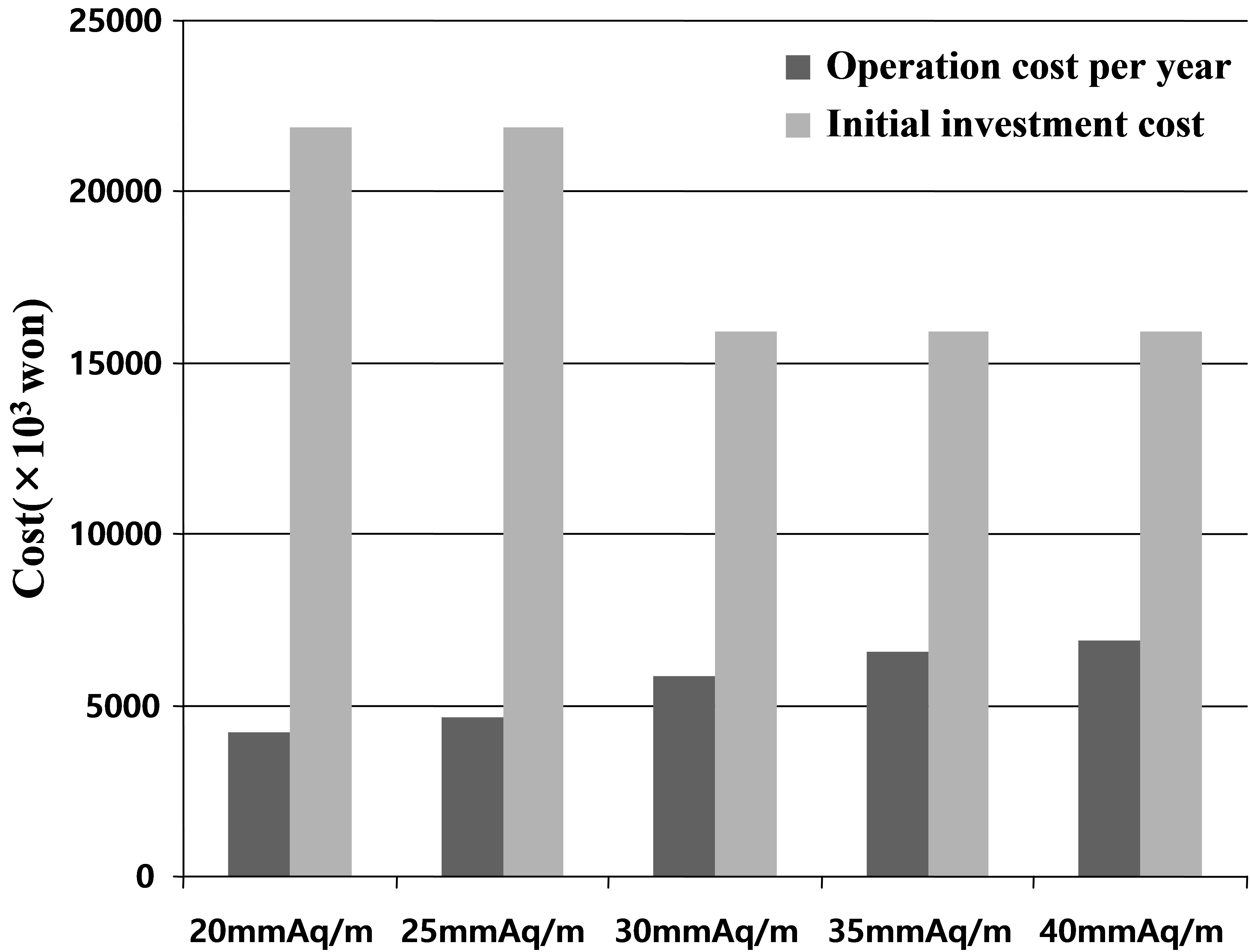
Fig. 4은 20, 25, 30 mmAq/m에 대해서 사용기간을 10년으로 가정하고 사용 년수에 따른 초기투자 비용과 펌프 구동비용을 합친 총 비용을 그래프로 나타낸 것이다. 35, 40 mmAq/m은 30 mmAq/m과 초기 비용은 같으면서 펌프 구동비용만 더 소모되기 때문에 그래프 상으로 교점이 존재하지 않는다.

Fig. 4 Comparison of the total costs over time.

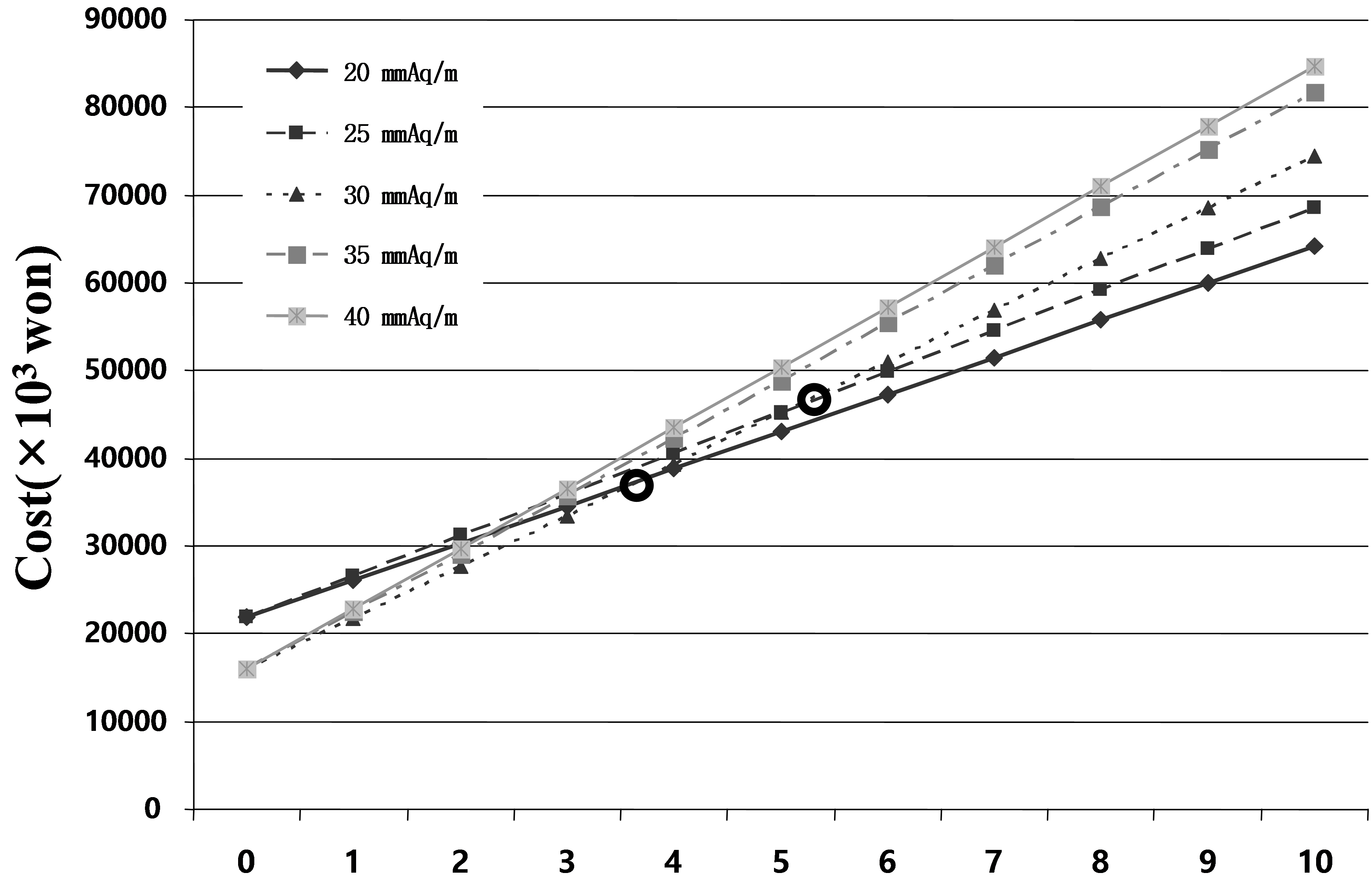
초기에는 30 mmAq/m인 경우가 비용이 적게 드나 약 4년 후에는 Fig. 4의 A와 같이 25 mmAq/m가 더 경제적인 것을 알 수 있다. 또한 설치비용이 낮은 200 A를 사용한 경우(30, 35, 40 mmAq/m)가 초기에는 경제적이지만, 어느 정도 시간이 지나면 펌프구동 비용이 점점 누적됨으로써 총 비용이 역전되어 250 A를 사용(20, 25 mmAq/m)한 경우가 더 경제적이게 된다.

단위마찰저항 값을 20 mmAq/m로 선정하여 배관을 설계하면 기존 단위마찰저항 값인 30 mmAq/m로 설계하였을 때 보다 약 1,024만 원 절약효과를 기대 할 수 있으며, 이는 10년 동안 사용할 시 소모되는 총 비용 대비 약 16%에 해당하는 값이다.

본 연구에서 제시한 방법으로 앞으로 배관 설계를 한다면 현 시점에서의 에너지 비용(자원비용에 따른 펌프가동비, 유지비 등)을 고려한 효과적인 설계가 이루어질 수 있다. 용도별 배관의 종류와 이에 필요한 양정량에 따라 어느 정도의 에너지가 필요하며, 변화하는 에너지 비용에 따라 어떤 경향을 보이게 되는지 위와 같이 그래프와 표를 통해 결과를 제시하여 설계 시 쉽게 고려할 수 있다. 이를 통해 향후 건물 배관시공이나 보수 시, 그 해당 시점에서의 에너지 비용을 적용하고, 이후의 에너지 비용변화의 경향을 파악하여 손쉽고 효과적이며 경제적인 설계가 가능해진다.

본 연구에서는 작동유체를 냉각수로 제한하여 연구 진행해 보았지만 실제 배관에는 다양한 용도가 있고, 이에 맞는 다양한 작동유체가 사용된다. 이렇게 다양한 배관과 작동유체에 대해서도 추가적인 변수를 고려한다면 동일한 방법으로 경제적인 배관단위마찰저항 값을 적용시켜 건물사용 수명에 대한 경제적인 비용을 선정할 수 있다.

4. 결 론

본 연구에서는 냉각수 사용조건하에 배관선정과 펌프선정 과정을 거쳐 배관설계 시 기존에 사용되는 단위마찰저항 값인 30 mmAq/m보다 경제적인 마찰저항 값을 찾고자 건물 내에서 사용되는 냉각수 배관에 대한 단위마찰저항 값을 변경시켜가며 배관경과 펌프의 축동력을 계산하였다. 그리고 현재의 전기요금 기준으로 축동력을 운전비용으로 환산하였다. 그에 따라 배관의 초기 설치비와 펌프 운전비용간의 관계를 파악하여 경제성분석을 하였다. 본 연구를 통하여 얻은 결과는 다음과 같다.

(1) 배관의 초기 비용이 급격히 변하는 단위마찰저항 20, 30 mmAq/m 구간에서 그래프 상의 교점은 약 4년으로 확인 할 수 있으며 사용 기간을 4년 이하로 사용하는 경우 단위마찰저항 30 mmAq/m값이 20 mmAq/m일 때 보다 경제적이다. 반대로 사용기간을 4년 이상으로 사용하는 경우 20 mmAq/m 값이 30 mmAq/m보다 더욱 경제적인 것을 알 수 있다.

(2) 배관을 오랫동안 사용할 경우, 단위마찰저항 값이 작으면 경제적으로 유리하며 반대의 경우 단위마찰저항 값이 클수록 더욱 경제적인 것을 알 수 있다. 그러므로 배관설계 시 배관의 사용기간을 정확히 판단하여 가장 경제적인 배관단위마찰저항 값을 선정하는 것이 중요하다.