Gonghee Lee
(이공희)
1,2†
Andong Shin
(신안동)
1
Aeju Cheong
(정애주)
1
-
Nuclear Safety Research Department, Korea Institute of Nuclear Safety, Daejon, 34142,
Korea
(한국원자력안전기술원 원자력안전연구실)
-
Nuclear and Radiation Safety Department, University of Science and Technology, Daejon,
34113, Korea
(과학기술연합대학원대학교 원자력 및 방사선 안전전공)
Copyright © 2016, Society of Air-Conditioning and Refrigeration Engineers of Korea
keywords
Computational fluid dynamics, Mixing vane, Rod bundle, Subchannel, Swirl-type, Turbulent flow
키워드
전산유체역학, 헌합날개, 봉다발, 부수로, 선회 형태, 난류 유동
기호설명
Dh:수력직경 [mm]
Fmixing:혼합인자
Fswirl:선회인자
H:나선도, 맴돌기 [m/s2]
l:연료봉간 대각선 길이 [mm]
P:연료봉간 피치 [mm]
s:연료봉 간극 [mm]
U,V,W:시간 평균 수평, 수직, 축방향 속도 [m/s]
Vdiag:대각선 길이 l에 수직한 속도 [m/s]
Vgap:연료봉 간극에서 교차유동 속도 [m/s]
Wbulk:체적속도 [m/s]
1. 서론
가압경수로에서 연료봉다발 표면의 적절한 열제거는 노심 열적여유도 확보를 통한 원자력발전소의 안전 운전에 매우 중요하다.
일반적으로 연료집합체에서 연료봉다발을 지지하는 지지격자(spacer grid)에는 혼합날개(mixing vane)가 설치된다. 상기 혼합날개는 난류
강화 기구로서 부수로(subchannel) 내부에서 선회류(swirl flow) 또는 연료봉 간극사이에서 횡류(cross flow)를 발생시켜 대류열전달을
증진시키는 역할을 한다(Fig. 1 참조). 따라서 혼합날개의 기하학적인 형상 및 배열 형태는 혼합날개의 성능을 결정하는 중요한 인자이다. 따라서 혼합날개의 기하학적인 형상 및 배열
형태는 혼합날개의 성능을 결정하는 중요한 인자이다.
Fig. 1. Flow patterns inside fuel assembly.
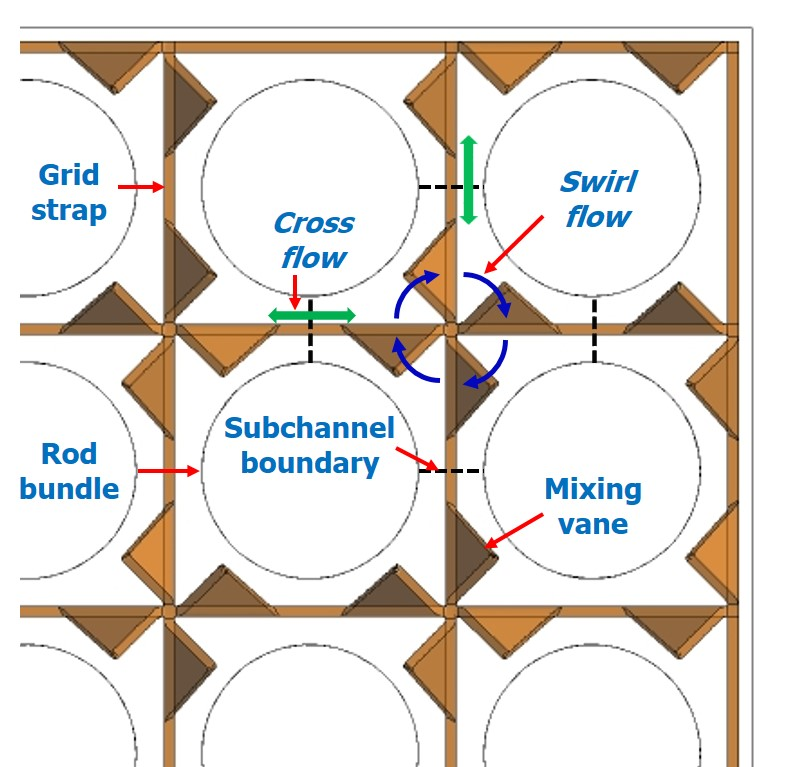
한편 지지격자 및 이에 부착된 혼합날개는 부수로 내부에서 상당한 유동혼합 및 국부적인 난류 강도를 증가시킬 수 있기 때문에 부수로 내부 유동의 예측은
등온(isothermal) 또는 단상(single phase) 조건에서 조차 매우 어려운 실정이다.
현재 원자력발전소 인허가 신청시 노심열수력 설계분야에서는 연료집합체 내부의 유동 및 엔탈피 분포를 예측하기 위해 COBRA 또는 VIPRE와 같은
부수로해석 전용 전산코드를 사용하고 있다. 그러나 이러한 부수로해석 코드는 기하학적인 형상에 종속된 혼합 인자(mixing factor) 및 지배방정식을
종결하기 위한 실험 상관식(empirical correlation)들에 의존한다. 한편 부수로 내부유동 예측시 전산유체역학(computational
fluid dynamics) 소프트웨어의 장점은 이러한 실험 상관식들에 부수로해석 코드와 동일한 수준으로 의존하지 않아도 된다는 점이다. 따라서 전산유체역학
소프트웨어로 계산된 결과들은 지지격자 하류의 주요 난류 구조 특성들을 파악할 수 있는 보다 광범위한 적용성을 가진다.
한편 많은 전산유체역학 소프트웨어들이 혼합날개가 장착된 연료집합체에서 복잡한 유동을 예측하기 위해 사용되어 왔으나, 상용 지지격자의 지적재산권 특성으로
인해 검증 계산용 시험자료의 활용은 매우 제한적이었다. 또한 현재 국내의 경우 원자력 규제기관으로부터 인허가를 받은 전산유체역학 소프트웨어는 없으며,
전산유체역학 소프트웨어의 종합적인 평가를 위한 지침도 마련되어 있지 않다. 따라서 규제 관점에서 국내 원자력안전 분야에 대한 전산유체역학 소프트웨어의
적용성에 관한 체계적인 평가 및 지침 마련이 필요하다. 이와 관련하여 한국원자력안전기술원에서는 대표적인 원자력 안전 문제인 원자로 및 연료집합체 내부유동
해석시 전산유체역학 소프트웨어의 예측 성능을 평가하는 연구를 수행하고 있다.((1)~(3))
본 연구에서는 OECD/NEA에서 벤치마크 계산((4),(5))으로 활용된 선회 형태(swirl-type)의 혼합날개가 장착된 5×5 연료집합체 내부의 유동분포 특성을 파악하기 위해 상용 전산유체역학 소프트웨어인
ANSYS CFX R.14(6)를 사용하여 계산을 수행하였고, 계산결과를 측정값과 비교하였다. 또한 선회 형태의 혼합날개 형상이 연료집합체 내부유동 형태에 미치는 영향에 대해
설명하였다.
2. 해석모델
2.1 시험장치
대기 압력 및 온도 조건에서 연료집합체에 대한 수력 시험을 수행하기 위해 한국원자력연구원에 설치된 MATiS-H 시험장치의 개략도를 Fig. 2에 나타내었다. 시험장치는 크게 물 저장탱크, 순환펌프 및 시험부로 구성된다.
Fig. 2. Schematic diagram of the MATiS-H test facility.(4)
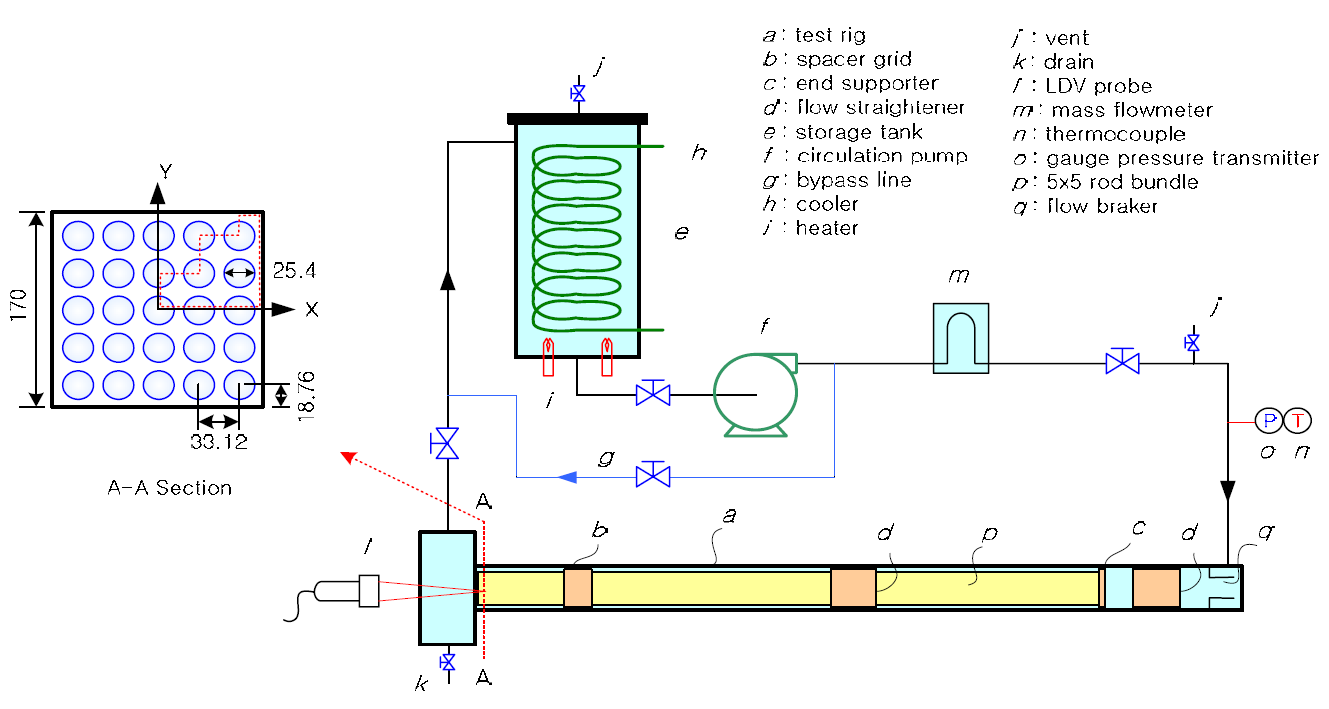
시험루프의 냉각재 온도는 물 저장탱크에 설치되어 있는 가열기 및 냉각기를 제어함으로써 ±1℃ 범위내에서 유지된다.(4) 냉각재 유량은 순환펌프의 회전속도를 변경함으로써 자동으로 조정된다.(4) 시험루프 변수들(유량, 압력 및 온도)을 감시하고 조정하기 위해 유량계, 게이지 압력 수송기 및 열전대가 시험부의 입구에 설치되었다. 모든 내부
장치들(연료봉 25다발, 지지격자, 혼합날개 및 지지물)은 스테인리스강으로 제작되었다.
수평 시험부의 주요 몸체는 3,863 mm 길이의 5×5 연료봉 다발을 포함해서 170×170 mm의 단면적에 4,670 mm 길이의 정방형 덕트로
구성된다. 유동 단면의 수력직경(Dh)은 24.27 mm, 연료봉간 피치(P)는 33.12 mm, 연료봉과 벽 사이의 피치는 18.76 mm이다. 시험에 사용된 연료봉의 외경은 부수로에서
횡방향 유동구조를 자세하게 파악하고 LDA(Laser Doppler Anemometry)의 측정 해상도를 향상시키기 위해 실제 연료봉에 비해 2.67배가
증가된 25.4 mm이다.
Fig. 3은 혼합날개가 선회 형태로 부착된 지지격자를 나타낸다. 선회 형태의 경우, 격자판(grid strap)의 교차지점에 4개의 혼합날개가 배치되고 개별
혼합날개는 대각선 기준으로 35°정도 굽어 있다.
Fig. 3. Spacer grid with the swirl-type mixing vanes.

Fig. 4와 같이 LDA 속도 측정은 지지격자의 혼합날개 끝부분으로부터 하류방향으로 Z = 0.5, 1.0, 4.0, 10.0 Dh 위치의 1/4 단면에서 측정되었다. 이 경우에 개별 Z 위치에서 수평 및 수직방향 속도성분 U, V는 부수로 1~3, 5~6, 9를 포함하는 영역에서
측정된 반면, 축방향 속도 성분 W는 연료봉간 중간 위치인 Y = 0.5, 1.5, 2.455 P에서 측정되었다. 체적(bulk) 속도로 무차원화된
속도 성분들에 대해 LDA 측정 불확실도는 95% 신뢰도에서 4.8~5.1%로 평가되었다.(4)
Fig. 4. LDA measurement region(4)(A-A section inFig. 2).

2.2 시험조건
시험에서는 35℃, 156.9 kPa 조건의 물이 작동유체로 사용되었다. 질량 유량은 24.2 kg/s, 체적 속도는 1.5 m/s이다. 따라서
체적 속도와 수력직경에 근거한 레이놀즈수는 50,250이다. 시험 조건의 평균값 및 이들의 불확실도를 table 1 에 요약하였다.
Table 1. Test conditions(4)
|
Parameters
|
Unit
|
Mean value
|
Uncertainty(%)
|
|
Mass flow rate
|
kg/s
|
24.2
|
0.29
|
|
Temperature
|
℃
|
35
|
2.90
|
|
Pressure
|
kPa
|
156.9
|
0.39
|
|
Bulk velocity
|
m/s
|
1.5
|
0.37
|
|
Reynolds number
|
|
50,250
|
2.01
|
3. 수치모델링
3.1 수치해법
본 연구에서는 상용 유동해석 소프트웨어인 ANSYS CFX R.14(6)를 이용하여 비압축성, 등온, 비정상 상태 조건하에서 5×5 연료집합체 내부의 난류 유동장을 계산하였다.
공간 차분 오차는 차분법의 정확도 및 격자 크기에 기인한다. 일반적으로 고차 정확도의 공간 차분법이 고품질의 계산결과를 제공할 수 있는 것으로 알려져
있다. 또한 유동이 격자선과 나란하지 않거나 복잡한 유동에 대해서는 1차 정확도의 차분법을 가급적 사용하지 않도록 권고하고 있다.(7) 따라서 본 연구에서는 운동량 방정식 및 난류 방정식의 대류항에 대해 2차 정확도에 준하는 고해상도(high resolution) 차분법을 적용하였다.
참고로 고해상도 차분법에서는 계산영역 전체에 대해 국부 해석결과를 이용하여 조합인자(blend factor) 크기를 결정한다. 변수의 구배가 작은
경우, 혼합 인자는 1에 근접한 값을 가지며 2차 정확도를 나타내는 반면 변수의 구배가 급격하게 변하는 경우, 해석 결과의 왜곡을 방지하고 강건성(robustness)을
유지하기 위해 혼합인자는 0에 근접한 값을 가지며 1차 정확도를 나타낸다. 저자(3)의 선행연구 결과에 따르면 고차 정확도의 차분법이 연료집합체 내부의 평균 속도장을 상대적으로 정확하게 예측하였다.
시간에 대한 차분법으로는 ANSYS CFX R.14(6)에서 기본적으로 제공하는 2차 정확도의 내재적인 시간 단계법인 Second Order Backward Euler 방법을 사용하였다.
비정상상태 계산을 위해 시간간격을 0.001 sec로 해서 유동발달 시간 3 sec까지 계산을 수행하였다. 매 시간단계별로 개별 방정식들의 제곱평균(root
mean square) 잔차가 10-5 이하인 경우에 수렴된 것으로 판정하였다.
3.2 난류모델
연료집합체 내부의 난류 유동을 계산하기 위해 SSG (Speziale, Sarkar and Gatski) 레이놀즈 응력모델을 사용하였다. 상기 난류모델은
개별 레이놀즈 응력에 대한 수송방정식을 계산함으로써 유선 곡률, 이차 유동, 변형률의 급격한 변화 등의 영향을 2방정식 난류모델에 비해 상대적으로
잘 고려할 수 있다. 상기 난류모델에 대한 상세한 설명은 ANSYS CFX 매뉴얼(8)에서 확인할 수 있다.
3.3 격자계
Fig. 5는 시험에 사용된 연료집합체와 동일한 크기의 계산 영역에 대해 ICEM-CFD 소프트웨어를 활용하여 생성한 격자계를 나타낸다.
Fig. 5. Grid system.

연료집합체 형상의 과도한 단순화를 방지하고 보다 효율적인 격자 분포를 위해 사면체, 웨지, 피라미드 및 육면체 형태로 구성된 혼합격자를 생성하였다.
벽 근처에서 격자 해상도를 향상시키기 위해 프리즘 형태의 격자를 배치하였다.
본 연구에서는 2가지 형태의 격자계에 대해 격자 민감도 평가를 수행하였다. 계산에 사용된 격자계에 대한 상세 정보를 table 2에 요약하였다.
Table 2. Grid information
|
Items
|
type A
|
type B
|
|
Total elements
|
1.61×107 |
3.51×107 |
|
Max. y+
|
27.3
|
10.3
|
|
Max. face angle
|
176.0°
|
173.8°
|
참고로 type B는 저자들의 가용 컴퓨터 용량에서 적용 가능한 최대 격자수이다.
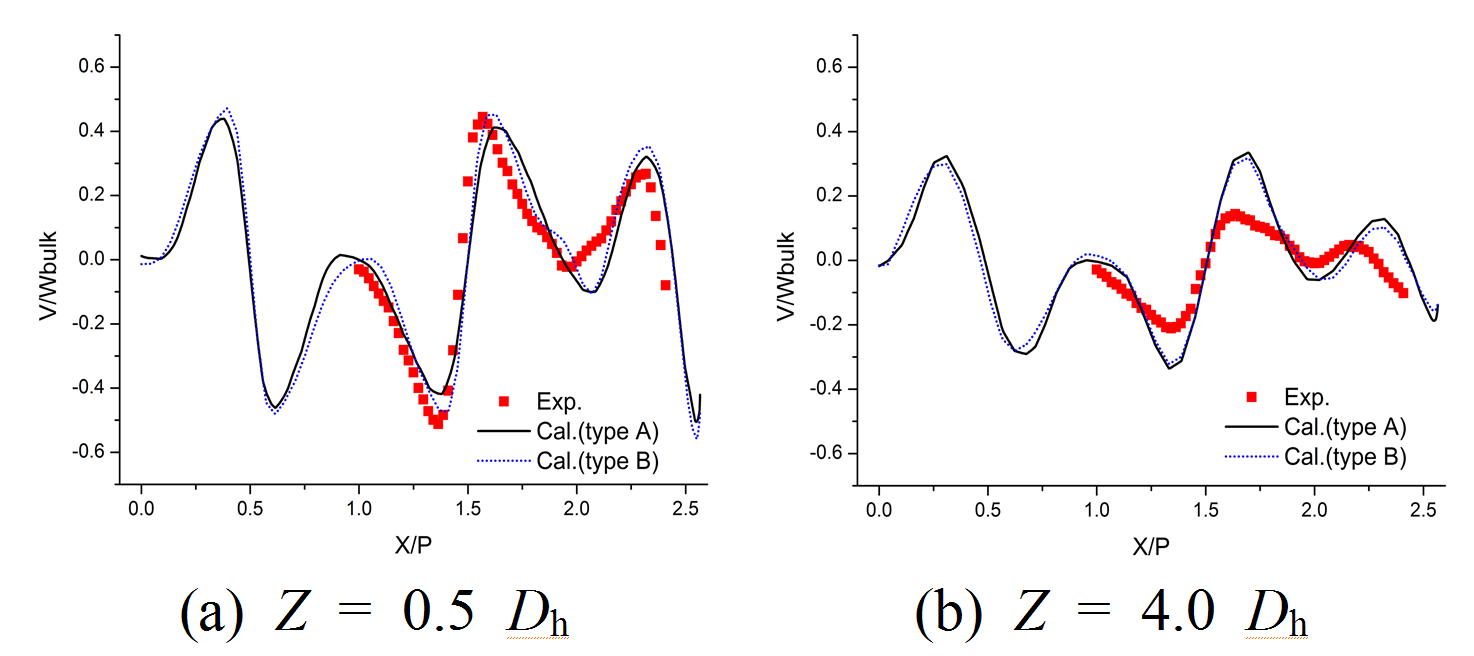
Fig. 6은 Y = 1.5 P에서 2가지 형태의 격자계로 계산된 시간 평균 수직방향 속도성분(V/Wbulk) 형상을 나타낸다. 전반적으로 속도 크기의 차이가 미미하였고, 과도한 비정상 계산 시간을 저감하기 위해 본 논문에서는 성긴 격자(1.61×107개, type A)에 대한 계산 결과를 설명하였다.
Fig. 6. Grid sensitivity results:time averaged vertical velocity(V/Wbulk) profile at Y = 1.5 P.
3.4 경계조건
계산시 입구조건으로 활용하기 위해 지지격자가 설치되지 않은 연료봉 다발에 대해 속도 성분이 추가적으로 측정되었으나, 측정부위가 입구 단면 전체가
아닌 일부분이어서 실제 계산에 적용하기에는 제한이 있었다. 따라서 본 연구에서는 유동방향으로 주기조건을 부여해서 완전 발달된 유동장을 별도의 계산을
통해서 얻었으며 이를 입구경계조건으로 활용하였다. 작동 유체로는 35℃의 물을 적용하였다. 출구경계면에서는 평균 정압(static pressure)
조건을 적용하였다. 연료봉, 혼합날개 등을 포함한 모든 벽 경계면에서는 점착(no-slip) 조건을 적용하였다. 벽 근처의 유동을 계산하기 위해 가변(scalable)
벽함수를 사용하였다.
4. 결과
Fig. 4(c)와 같이 지지격자의 혼합날개 끝단으로부터 하류방향으로 Z = 0.5, 1.0, 4.0, 10.0 Dh 위치에서 ANSYS CFX R.14로 계산한
결과와 측정값을 비교하였다.
4.1 시간 평균 속도장
4.1.1 속도벡터
Fig. 7(a)에서 볼 수 있듯이 혼합날개 끝단으로부터 하류방향으로 Z = 1.0 Dh에서는 주로 선회류에 의해 원형에 가까운 와류가 부수로 1, 2, 4, 5번 내부에서 형성되었다. 연료봉 간극사이를 통과하는 횡류의 크기는 상대적으로
작았다.
Fig. 7. Time averaged velocity(U, V) vector for the swirl-type mixing vanes(left:experiment, right:calculation).

예측된 속도벡터는 혼합날개의 배치 방향에 따라 시험 결과와 동일하게 부수로 1, 5번에서는 반시계 방향 와류를, 부수로 2번에서는 시계방향 와류를
나타내었다. 한편 혼합날개가 격자판에 불완전한 형태로 부착되어 있고 정방형 덕트 벽으로 인해 최외곽 연료봉들 사이에 위치한 부수로 3, 6~9번 내부에서는
와류의 형태가 원형에서 다소 일그러졌고 와류의 크기도 상대적으로 축소되었다.
혼합날개 끝단으로부터 하류방향으로 Z = 10.0 Dh에서는 유동이 하류로 진행하면서 선회류의 크기가 감쇠하였으나, 부수로 1, 2, 4, 5번
내부에서 와류 형태는 원형을 유지하였다(Fig. 7(b) 참조).
전반적으로 계산된 와류 형태 및 와류 중심 위치는 시험 결과와 비교적 잘 일치하였다.
4.1.2 수평방향 속도성분(U/Wbulk)
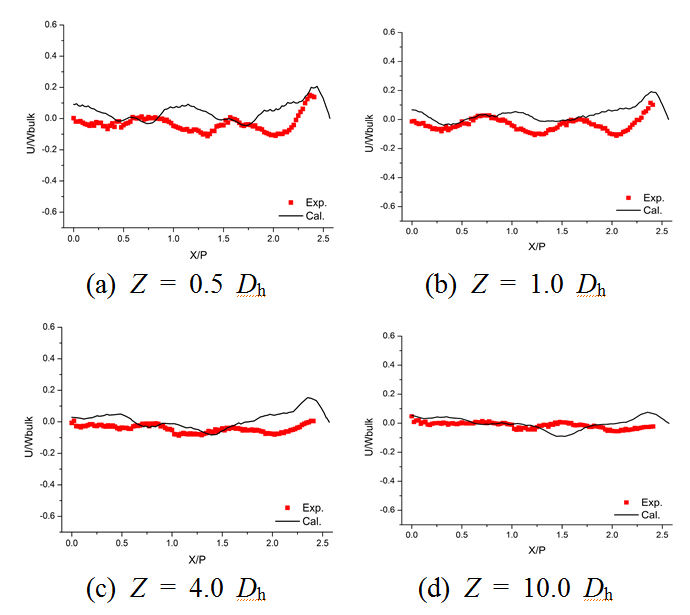
Fig. 8은 Y = 0.5P(해당 위치는 Fig. 4 참조)에서 시간 평균 수평방향 속도성분 형상을 나타낸다. 균형 배치된 혼합날개에 의해 수평방향의 인접 부수로로 이동하는 횡류가 거의 발생하지 않고
선회류가 우세하므로 혼합날개를 통과한 유동의 수평방향 속도성분은 다른 속도성분들(V, W)에 비해 크기가 작으며 유동이 하류로 진행할수록 음(-)과
양(+)의 속도 첨두값이 점차 감소하면서 편평한 형태를 나타내었다.
Fig. 8. Time averaged horizontal velocity(U/Wbulk) profile at Y = 0.5 P.
4.1.3 수직방향 속도성분(V/Wbulk)
Fig. 9는 Y = 0.5 P에서 시간 평균 수직방향 속도성분 형상을 나타낸다. 부수로 내부의 선회류에 의해 와류 중심(X/P≈0.5, 1.5)을 기준으로
음(-)과 양(+)의 첨두값이 발생하는 파형의 속도 형상이 나타났다가 유동이 하류로 진행할수록 속도 첨두값이 점차 감소하였다. 또한 2개의 부수로가
접하는 경계면(X/P = 1.0)을 기준으로 속도 형상이 거의 대칭 형태를 나타내었다. 이는 Fig. 7에서 볼 수 있듯이 선회 형태 혼합날개의 경우 부수로 내부에서의 와류 형태가 거의 원형을 나타냈기 때문인 것으로 판단된다.
Fig. 9. Time averaged vertical velocity(V/Wbulk) profile at Y = 0.5 P.
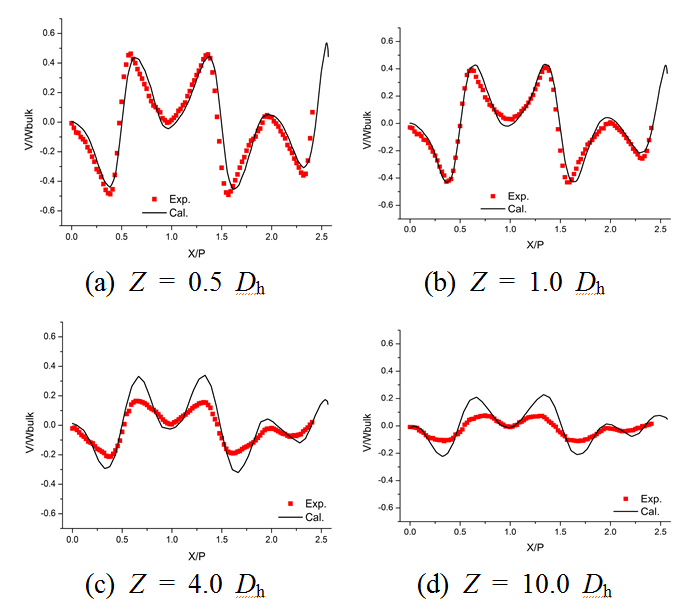
Z = 4.0 Dh 및 10.0 Dh에서 계산 결과가 시험 결과에 비해 음(-)과 양(+)의 속도 첨두값을 다소 크게 예측한 것을 제외하고 계산된
속도형상은 시험 결과와 전반적으로 일치하였다. 이러한 차이가 발생한 원인은 수치확산(numerical diffusion) 오차에 의해 비롯된 것이라기
보다는 ANSYS CFX가 혼합 날개를 통과한 유동의 혼합 정도를 시험 결과와 차이나게 예측했기 때문인 것으로 판단된다.
4.1.4 축방향 속도성분(W/Wbulk)
Fig. 10은 Y = 0.5 P에서 시간 평균 축방향 속도성분 형상을 나타낸다. 유동이 하류로 진행할수록 혼합날개로 인해 발생한 W/Wbulk의 부족(defect) 현상이 사라지면서 시간 평균 축방향 속도성분은 점차 편평한 형태를 나타내었다. 예측된 W/Wbulk은 혼합날개 끝단 부근(Z = 0.5 Dh, 1.0 Dh)에서는 시험 결과와 전반적으로 일치한 반면 유동이 하류로 진행(Z = 4.0 Dh, 10.0 Dh)하면서 음(-)과 양(+)의 첨두값이 상대적으로 크게 나타났으며 속도 형상도 더욱 빈번하게 변화하였다.
Fig. 10. Time averaged axial velocity(W/Wbulk) profile at Y = 0.5 P.
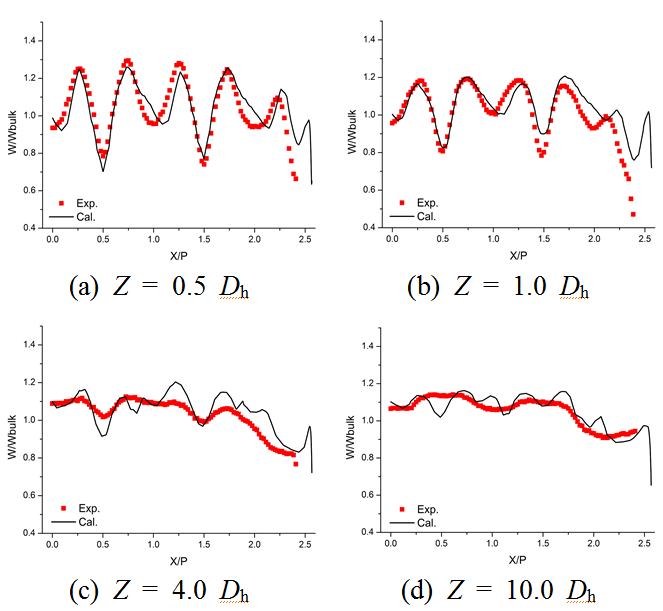
이상과 같이 본 연구에서 ANSYS CFX R.14(6)로 계산한 평균 속도장 결과의 신뢰성을 평가하기 위해 식(1)을 사용해서 시험결과와 비교하였다.
여기서 N은 Y = 0.5 P에서 시험 자료수를, velcomp,i와 velEXD,i는 해당 동일 위치에서의 계산 및 측정된 속도성분(U, V, W)을 나타낸다.
비교 위치로 Y = 0.5 P를 선택한 이유는 해당 위치가 벽 근처의 영향이 적고 전형적인 부수로 유동형태를 나타내기 때문이다.
table 3 은 축방향 해당 위치에서 식(1)로 계산된 점수표를 나타낸다. 총 점수는 74.083으로 평가되었으며, OECD/NEA 벤치마크 계산 참여자들의 평가 결과인 46.03~165.12범위에
포함되었다. 따라서 본 연구에서 사용된 수치모델링은 타당하며, 계산된 평균 속도장 결과는 신뢰할 수 있을 것으로 판단된다.
Table 3. Scores of time averaged velocity components along the measurement locations
|
|
Location
|
Z = 0.5Dh |
Z = 1.0Dh |
Z = 4.0Dh |
Z = 10.0Dh |
Total
|
|
Velocity
|
|
|
U/Wbulk |
1.61×107
|
1.61×107
|
3.51×107
|
3.51×107
|
3.51×107
|
|
V/Wbulk |
7.266
|
4.517
|
7.123
|
6.059
|
24.964
|
|
W/Wbulk |
6.747
|
6.509
|
5.617
|
4.044
|
22.918
|
|
Total
|
22.498
|
18.292
|
19.049
|
14.244
|
74.083
|
4.2 축방향 평균 와도(Vorticity)
Fig. 11은 부수로 내부의 시간 평균 축방향 평균 와도(ωz) 분포를 나타낸다. 와도 분포는 부수로에서 측정된 수평 및 수직방향 속도 성분을 사용해서 식(2)와 같이 정의될 수 있다.
Fig. 11. Time averaged axial vorticity contour for the swirl-type mixing vanes(left:experiment, right:calculation).

혼합날개 끝단으로부터 하류방향으로 Z = 1.0 Dh에서 예측된 축방향 평균 와도는 부수로 1, 2, 4, 5번 내부에서 원형에 가까운 분포 형태를 나타내었다. 유동이 하류로 진행하면서 Z = 10.0
Dh에서는 혼합날개에 의한 선회류의 강도가 약해지면서 와도 크기는 점차 감쇠하였으나, 연료봉 간극사이를 통과하는 횡류의 크기가 작아서 와도 중심은
대체적으로 부수로 중앙에서 유지되었다.
4.3 와류 중심 영역과 유선
Fig. 12는 부수로 내부의 맴돌이(helicity) 절대값 분포 및 유선(streamline)을 나타낸다. 맴돌이 절대값은 ANSYS CFX에서 와류 중심
영역을 확인하는 방법 중의 하나이며, 식(3)과 같이 평균속도와 와도의 내적의 절대값으로 정의된다.
Fig. 12. Streamlines and the absolute helicity contour for the swirl-type mixing vanes.
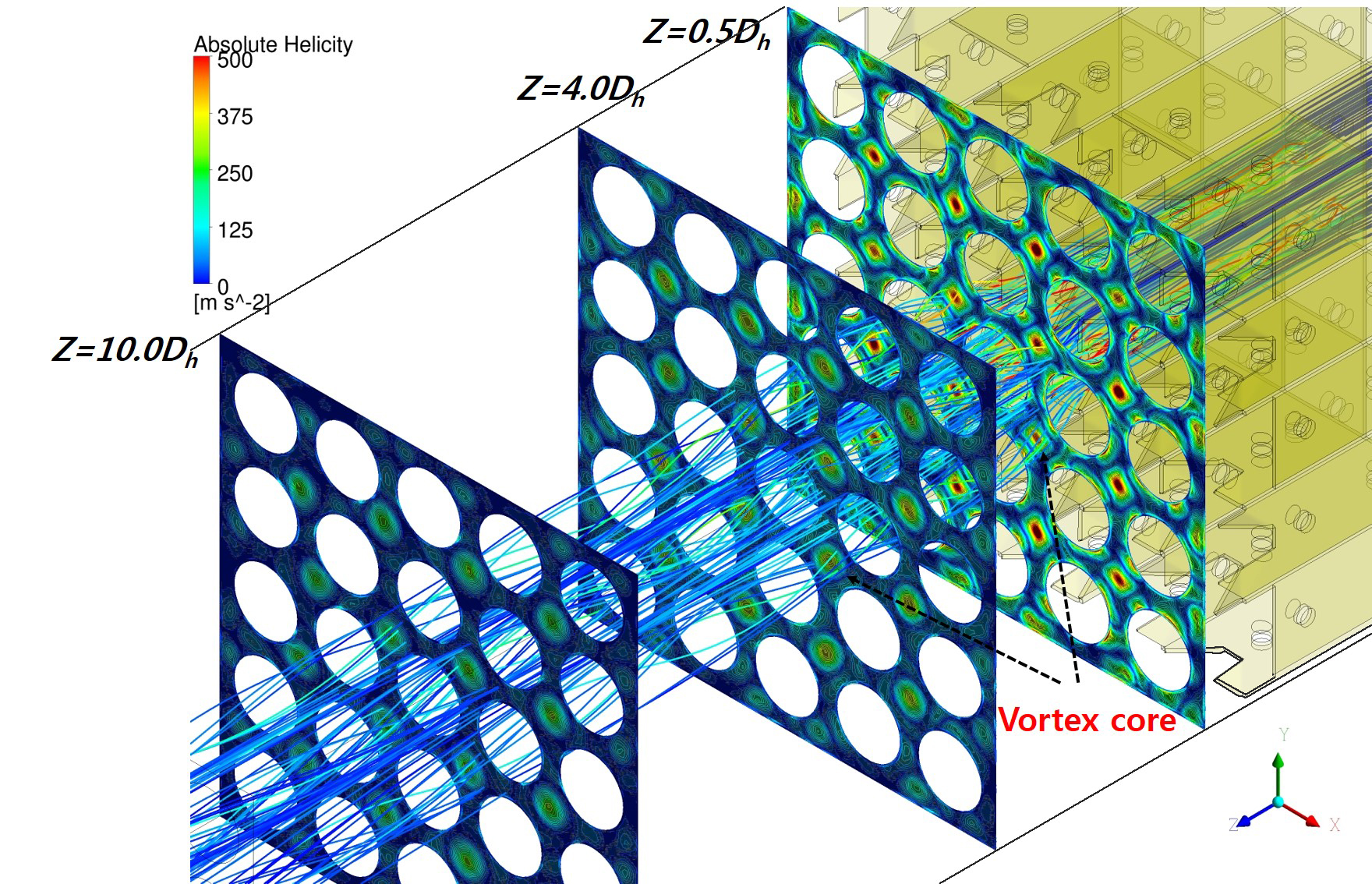
맴돌이 절대값의 첨두값이 분포하는 영역이 와류 중심을 나타내며, 상기 영역은 Fig. 11에서 축방향 와도의 음(-)과 양(+)의 첨두값이 분포하는 곳과 거의 일치한다. 또한 상기 영역을 통과하는 유선은 나선형태를 나타내었다.
4.4 선회인자(Swirl Factor)
부수로 중심에서 선회유동의 강도를 나타내는 선회인자는 식(4)와 같이 정의될 수 있다.
여기서 l은 연료봉간 대각선 길이를,
은 대각선 길이 l에 수직한 속도를 나타낸다. 따라서 선회인자는 부수로당 2개의 대각선에서 계산된 값을 평균한 것이다.
Fig. 13은 일부 부수로들(SC#1, 2, 5번; 여기서 SC#는 부수로 위치를 의미함)에 대해 혼합날개 끝단으로부터 하류 방향으로 선회인자의 크기 변화를
나타낸다 (부수로 위치는 Fig. 4(a) 참조). 유동이 하류로 진행할수록 시험 및 계산 결과에서 선회인자 크기는 감소하는 경향을 나타내었다.
Fig. 13. Swirl factor for the selected subchannels.

일반적으로 연료집합체에서 국부 임계열속은 혼합날개 끝단으로부터 하류 방향으로 거리가 증가함에 따라 지수함수 형태로 감소하는 경향이 있는 것으로 알려져
있다. 선회류는 대류열전달을 증진시키는 역할을 하므로 선회인자의 크기 감소는 국부 임계열속의 감소와 관련성이 있을 것으로 판단되며, 따라서 선회류의
크기 감소 경향은 Fig. 13과 유사할 것으로 예상된다.
다만 측정 및 계산된 국부 속도의 차이로 인해 혼합날개 끝단으로부터 하류 방향으로 Z = 4.0 Dh까지 구간에서 측정된 선회인자의 감쇠율이 계산값에 비해 크게 나타났다.
4.5 혼합인자(Mixing Factor)
연료봉 사이의 간극을 통과하는 교차유동의 크기는 지지격자에 부착된 혼합날개의 배치 형태에 의존하며, 교차유동의 강도를 나타내는 혼합인자는 식(5)와 같이 정의될 수 있다.
여기서
은 2개의 부수로가 접하는 면의 연료봉 간극에서 교차유동 속도를, s는 연료봉 간극을 나타낸다. 혼합인자는 부수로당 4개의 간극에서 계산된 값을 평균한
것이다.
Fig. 14는 선회 형태의 혼합날개가 균형 배치된 일부 부수로들(SC#1, 2, 5번)에 대해 혼합날개 끝단으로부터 하류 방향으로 혼합인자의 크기 변화를 나타낸다.
부수로 내부에서는 혼합날개에 의해 인접 부수로 이동하는 횡류가 거의 발생하지 않고 선회류가 우세하므로 혼합인자는 Fig. 13의 선회인자 대비 상대적으로 크기가 작다.
Fig. 14. Mixing factor for the selected subchannels.
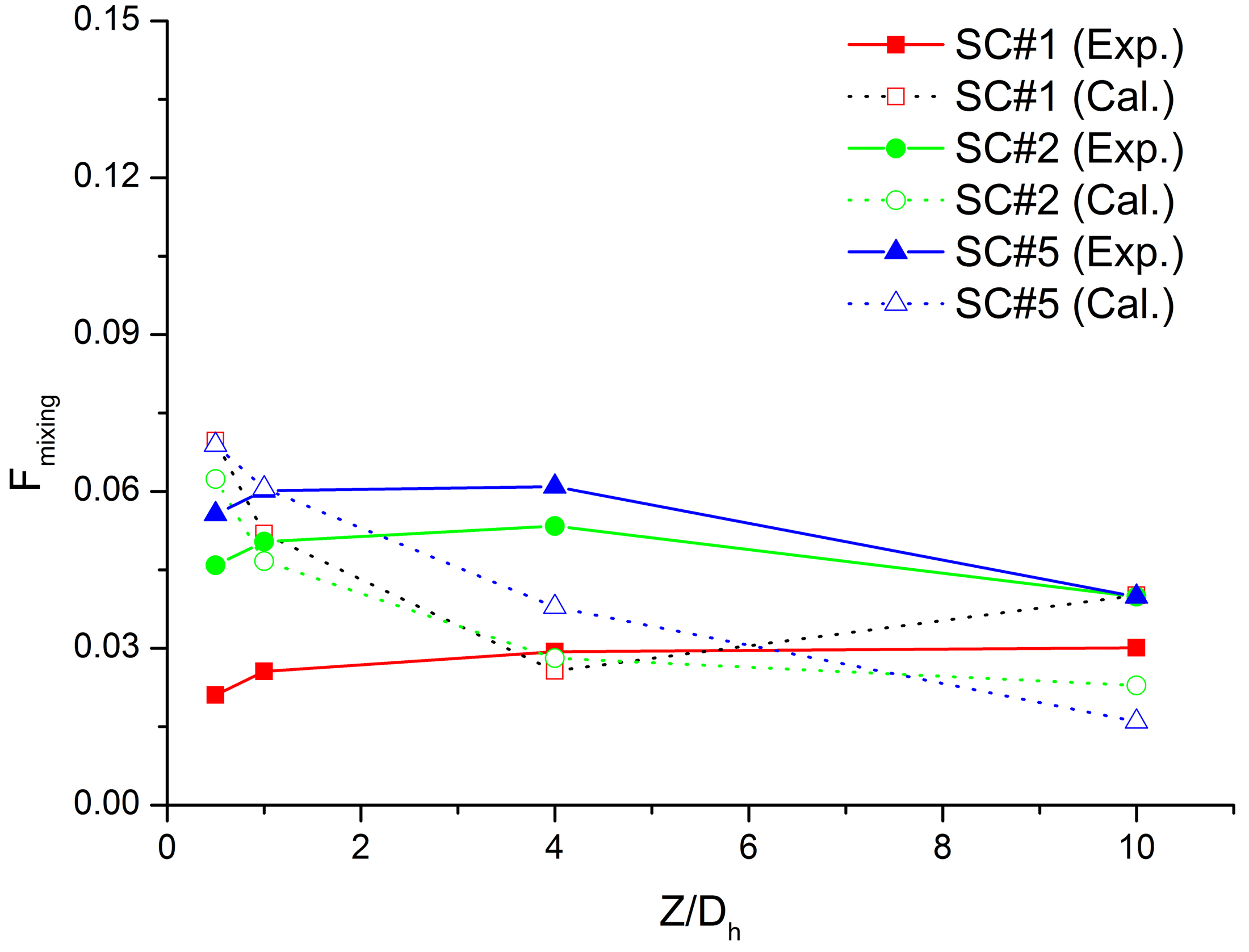
시험의 경우, 부수로 2, 5번(SC#2, 5)에서 측정된 혼합인자 크기는 Z = 4.0 Dh까지 유지 또는 약간 증가한 후 Z = 10.0 Dh에서 조금 감소한 반면 부수로 1번(SC#1)에서는 Z = 10.0 Dh까지 혼합인자 크기가 감소되지 않았다. 한편 계산의 경우, 부수로 2, 5번(SC#2, 5)에서 예측된 혼합인자 크기는 유동이 하류로 진행할수록 감소한
반면 부수로 1번(SC#1)에서는 Z = 4.0 Dh까지 감소한 후 Z = 10.0 Dh에서 약간 증가하였다. 혼합인자 측정값과 예측 결과 사이의 경미한 차이는 Fig. 8과 Fig. 9에서 볼 수 있듯이 측정 및 계산된 국부 속도의 차이에서 비롯된 것으로 판단된다.
5. 결 론
본 연구에서는 OECD/NEA에서 벤치마크 계산으로 활용된 선회 형태의 혼합날개가 장착된 5×5 연료집합체 내부의 유동분포 특성을 파악하기 위해
상용 전산유체역학 소프트웨어인 ANSYS CFX R.14를 사용하여 계산을 수행하였고, 계산결과를 측정값과 비교하였다. 또한 선회 형태의 혼합날개
형상이 연료집합체 내부유동 형태에 미치는 영향에 대해 살펴보았다. 주요 결론은 다음과 같다.
(1) ANSYS CFX R.14가 연료집합체 내부의 시간 평균 속도장을 일정 부분 타당한 수준으로 예측할 수 있음을 확인하였다. 다만 계산결과와
측정값 사이의 국부적인 차이로 인해 일부 변수들(예:혼합인자 등)은 서로 다른 경향성을 나타내었다.
(2) 균형 배치된 선회 형태의 혼합날개에 의해 수평방향의 인접 부수로로 이동하는 횡류가 거의 발생하지 않고 선회류가 우세하므로 혼합날개를 통과한
유동은 부수로 내부에서 원형에 가까운 와류 형태를 나타내었다. 또한 선회인자는 혼합인자 대비 상대적으로 큰 값을 나타내었다.
(3) 유동이 하류로 진행하면서 혼합날개에 의한 선회류의 강도가 약해지면서 와도 크기는 점차 감쇠하였으나, 연료봉 간극사이를 통과하는 횡류의 크기가
작아서 와도 중심은 대체적으로 부수로 중앙에서 유지되었다.
후 기
본 연구는 원자력안전위원회의 재원으로 한국원자력안전재단의 지원을 받아 수행한 원자력안전연구사업의 연구결과입니다(No. 1305002). 또한 한국과학기술정보연구원/슈퍼컴퓨팅센터로부터
슈퍼컴퓨팅 자원과 기술지원(과제번호:KSC-2015-C1-019)을 받아 수행된 연구성과입니다. 본 연구의 수행과 관련하여 실험 자료 및 기술적 조언을
해주신 한국원자력연구원 송철화 박사님, 장석규 박사님, 이재룡 박사님께 감사의 말씀을 드립니다.
References
Lee G. H., Bang Y. S., Cheong A. J., 2015, Comparative study for modeling reactor
internal geometry in CFD simulation of PWR and PHWR internal flow-Nuclear regulatory
perspective, Progress in Nuclear Energy, Vol. 85, pp. 588-599

Lee G. H., Cheong A. J., 2015, CFD analysis for the turbulent flow distribution in
a fuel assembly with the split-type mixing vanes by using the advanced scale-resolving
turbulence models, Applied Mechanics and Materials, Vol. 752/753, pp. 902-907

Lee G. H., Cheong A. J., 2015, Effect of the accuracy order of the discretization
scheme on the prediction performance for the turbulent flow structure inside fuel
assembly:Sensitivity study, Proc. of the ASME-JSME-KSME Joint Fluids Engineering Conference
2015, AJK2015-03027, Seoul, Korea.

Chang S. K., Kim S., Song C. H., 2014, Turbulent mixing in a rod bundle with vaned
spacer grids:OECD/NEA-KAERI CFD benchmark exercise test, Nuclear Engineering and Design,
Vol. 279, pp. 19-36

Lee J. R., Kim J. W., Song C. H., 2014, Synthesis of the turbulent mixing in a rod
bundle with vaned spacer grids based on the OECD-KAERI CFD benchmark exercise, Nuclear
Engineering and Design, Vol. 279, pp. 3-18

ANSYS CFX, Version 14.0, ANSYS Inc.

Menter F., 2001, CFD best practice guidelines for CFD code validation for reactor
safety applications, ECORA CONTRACT N° FIKS-CT-2001-00154.

2011, ANSYS CFX-Solver Modeling Guide, ANSYS Inc.
