1. 서론

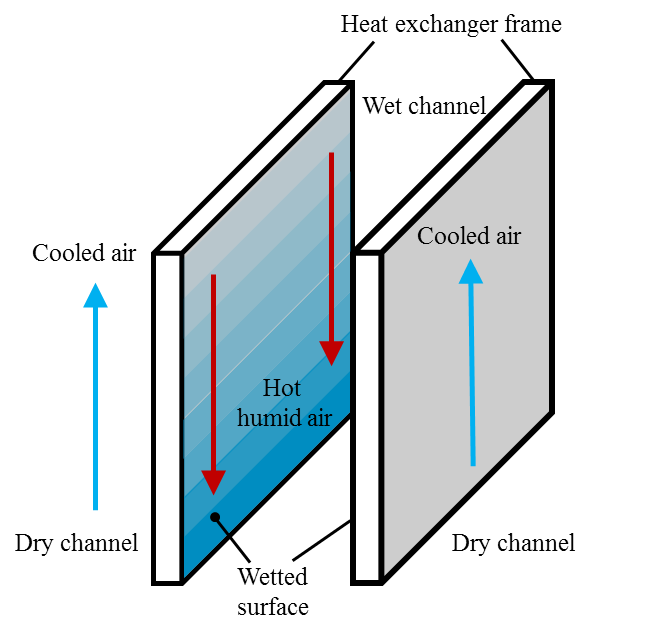
제습냉방 시스템은 여름철 습도가 높은 실내외 공기를 제습로터에 통과시켜 제습한 후, 증발식 열교환기를 통하여 냉각시켜 실내로 토출하는 시스템이다. 제습냉방 시스템의 핵심이 되는 증발식 열교환기는 제습로터를 통과한 건조 공기가 통과하는 건채널과, 별도로 분사된 물이 증발되면서 냉각된 습공기가 흐르는 습채널로 이루어져있다.(1) 증발식 열교환기의 성능에 가장 큰 영향을 미치는 요인으로 습채널 표면에 물이 고르게 퍼지게 하는 친수성 소재 및 형상 기술을 꼽을 수 있다. 습채널 표면의 친수성을 높이기 위하여 실리카액 등을 사용하는 친수 코팅 방법이 일반적으로 사용된다. 하지만 코팅막은 장시간 시스템 작동 시 표면 침식(erosion)과 벗겨지는 등의 문제가 발생할 수 있다. 친수 코팅의 벗겨짐 등으로 인한 습채널 표면의 젖음도(wettability) 저하는 제습냉방 시스템의 COP를 감소시키며 그 상관성은 매우 크다고 알려져 있다.(2) 열교환기 표면의 친수성을 증가시키는 방법으로 친수 코팅 외에, air-plasma를 이용하여 표면의 일시적인 초친수성으로 개질하거나,(3) chemical vapor deposition을 이용하여 초친수성 재료를 표면에 입히는 방법이(4) 있다. 하지만 위와 같은 방법으로 제조된 표면을 판-판(plate fin) 형태인 증발식 열교환기에 적용하는 것은 기술적으로 매우 어렵다. 또한 친수 처리된 표면의 친수성 지속 시간은 친수 코팅 처리된 표면과 비교하여 매우 짧은 것으로 알려져 있다. 증발식 열교환기 표면 젖음도의 내구성 및 장시간 사용 신뢰성을 높이는 방법으로 습채널의 표면을 다공성 멤브레인 형태로 제조하는 사례도 보고된 바 있다.(5) 친수성 다공성 멤브레인 구조는 친수 표면 처리 혹은 코팅에 비해 장기적인 사용이 가능하나, 제조 공정이 매우 복잡한 단점이 있다. 본 연구에서는 열교환기에 별도의 표면 처리를 하거나, 소재를 바꾸지 않으면서, 열교환기의 표면 구조 및 형상 제어를 통하여 Fig. 1과 같은 수직 대항류 구조의 증발식 열교환기 표면 친수성을 증가시키는 방안을 연구하였다. 표면 친수성 증가를 위하여 모세관 현상이 일어나는 작은 수직 층상구조(lamellar structure)가 열교환기 습채널 표면에 배열되어 있으며, 각 개방 채널 내부 표면 장력에 의한 물기둥 상승을 이론적으로 분석하였다. Lamellar 구조의 깊이 및 너비에 따라 물기둥의 표면 에너지 및 중력 포텐셜 에너지가 평형을 이루는 물기둥 높이(capillary length)를 이론적 모델링을 통하여 계산하였다. 이론적 모델링의 결과는 유한요소 해석 (FEM) 기반의 SE-FIT(surface evolver, version 1.12)(6) 프로그램의 결과와 비교하였으며, 그 차이에 대한 분석 및 고찰을 하였다.

Fig. 1. Schematic diagram of a hydrophilic heat exchanger walls for the evaporative cooling system.

2. 이론 및 해석 조건

평판 위에 올려진 물방울의 접촉각은 판 소재와 표면 조건 등에 의하여 결정이 된다. 깨끗한 유리 표면 위에 올려진 순수한 물방울은 초친수성을 나타내며 접촉각은 0°에 근접하게 된다. 하지만 유리 표면 혹은 물에 오염 물질이 포함될 경우 접촉각은 증가한다. 일반적으로 증발식 열교환기의 프레임 소재로 사용되는 알루미늄의 경우, 물방울의 접촉각은 세척 방법 등에 따라 60°에서 80°로 보고된 바 있다.(7) 본 연구에서 대상이 되는 열교환기 표면은 깨끗한 알루미늄 표면과 비슷한, 접촉각 60°을 가지는 약친수성 표면으로 가정하였다. 증발식 열교환기는 Fig. 1과 같이 수직으로 배열된 열교환기 표면에 물이 분사되는 형태이다. 분사된 물은 중력에 의하여 열교환기 표면에 머무르지 않고 낙하를 하게 된다. 열교환기의 표면 친수성이 강한 경우 혹은 접촉각 이력현상(hysteresis)이 높은 경우가 아니면 액적은 열교환기 표면에 젖어 있지 못하게 된다. 증발식 열교환기는 습채널 표면의 수막이 증발하면서 건채널을 통과하는 공기의 현열(sensible heat)을 뺏어오는 구조를 가진다. 습채널 표면에 얇고 균일하게 수막이 덮여있는 상태에서 열교환 성능이 극대화된다. 지나치게 두꺼운 물층에서는 얇은 경우 대비 증발을 위한 온도 상승이 제한되며, 젖지 않은 습채널 표면에서는 잠열 열전달 효과가 일어나지 않기 때문이다. 이와 같은 습채널 표면 및 얇은 수막 구조를 구현하기 위하여 습채널의 표면 친수성과 젖음에 대한 이해가 필요하다. 증발식 열교환기 윗면에서 습채널로 분무되는 물을 무시하는 경우, Fig. 2(a)와 같이 바닥에 물의 자유표면 (free surface)이 존재하는 경우를 고려한다. 이 경우에 아무리 열교환기 표면의 친수성이 높아, 물의 접촉각이 0°에 근접하더라도, 물의 접촉선 상승은 제한된다. 물의 자유표면에 맞닿은 평판과 물의 접촉각이 θE일 때, 최대로 올라가는 물높이(L)는 다음 식과 같이 알려져 있다(σ : 표면장력, ρ : 물의 밀도, g : 중력가속도).(8)

Fig. 2. Schematic diagrams of water imbibition for three different models. (a) Vertical smooth surface; (b) rectangular capillary tube; (c) open channel capillary tube.

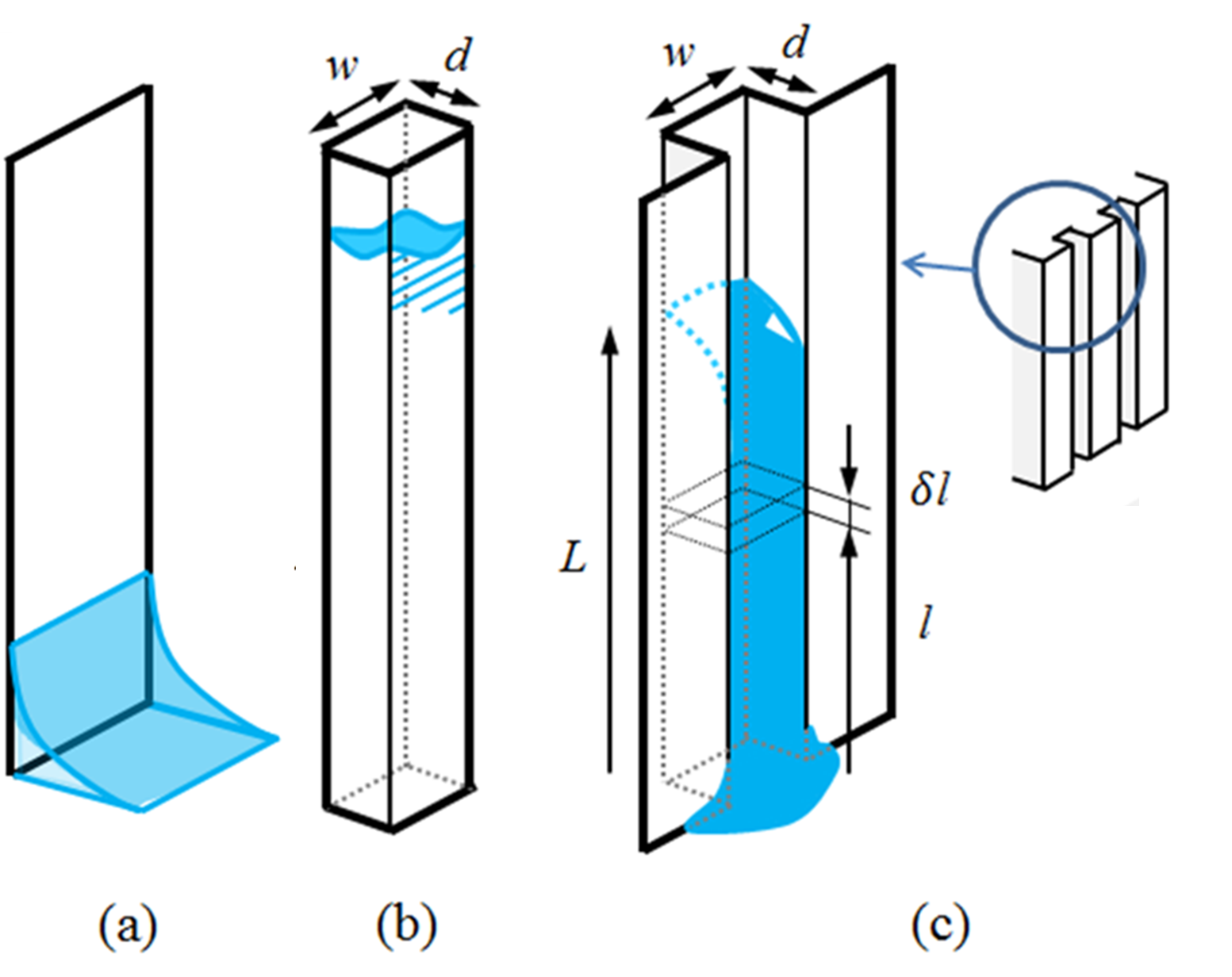
상온 상태 물의 경우, 접촉각이 0°인 표면에 닿아 있을 때 접촉선의 최대 높이는 2.73 mm에 불과하다. 이러한 접촉선의 높이를 가장 높이 올릴 수 있는 방법으로는 직경이 작은 모세관(capillary tube)과 같이 4면이 막힌 관을 만드는 방법이 있다(Fig. 2(b)). 하지만 이 경우, 습채널에 노출된 공기 면적이 제한되기 때문에 증발식 열교환기 구조로는 적절하지 않다. 따라서 모세관과 유사한 수준의 물높이를 가지면서 증발식 열교환 구조로 사용할 수 있는, Fig. 2(c)와 같이 개방 채널(open channel) 구조를 본 연구에서는 고려하였다. 개방 채널의 깊이(d)과 너비(w)를 변화시키면서 표면장력 때문에 상승한 물기둥의 높이를 계산하여, 간접적으로 습채널 표면의 젖음도를 예측할 수 있다. 위와 같은 구조에서 물기둥의 상승 높이를 예측하기 위하여 물기둥에 영향을 미치는 중력과 표면 에너지를 고려하였다. 물기둥의 높이는 Fig. 2(c)에 나타내어진 바와 같이, 미소 부피 상승 시(δl) 표면 에너지의 감소값(dEs)과 중력 포텐셜 에너지의 증가값(dEg)의 합이 0이 되는 지점의 높이를 찾으면 된다. 물기둥의 단면 형상은 사각형으로 가정하였다. 개방 채널의 폭과 깊이가 물기둥의 높이와 비교하여 매우 작을 경우, 물기둥 형상을 사각 기둥으로 가정할 수 있다. 이 때, 미소 높이(δl)의 상승으로 감소하는 표면 에너지(dEs)는 다음과 같다.

식(2)가 식(3)과 같아지는 점이 물기둥의 표면에너지와 중력에너지가 평형을 이루는 상태이며, 이때의 물기둥의 높이(L)는 아래와 같이 표현할 수 있다.

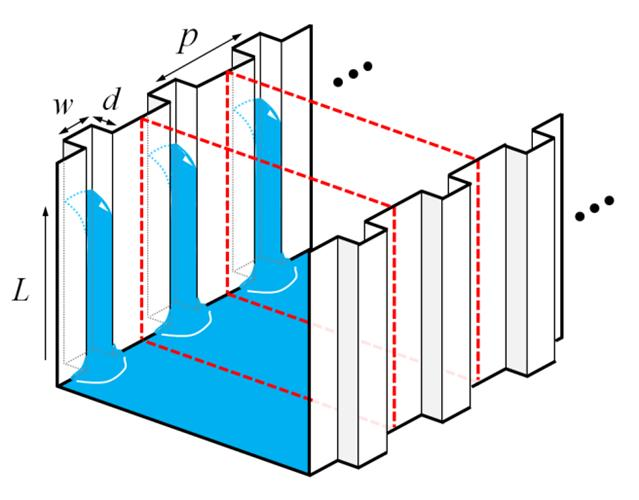
Fig. 3. Schematic diagram of lamellar patterned vertical heat exchanger for analysis.

위 식을 통하여 한쪽 면이 공기에 노출된 개방 채널에서의 물기둥 상승을 예측할 수 있다.

3. 해석 결과 및 분석

식(4)에서 도출한 개방 채널 구조의 물기둥 높이 이론식을 검증하기 위하여 액체 표면 해석 프로그램인 SE-FIT(Surface Evolver-Fluid Interface Tool, v1.12)을 사용하여 개방 채널 형상에 따른 물기둥의 높이를 계산하였다. 개방 채널의 3차원 모델링을 위하여 Fig. 3과 같이 증발식 열교환기의 습채널 구조를 고려하였다. 대칭 구조의 습채널 array 중에서 점선 부분 패턴을 해석 영역으로 설정하였다. 단일 채널 옆면은 대칭 경계 조건으로 가정하고 분석하였다. 벽면에서의 물 접촉각은 60°, 패턴이 반복되는 간격(p)은 5 mm, 마주보고 있는 열교환기 판 사이의 간격은 평판에 의해 물 계면의 상승 높이인 2.73 mm보다 충분히 크게 하여 판과 판의 거리를 40 mm으로 정하였다. SE-FIT을 통하여 계산된 물기둥의 형상 해석 결과는 Fig. 4, Fig. 5와 같다. Fig. 4에서는 개방 채널의 깊이가 1mm로 고정하고 채널 폭을 0.15 mm에서 2 mm까지 변화하였을 때의 물기둥 상승을 계산한 결과이다. 이론적 모델링에서 가정한 바와 같이, 개방 채널에서의 물 접촉선 높이와 비교하여 개방 채널의 깊이와 폭이 작은 경우 물기둥의 형상은 사각기둥의 형태가 유지되고 있음을 확인할 수 있다. 하지만 채널의 폭이 증가할수록 물기둥 상단의 형상은 곡면이 되는 것을 관찰할 수 있다. w≥2d 구간에서는 식(4)에서 계산된 물기둥의 높이가 음수가 된다. 이 경우에는 식(2)의 가정인 물기둥의 높이 방향 1차원 해석이 불가능해지는 영역으로 물기둥의 단면 형상이 더 이상 사각형이 아닌 Fig. 2(c)와 같은 곡면(meniscus) 구조를 가지게 된다.

Fig. 4. Calculation results for various open channel cell widths, (a) 0.15 mm; (b) 0.25 mm; (c) 0.5 mm; (d) 1 mm; (e) 2 mm while the channel depth is fixed at d = 1 mm.

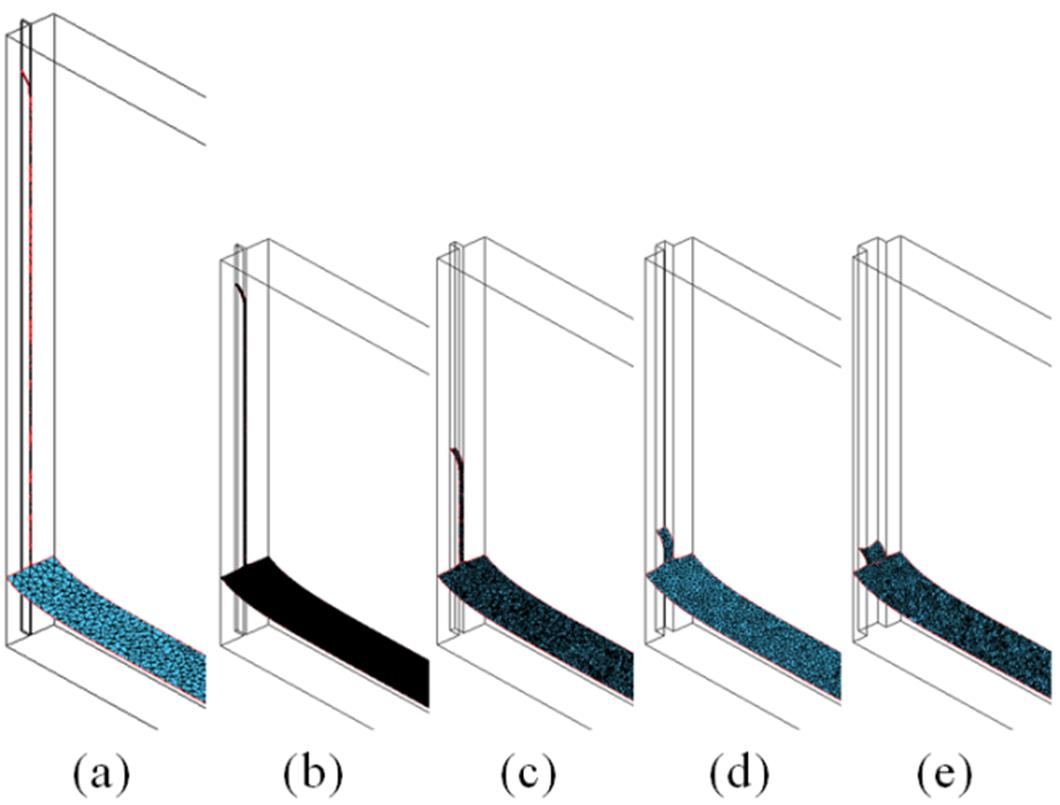
Fig. 5. Calculation results for various open channel cell depth, (a) 0.15 mm; (b) 0.25 mm; (c) 0.5 mm; (d) 1 mm; (e) 2 mm while the channel width is fixed at w = 1 mm.

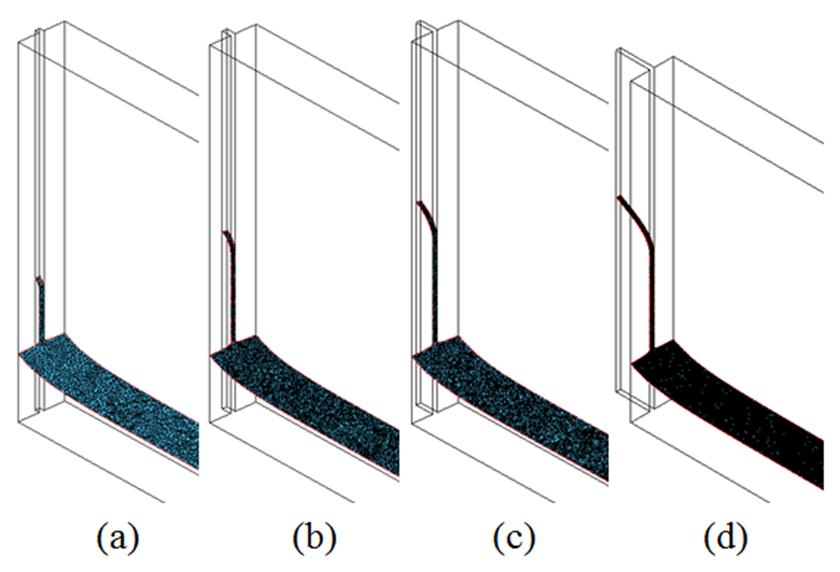
개방 채널의 폭을 1 mm로 고정한 후에 채널의 깊이를 변화시키면서 물기둥 상승을 계산한 결과에서는 채널의 깊이가 증가할수록, 물기둥 상부의 접촉선이 곡선이 되며 높이의 편차가 커짐을 확인할 수 있었다. SE-FIT 계산결과와 식(4)를 통한 이론 모델링 결과를 비교한 결과는 Fig. 6, Fig. 7에 표시하였다. SE-FIT 계산 물기둥의 높이는 최대와 최소 높이의 평균값으로 계산하였다. Fig. 6은 개방 채널 폭을 0.5 mm로 고정한 후 채널 깊이를 변화시키면서 식(4)와 SE-FIT를 통하여 계산된 결과값을 비교하였다.

Fig. 6. Comparison between the theoretical model from eqn. (4) and the calculation result from the SE-FIT simulation when the channel width is fixed at 0.5 mm.

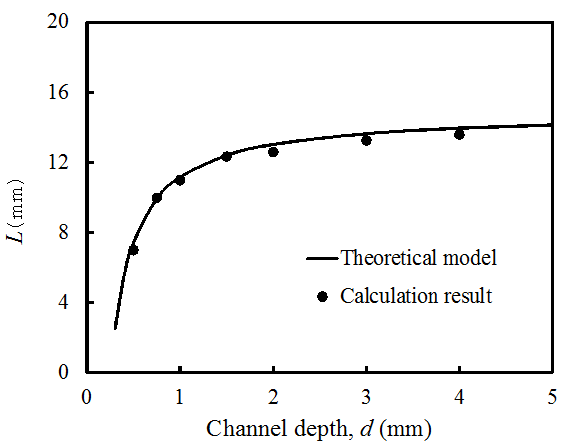
식(4)를 통한 이론적 계산과 SE-FIT을 통하여 계산된 물기둥의 높이는 전반적으로 잘 일치하고 있음을 확인할 수 있다. 채널 깊이가 증가함에 따라서 미소한 차이가 존재하며, 이는 SE-FIT에서 물기둥의 높이를 단순 최대와 최소 물기둥 높이의 산술평균값을 사용했기 때문에 이론값과 오차가 커진 것으로 판단된다. 물기둥 자유표면의 곡면 형상이 막힌면에서 공기에 노출된 개방면 방향으로 갈수록 그 기울기가 가파른 곡선의 형태를 갖기 때문에 산술평균값이 실제 물기둥의 높이를 과대하게 예측할 수 있다. 물론 채널 깊이가 증가할수록 물기둥이 자유표면 형상이 3차원 곡면을 띄기 때문에 이론식의 가정과 실제현상과의 차이가 커지며 이에 의한 이론식의 오차를 증가시키는 것으로 판단된다.

Fig. 7. Calculation results of the water column height by theoretical modeling(eqn. 4) and SE-FIT, depending on the channel width and depth.

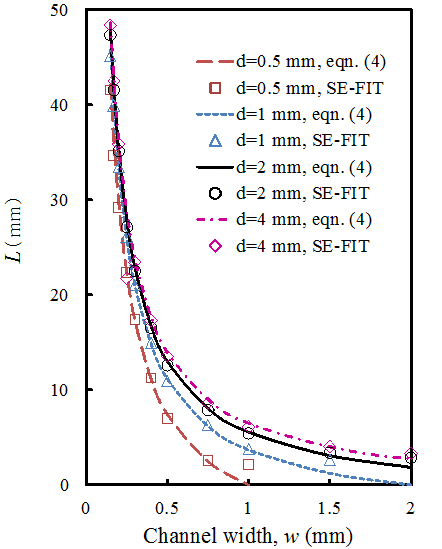
Fig. 7에는 채널의 폭과 깊이에 따라서 이론값과 SE-FIT 계산값을 비교하였다. Fig. 6과 마찬가지로 채널의 폭과 깊이가 증가할수록 물기둥은 낮아지며, 이론 예측값과 SE-FIT 결과의 차이가 벌어지는 것을 확인할 수 있다. 채널 폭이 0.5 mm 이하 구간에서 채널의 깊이와 상관없이 물기둥의 높이가 급격하게 감소하는 것이 관찰되며, 상대적으로 폭이 0.5 mm 이상에서는 물기둥 높이 감소폭이 둔화된다. 이를 통하여 물기둥의 높이에 채널의 깊이보다는 폭이 더 큰 영향을 미치는 요소임을 확인할 수 있다. 또한 이론 예측값과 SE-FIT의 차이는 폭과 깊이가 같거나, 폭이 깊이보다 큰 영역에서 오차가 무시할 수 없을 만큼 커지는 것으로 나타난다. 이는 물기둥 상부 표면의 접촉선의 형상이 보다 기울기가 가파른 곡선이 되어, 이론식의 가정이 맞지 않게 되기 때문이다. 결과적으로 이론 모델링 및 SE-FIT 해석 결과를 토대로 하면, 증발식 열교환기의 습채널 표면은, 0.5 mm 이하의 채널 폭을 가지도록 설계하는 것이 유리하다고 판단된다. 물론 물 속 혹은 열교환기 표면에 불가피하게 존재하는 먼지 등의 이물질 때문에 이론 결과와 실제 물기둥 간의 차이는 존재할 수 있다. 반면 개방 채널 깊이의 경우, 그 값을 지나치게 크게 설계하면, 열교환기의 부피가 지나치게 커질 수 있다. 또한 간단한 모델링을 통하여 구한 식(4)는 물기둥의 표면 형상이 사각형에 가까운, 채널의 폭이 깊이보다 작거나 같은 구간에서는 큰 오차 없이 사용할 수 있음을 확인하였다.

4. 결 론

본 연구에서는 수직형 증발식 열교환기의 수직방향 패턴 구조를 통해 표면에 친수 코팅과 같은 추가적인 가공없이 젖음도를 향상시킬 수 있는 형상에 대한 분석을 수행하였다. 다양한 개방 채널 형상에서 물기둥의 높이를 예측하기 위한 이론적인 모델링을 통하여 간단한 에너지 평형식을 도출하였다. 이론식의 결과값과 유한요소해석 기반의 SE-FIT 프로그램의 해석 결과를 비교하였다. 개방 채널 구조의 폭이 깊이와 비슷하거나 작은 구간에서는 이론 예측값이 SE-FIT 결과와 잘 일치하는 것을 확인하였다. 개방 채널의 폭을 0.5 mm 미만인 경우 물기둥의 상승 높이가 급격하게 증가하며, 이러한 구조를 활용하는 경우 보다 높은 열전달 효율을 갖는 친수성 열교환기의 습채널 구조를 설계할 수 있으리라 기대한다.