3.1 3차원 지중 모델

유한차분법(FDM; Finite Difference Method)을 적용하여 지중체(ground volume)를 수치 모델로 묘사하기 위해 우선 계산 격자를 직교 좌표(Cartesian coordinates) 내에서 설정해야 한다. 모델의 격자 크기는 수치 모델에서 중요한 역할을 하며 온도 구배가 크거나 물성치의 변화가 있는 곳의 격자 크기를 작게 설정하는 것이 일반적이다. 그러나 지나치게 촘촘한 격자는 계산 시간을 크게 증가시키는 원인이 된다. 본 연구에서는 지중열 교환기의 수평 및 수직 방향 격자를 Lee(6)가 제안한 방법(이하, CKLee 모델이라 부름)에 의해 구성하였으며 개략적인 개념도는 Fig. 1과 같다. 수직방향 격자는 최소 격자를 기준으로 의 증분 계수를 사용하여 구성하였으며, 수평방향은 보어필드(Bore-field)와 외부필드(far-field)를 구분하고 외부 필드에 대해서만 앞의 증분 계수를 적용하였다. 보어 필드는 향후 다수의 지중열 교환기를 모델링하기 위하여 별도로 설정한 것이다.

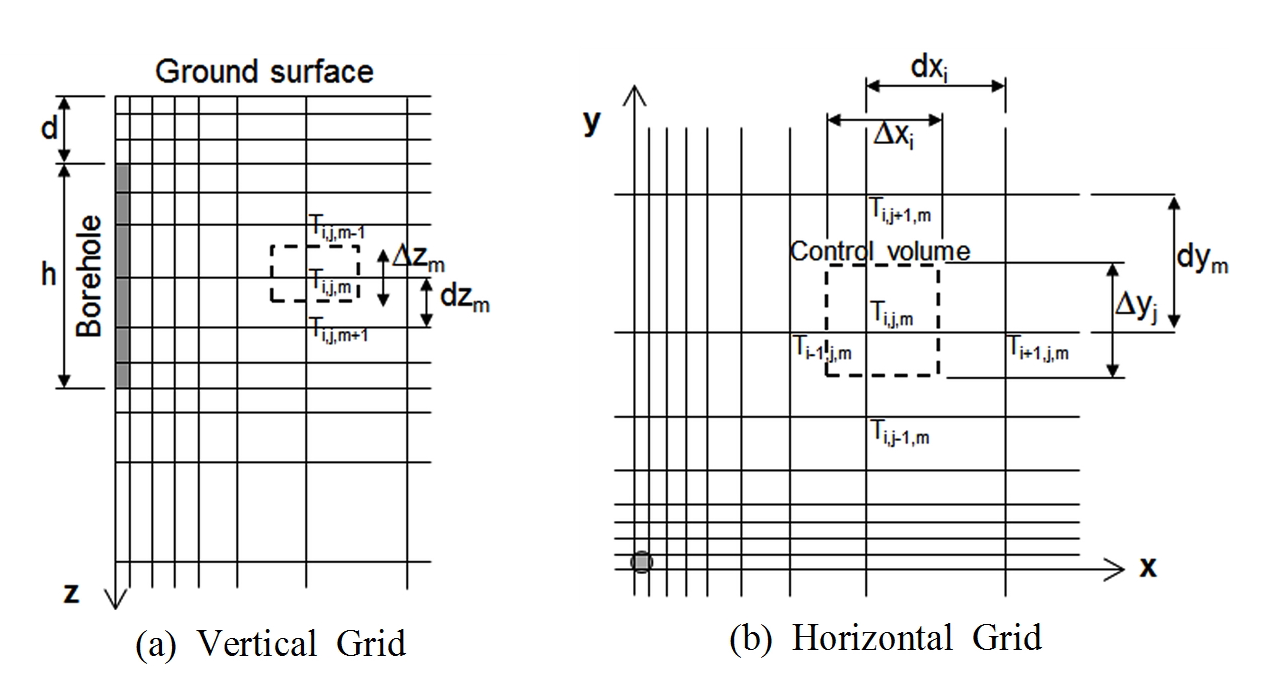
계산 격자 구성을 위한 프로그램 입력 값으로 보어홀 높이 구간(h)의 격자 개수(Nz)와 보어필드 면적만을 입력하면 식(1)로부터 자동적으로 최소 격자 간격을 계산하고 이로부터 전체 격자를 구획할 수 있도록 만들어졌다.

열전달 미분 방정식을 음해법(implicit scheme)을 이용하여 시간 이산화(discretization)하고, Fig. 1로 표현된 그리드의 각 절점 영역(control volume)에 대해서 공간 이산화하면, 대표 절점 Ti,j,m에 대한 이산화 방정식은 아래 식(2)와 같다. 모든 절점에 아래 식을 적용한 후 주어진 시간 간격마다 수렴할 때까지 반복 계산하여 전체 공간의 온도 분포를 계산할 수 있다.

여기서,

3.2 나내부 교환기 모델

본 연구에서는 위의 지중 모델과 결합할 교환기 내부(그라우트 및 유체) 모델로 열용량 모델을 제안하고 기존의 열 저항 모델과 비교하고자한다. Fig. 2(a)는 별도의 계산 격자가 필요 없는 열 저항 모델을 나타낸 반면, Fig. 2(b)는 원통형 그리드(cylindrical grid)를 이용하여 유체가 순환하는 U관에 해당하는 제어체적이 시스템과 동일 단면적 및 동일 거리를 유지하도록 격자 모양을 설정한 것이다. 내부 열용량 수치 모델은 원통형 그리드에서 정의가 편리하도록 유한 체적법(FVM; Finite Volume Method)을 이용하였다.

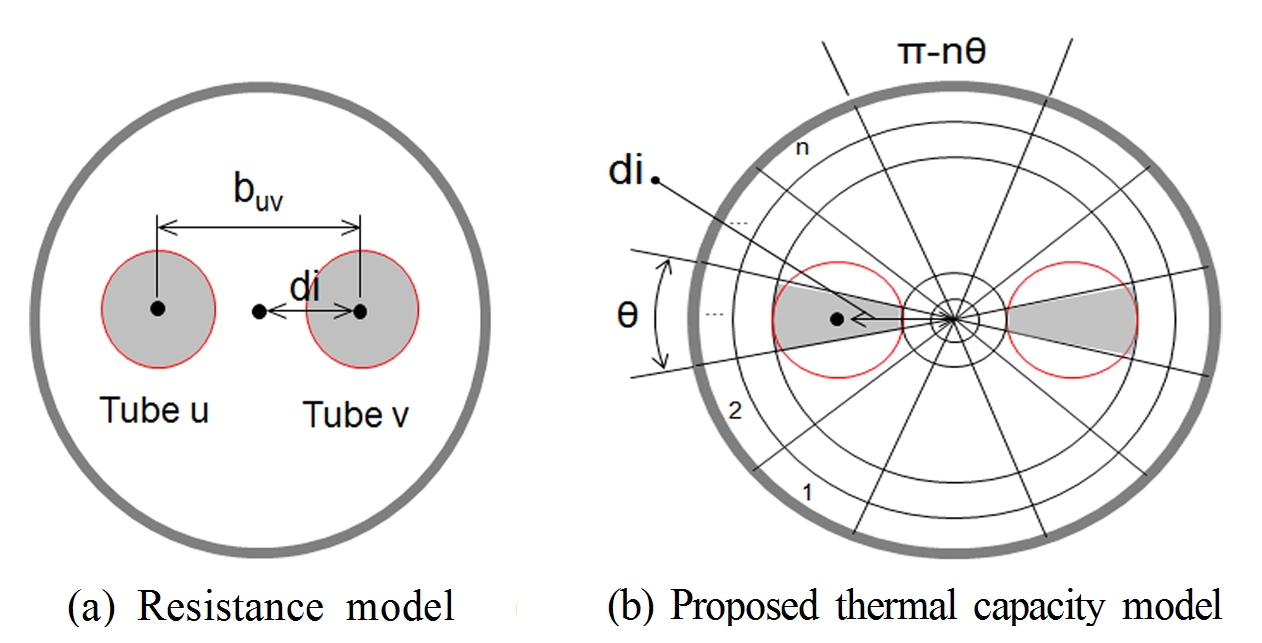
비교 대상인 열 저항 모델은 식(3)과 같이 Hellström(7)이 제안한 모델을 사용하였으며 이는 CKLee 모델에서 동일하게 사용되었다.

여기서,

Fig. 3과 같이 열용량 수치 모델에서 각 절점 사이의 열류를 계산하기 위해 열 저항 값을 계산해야 한다. 그림에서 보는 바와 같이 상대적으로 열용량 값이 작은 파이프는 격자 구성에서 제외시키고 열 저항 값(Rp)만을 계산에 포함시켰다.

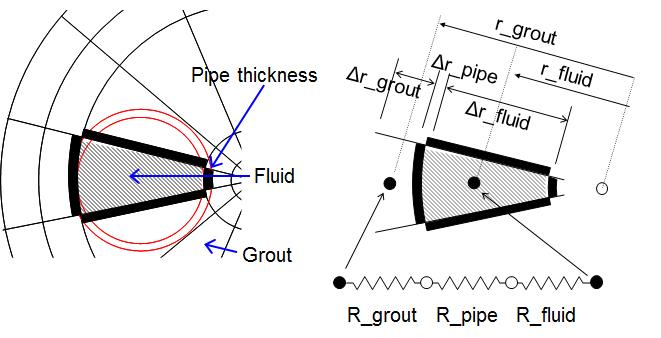
그림은 유체 절점과 바깥 방향 그라우트 절점 사이의 통합 열 저항(Rtot) 계산 방법을 나타낸 것이다. 식(4)는 직렬로 구성된 각 열 저항 값의 계산식을 나타낸다.

여기서,

위와 같은 원심 방향에 추가하여 원주방향 열 저항 Rθ(= Δθ×r/(kgΔzΔr))을 고려하면 원통형 그리드에서 각 절점의 이산화 방정식을 식(2)와 유사한 방식으로 정의 할 수 있고 아래식과 같다.

여기서 하첨자 k와 l은 각각 원통형 그리드의 원심(r) 및 원주방향(θ) 격자 지표를 나타내며 우측 분자의 각 항은 위에서 정의한 열 저항 값으로 계산된 방향별 열류를 나타낸다. 이 때 원통형 그리드가 U관의 상하류 지관 속 유체를 나타낼 때는 식(5)와 같이 유체 순환에 의한 열류 $q_f^{*}$를 계산에 포함시킨다.

3.3 모델 결합 알고리즘

위에서 정의한 지중 모델과 교환기 내부 모델을 결합하기 위해서 보어홀 벽의 온도(Tb)와 열류(W)를 수렴할 때까지 반복 계산(iteration)하는 방법을 사용한다. 앞서 언급한 바와 같이 각각 FDM과 FVM 방법을 이용하였기 때문에 높이에 따라 두 모델을 결합하는 방법은 Fig. 4와 같이 다소 복잡하다.

수직 z축 방향으로 두 모델은 격자 절점과 격자 중앙 점으로 각각 제어체적 중앙점이 다르므로 결합 시 수직방향 평균 값을 이용하였다. 그림에서 우측 교환기 내부 모델의 원주 방향 평균 열류를 W(t,z)라고 할 때 지중 모델의 각 절점 n°1, n°2, n°3, n°4에 대입되는 열류 값은 이웃하는 제어 체적의 열류 W(t,z-1)와의 체적가중 평균 값( $\overline{W}$(t,z))을 사용하며, 이 값은 4개의 절점에 동일하게 나누어서 입력하게 된다. 이 때 원통형 확산으로 계산된 열류를 직교 좌표에 적용시키기 위한 보정 계수가 필요하며 이를 부하율(load factor)이라고 표시하였다. 본 연구에서는 CKLee가 제안한 값인 1.047을 사용하였다. 이 계수는 지중열 교환기 근거리 계산 엄밀 해인 CHS(Cylindrical Heat Source)모델과의 비교를 통해서 얻어진 값이다. 마찬가지로 내부 교환기 모델의 경계 조건이 되는 보어 홀 벽 온도 Tb는 지중 직교 좌표에서 8개 절점의 평균 온도인 $\overline{\mathrm{Tb}}$(Fig. 4 참조)를 사용하였다. 이와 같은 반복 계산 과정은 Gauss Seidel 방법을 이용하여 계산 속도를 높였으며 두 모델 결합 시 수렴 조건은 으로 설정하였다.

4.1 시뮬레이션 조건

본 연구에서 제안한 모델을 검증 및 평가하기 위해서 내부 열용량 부분 및 모델 결합 방법을 제외하고 대부분의 모델링 방법을 차용한 CKlee 모델을 기준 모델로 선정하였다. table 1 은 사용된 지중 및 지중열 교환기 물성치와 시뮬레이션 조건을 나타낸 것이다.

시뮬레이션 입력 값을 위해 식(6)과 같이 시간 간격마다 지중열 교환기 입구 측 유체 온도를 설정 지중 부하 Q로부터 계산하여 모델에 대입한다. 본 연구에서는 Q = 4,000 W의 값을 적용하여 입구 측 유체 온도를 계산하였으며 이는 길이 당 36.3 W/m의 등가 열류 값을 나타낸다. 지중 부하 Q는 건물의 냉난방 부하를 열펌프의 성능계수로 환산한 값으로 지중열교환기가 감당해야 할 부하를 말한다.

식(7)은 설정 지중 부하 Q를 일정 주기로 적용하여 유체 온도를 입력했을 때 실제 지중열 교환기 통해 전달되는 열류 Qb를 계산하는 식이며, 이로부터 Qb/Q로 표현되는 부하 응답률(load ratio)을 정의할 수 있다. 이로부터 모델의 반응 패턴을 확인할 수 있다.

4.2 모델 검증

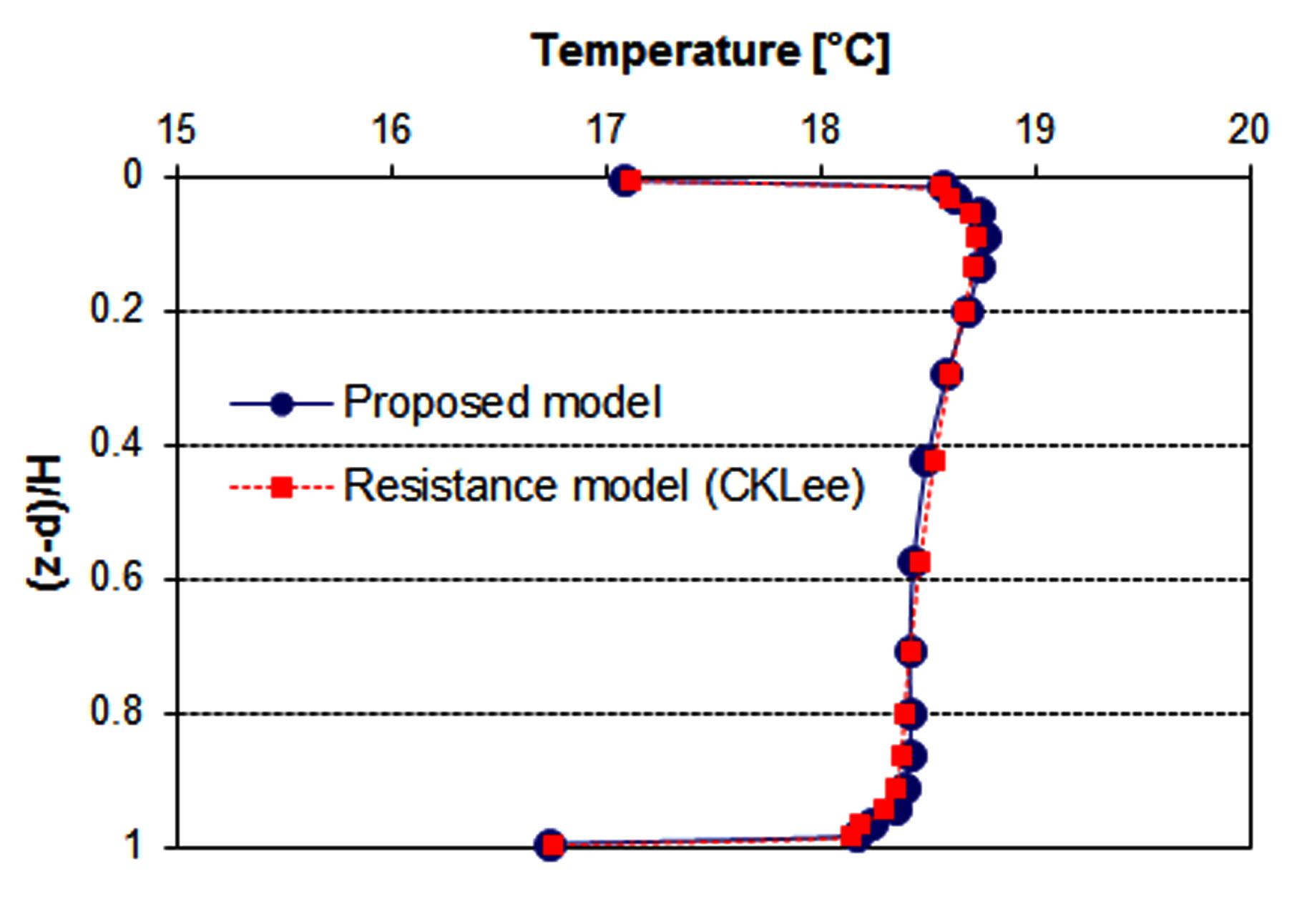
우선 모델의 검증을 위해 설정 부하 Q가 지속적으로 주입되었을 때에 지중 교환기 벽체 온도( $\overline{\mathrm{Tb}}$ (Fig. 4) 변화를 기준 모델과 비교하였다. Fig. 5는 연간 시뮬레이션으로 얻어진 높이에 따른 를 무차원수로 표현한 것이다. 그림의 각 점은 격자 구획에 따른 절점을 나타낸 것으로 보어홀 양 끝단으로 갈수록 격자 간격이 좁아져 데이터가 많은 것을 확인할 수 있다. 비록 내부 열 교환기 부분을 서로 다른 모델로 구성하였지만 일정한 지중 부하를 지속적으로 적용했을 때 두 모델은 매우 유사한 열적 거동을 나타낸다.

마찬가지로 Fig. 6에서 보는 바와 같이, 전체 적용 부하 Q에 따라 보어 홀 높이에 따른 부분 부하도 거의 동일한 결과를 보여주고 있다. 이는 지속적인 부하를 적용할 때 내부 열용량 모델의 중요성은 크지 않다는 것을 말해 준다.

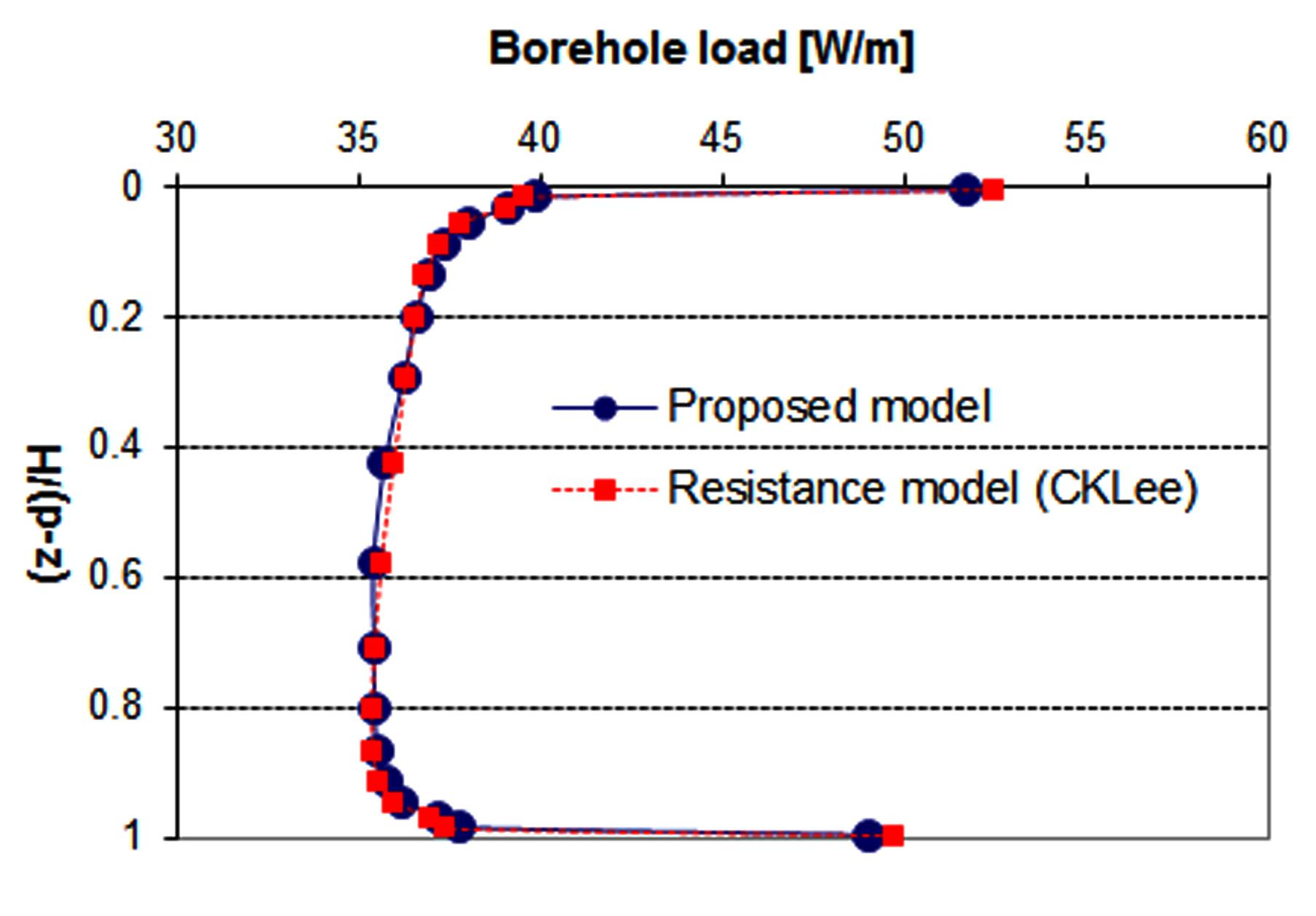
Fig. 5 및 Fig. 6의 결과는 제안 모델의 수치 검증 결과를 나타내기도 한다. CKLee 모델은 이미 충분한 수치 검증 과정을 통해 개발되었을 뿐 아니라 실증 연구에도 다양하게 활용되고(8) 있다.

4.3 내부 열용량 영향

식(6)에 의해 동일한 부하 Q를 두 모델에 적용시킬지라도, 지중열 교환기 내 열용량 효과에 의해 두 모델 사이의 반응 속도에 차이가 발생하는 것이 일반적이다. 앞선 결과는 일정한 Q를 지속적으로 주입한 결과로 부하가 적용된 초기 몇 시간을 제외하고는 반응 속도가 결과에 미치는 영향은 거의 없었을 것으로 예상된다.

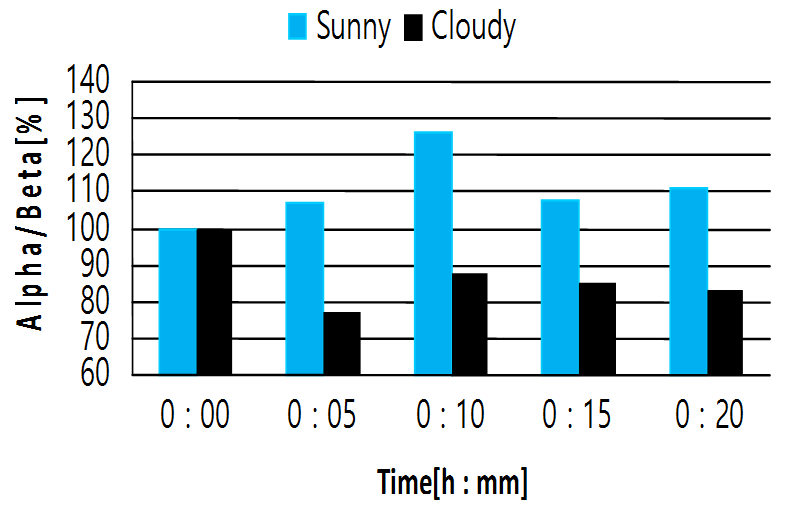
열용량 영향을 확인하기 위해서 12시간 주기로 Q를 적용시키고 교환기를 통해 전달되는 총 열류를 측정하여 매시간 부하 응답률(Qb/Q)을 계산하였다. 다음의 두 그림은 그 결과를 나타낸다. Fig. 7은 두 모델의 서로 다른 부하 응답률을 나타낸 것으로, 비교 대상이 되는 CKLee 모델의 경우 제안 모델에 비해 빠르게 응답하는 경향을 가지고 있다. 이는 내부 열용량을 고려하지 않는 모델에서 나타나는 일반적인 현상이다. 제안 모델의 경우 부하 적용 시 보다 느리게 반응하고, 내부 교환기 모델의 축열 효과로 인해 부하 미적용 구간에서도 상대적으로 큰 Qb 값이 존재한다.

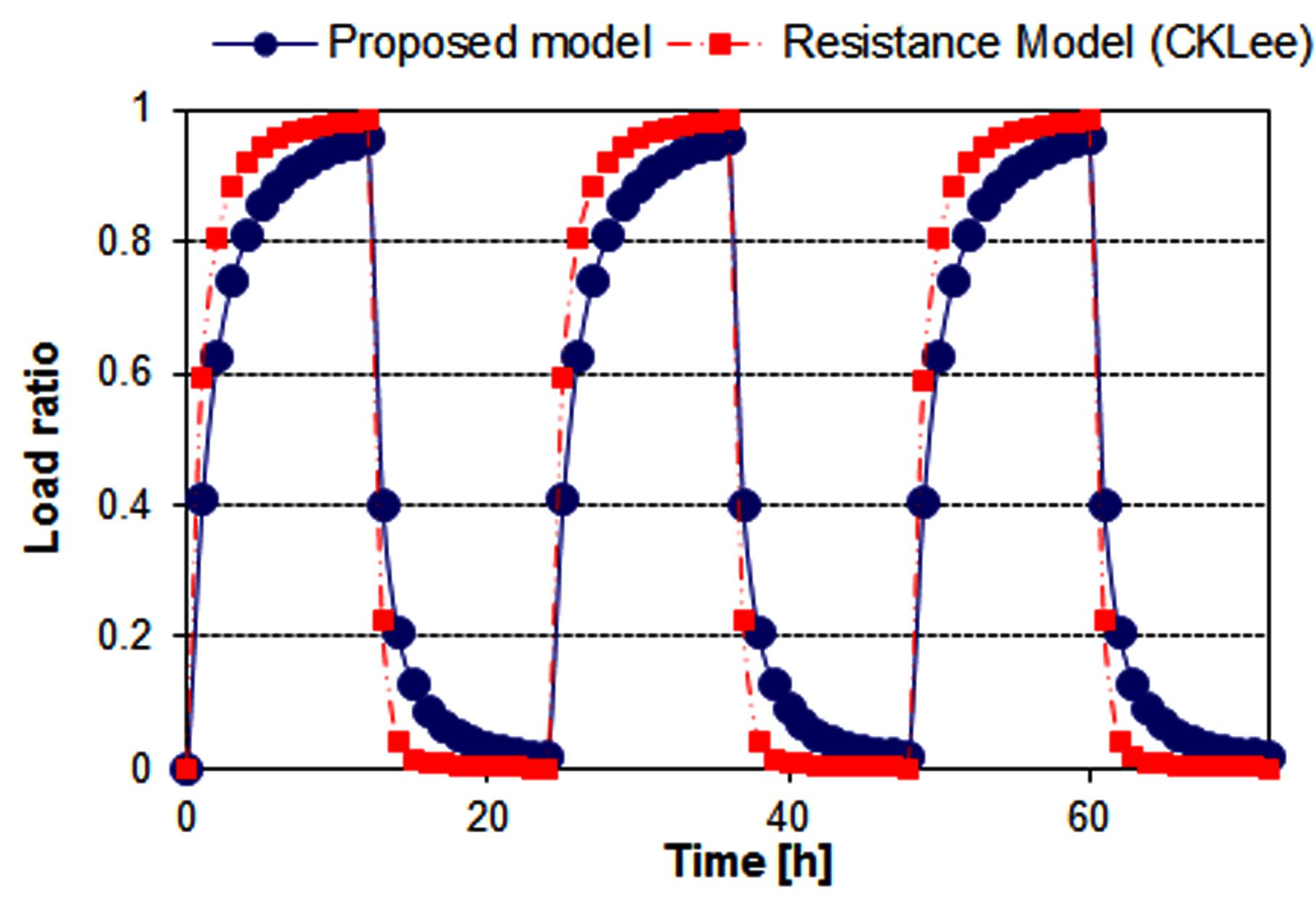
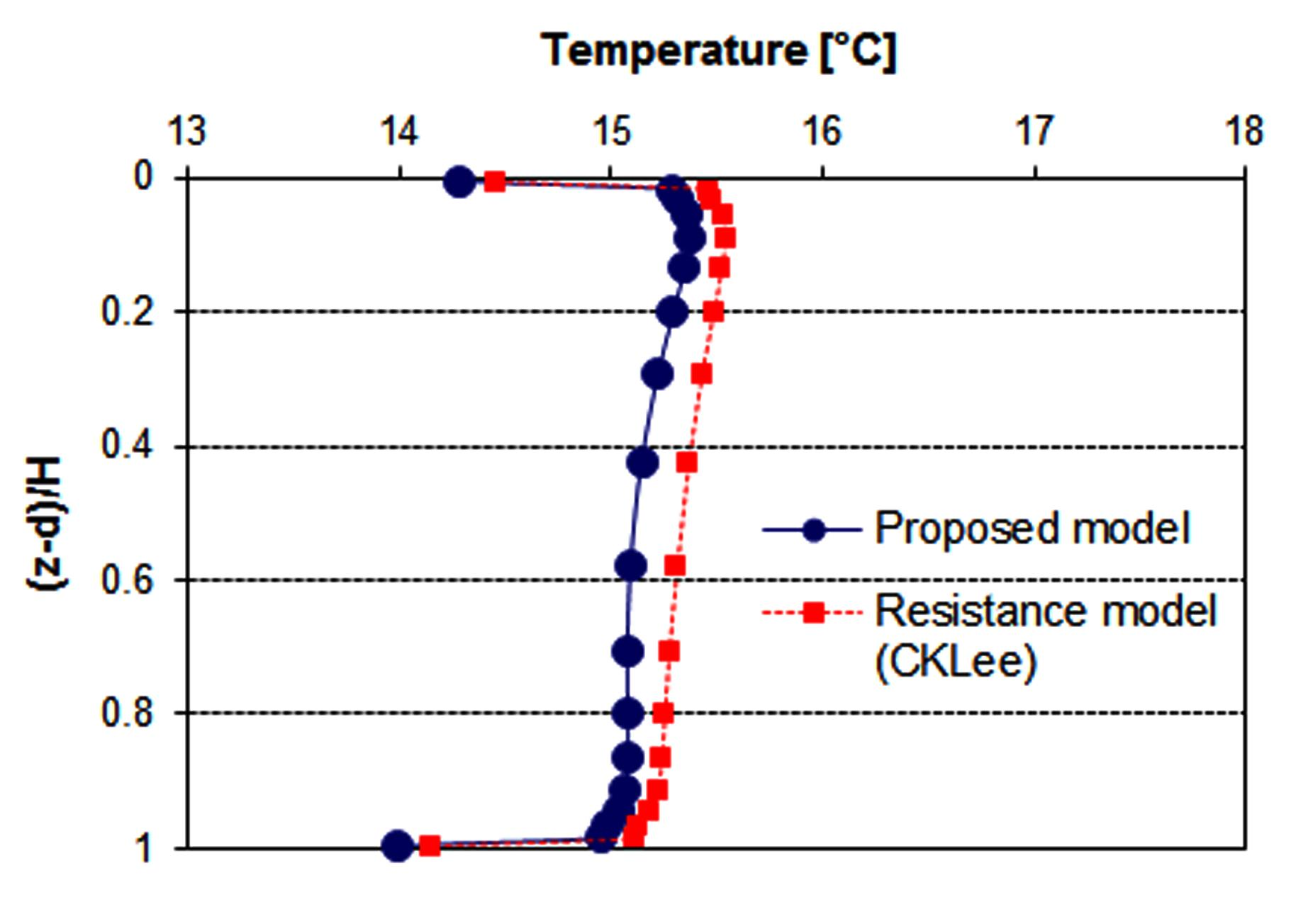
Fig. 8은 부하 응답률의 차이(Fig. 7)가 결과적으로 지중열 교환기 주변 온도 차이를 만들어내는 것을 보여주고 있다. 테스트 케이스에서는 초기 지중온도(10°C) 대비 상승 온도 약 5°C 중 0.3°C의 수준으로 약 6%의 온도 차이를 보이고 있다.

결과적으로 Fig. 7~Fig. 8를 통해 열용량 효과에 따른 모델의 응답 속도와 보어 홀 벽체 온도 차이가 발생하는 것을 확인할 수 있었다. 이는 각각 제어 전략 수립 및 장기 시뮬레이션을 이용한 상세 설계에서 중요한 인자가 된다.