1. 서론

최근, 건축물이 고층화, 대형화됨에 따라 건물의 효율적 운용을 위해, 신재생에너지 활용 및 축열조, 히트 펌프 등 다양한 에너지 절약적인 설비 시스템이 적극적으로 도입되고 있다. 하지만, 고효율 기기의 사용이 항상 최고의 에너지 절약 효과를 나타내지는 않으므로, 에너지 생산량 및 경제성을 고려한 최적 설계가 필요하다(1). 한편, 건물의 성능을 좌우하는 열원 시스템의 설계 단계에서는 대상 건물의 특성에 맞는 열원 선택 및 설비 시스템의 용량과 대수 분할, 기기 효율, 에너지 효율적 제어 방식 채택 등 과도한 설계 변수들과 제약들을 포함하고 있어 최적화에 어려움을 겪고 있다.

이를 해결하기 위해, 최적화 알고리즘을 이용한 설비 시스템의 최적 설계 방법에 관한 연구들이 국내외에서 활발히 이루어지고 있다.(1-5) Ooka and Komamura(1)는 유전자 알고리즘(GA : Genetic Algorithm)을 이용하여 에너지 시스템의 1차 에너지 사용량을 최소화하는 최적 설계 방법을 제시하였고, 연구 결과를 통하여 제안한 최적 설계 법의 유효성을 검증하였다. 나아가, Kayo and Ooka(2)는 에너지 시스템 최적화 연구에 사용된 유전자 알고리즘의 제어 파라미터 값을 케이스스터디를 통해 검토하였으며, Seo et al.(3)은 주거 건물의 설비 시스템을 대상으로 최적화 설계 수법을 제안하고 에너지 효율적 설계를 도출하였다. 또한, Kong et al.(4)은 유전자 알고리즘 외에 파레토 기반 분석방법을 적용하여 에너지 시스템의 다목적 최적 설계를 이루었으며, 최적해군으로 선정된 결과를 활용하여 실제 설계에서 의사결정 요인으로 활용되는 방안을 제시하였다. 하지만, 통상적으로 건물의 생애 주기 동안 건물의 성능에 영향을 미치는 에너지 시스템의 내용연수는 20년 이상일 수 있고,(5) 기기의 LCC(Life Cycle Cost)를 최적 설계에 반영한 연구는 부족하며, 냉방부하가 크게 발생하여 에너지 효율적 운용이 시급한 오피스 빌딩을 대상으로 정량적 부하 분석을 통한 최적화 연구는 드물다.

따라서, 본 연구에서는 오피스 빌딩의 효율적인 에너지 시스템 설계를 위해, 동적 에너지 시뮬레이션을 이용해 냉난방 부하 프로파일을 계산하고 iSIGHT 툴을 기반으로 한 유전자 알고리즘을 활용해 최적 열원설비 용량 설계 및 운전 계획을 도출하는 것을 목적으로 한다. 본 논문에서는 건물 에너지 시스템의 20년 LCC 및 초기 투자비용, 에너지 비용 최소화를 목적으로 하는 다단계 최적화 설계 수법에 대해 서술한다.

2. 최적화 방법

2.1 최적화 방법의 개요

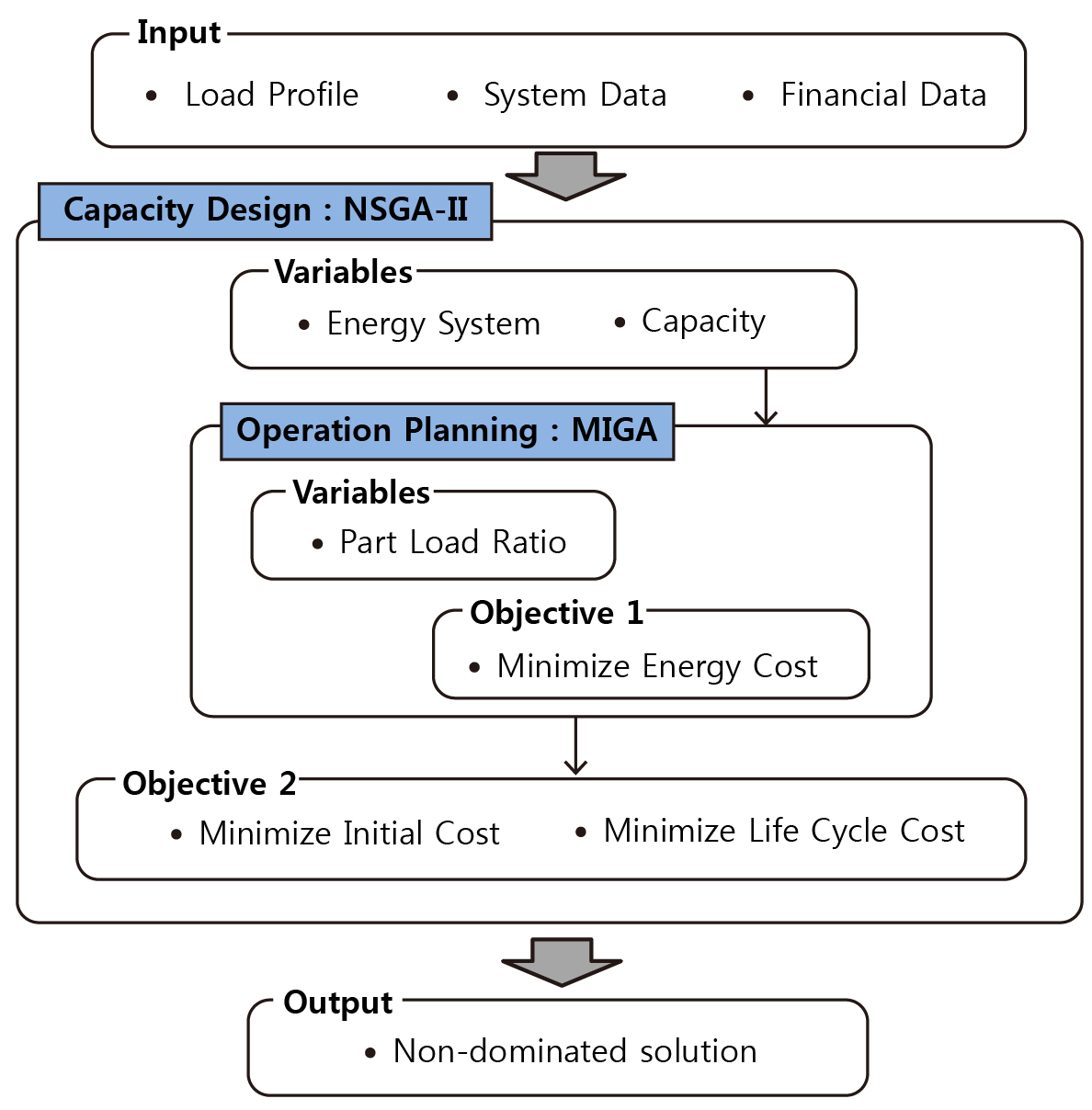
본 연구에서는 건물의 최적 열원설비 시스템 설계를 위해 유전자 알고리즘을 이용한 다단계 최적화 수법을 제시하고자 하며, Fig. 1은 본 연구에서 제안하는 다단계 최적화 프로세스를 나타내고 있다. Fig. 1에 나타난 바와 같이, 최적의 시스템 용량 설계를 위해 시스템의 초기투자비용과 LCC를 목적함수로 고려하는 NSGA-Ⅱ(Non-dominated Sorting Genetic Algorithm)를 이용하고 선정된 시스템 조합의 효율적 운영 방법을 계획하기 위해 MIGA(Multi-Island Genetic Algorithm)를 활용하는 2단계 프로세스로 구성되어 있다. 이 방법은 다양한 설계 변수가 존재하고 부분적 제약들을 포함하게 되는 경우, 부분적 문제를 처리한 뒤 통합하여 전체 문제를 해결하는 방법이다.(6) 따라서, 에너지 시스템의 용량과 기기의 부하율을 변수로 하여 에너지 비용이 최소화되는 운전 계획을 도출하고 LCC 및 초기 투자비용을 산출한다. 에너지 시스템의 설계 용량은 대상 건물의 냉난방 최대 부하를 만족하도록 조합하며, 선정된 시스템 조합의 에너지 절약적인 운전 계획을 검토하기 위하여 설계 대표일 4일(1월 : 난방 피크일, 5월 : 냉방 중간기, 8월 : 냉방 피크일, 11월 : 난방 중간기)의 냉난방 부하 프로파일을 대상으로 에너지 비용을 최소화하는 하나의 최적 운전 방법을 도출한다. 최적 운전법을 바탕으로 각 설계 대표일은 60일간의 운전을 대표한다고 가정하여 연간 에너지 비용을 산출하고, 최종 선정된 에너지 시스템의 초기 투자비용과 LCC가 최소화도록 최적화 프로세스를 진행한다. 다목적함수를 처리하기 위해 파레토 분석 기법을 이용하여 다수의 최적 해집단을 도출한다. 도출된 해집단은 다양한 최적 에너지 시스템 설계 방법을 제시할 수 있다.

Fig. 1. Outline of optimization.

2.2 목적함수

본 연구에서 제안하는 최적화 프로세스는 다수의 에너지 시스템 설계 조합과 각각의 설계안에 해당하는 하나의 최적 운전 방법을 제시하기 위해 총 3개의 목적함수를 이용하였다.

2.2.1 초기 투자비용

본 연구에서 건물 에너지 시스템은 냉방을 위해 터보식 냉동기(TR)와 히트펌프(HP), 난방을 위해 가스보일러(GB)와 히트펌프(HP)를 고려하였다. 본 논문에서는 기기별 최대 2대 적용 가능하며, 기기 용량에 따른 초기 투자비용은 한국 유통 물가 인터넷에서 거래되는 견적단가를 기준으로 책정되었다. table 1 은 본 논문에서 고려한 기기 종류와 용량에 따른 초기 투자비용을 나타낸다.

Table 1. Capacity and Price of each energy system

Turbo Refrigerator(TR)
Capacity	490	543	630	700	823
Price	74,000	78,560	81,420	85,320	88,640
Heat Pump(HP)
Capacity	100	200	400	600	800
Price	55,752	74,336	92,920	111,504	130,088
Gas Boiler(GB)
Capacity	41	122	204	285	366
Price	950	2,850	4,750	6,650	8,550

Unit : Capacity(kW), Price(thousand-won).

2.2.2 노즐각도변화에 의한 유동특성

본 연구의 에너지 비용은 부하에 따른 에너지 요구량에 대하여 기기별 소비되는 1차 에너지 비용을 의미한다. 에너지 비용을 산출하기 위해, 1차 에너지 소비량은 기기별 부분부하율(PLR)에 따라 달라지는 시스템 효율(COP)을 통해 계산되며, 식(1)과 같이 표현된다.

(1)

$E=\frac{Q_{load}}{COP}$

기기별 시스템 효율(COP)은 선행연구(1)를 참조하여 Fig. 2와 같이 부분부하율에 따른 성능 곡선으로 도식화하였고 2차 다항식의 추세식을 도출하여 계산식에 활용하였다. 여기서, 기기별 부분부하율(PLR)은 운전 계획 최적화의 변수로 0부터 1까지 0.2단위로 정의했다. 기기별 1차 에너지 소비량은 열원별 단가를 적용하여 에너지 비용을 산출하였고, 본 연구에서는 전기와 가스를 열원으로 사용하였다. 전기요금은 한국전력공사에서 제공하는 일반용 전력(을) 전기요금표를 기준으로 계절별, 시간대별 전력량 요금을 산출하였으며, 가스요금은 한국가스공사에서 제공하는 업무난방용 도시가스요금을 적용하여 계산하였다.

Fig. 2. Performance curve of energy system.

2.2.3 Life Cycle Cost

최적 설계 방법을 통해 제안하는 건물 에너지 시스템의 LCC는 내용연수 20년으로 가정하여 현가법(NPV : Net Present Value)을 통해 산출하였다. 본 논문에서는 열원 시스템의 LCC 요소로서 크게 초기투자비용, 에너지비용, 유지관리비용을 반영하였다. 초기투자비용과 에너지비용은 제2.2.1절과 제2.2.2절에서 언급한 바와 같이 계산되며, 유지관리비용은 Paek의 연구(7)를 참고하여 각 시스템의 보수주기는 5년, 보수율은 초기설치비의 2%로 설정하였다. 계산은 다음의 식(2)와 같이 반복비용과 비반복비용으로 나누어 현재 가치로 환산하는 방법이다. 여기서, 실질할인율(i)은 선행연구를 참조하여 3.4%를 적용하였다.(8)

(2)

$NPV=\frac{F}{i(1+n{)}^n}+\frac{A\left[\right(1+i)-1]}{i(1+i{)}^n}$

2.4 파레토 분석

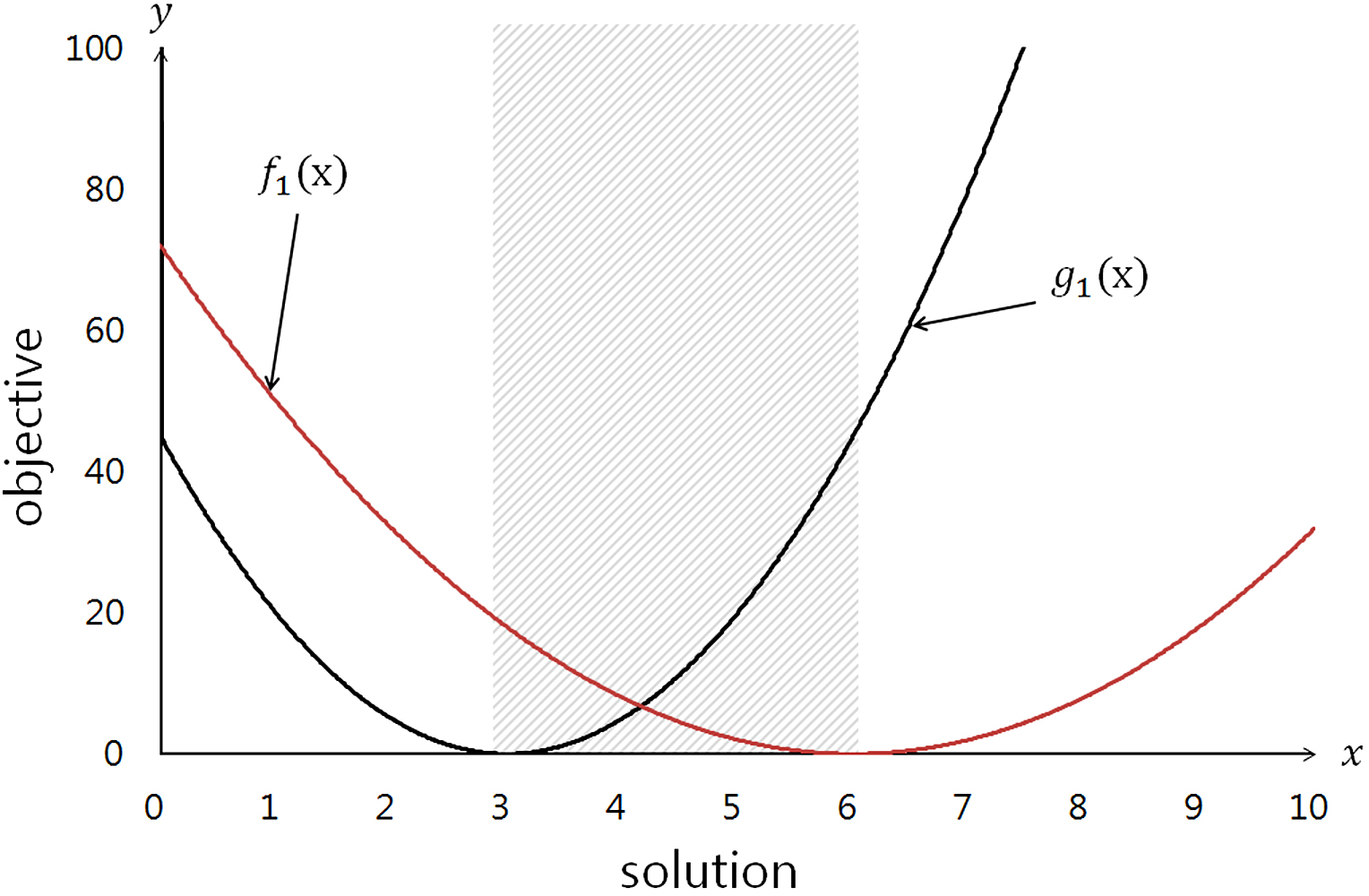
본 연구에서 이용한 NSGA-Ⅱ 모델은 다목적 함수를 처리하며, 이 경우 다수의 목적함수들을 동시에 만족하는 하나의 최적해는 존재하지 않는다. 따라서 유전자 알고리즘과 함께 파레토 분석 기법을 병행하여 파레토 최적해 개념을 도입하였다. 파레토 최적해는 다수의 해집단으로 구성되며, 최소 하나의 목적함수 값을 증가시키지 않고는 다른 목적함수 값을 감소시킬 수 없을 때 이에 상응하는 가변영역의 해를 파레토 최적이라 정의한다.(6) 예를 들어, Fig. 3에 나타난 바와 같이 목적함수가 f₁와 g₁로 주어진 경우 빗금 친 부분의 모든 값이 파레토 최적해가 된다. 또한, 본 논문에서 사용된 NSGA-Ⅱ에서는 파레토 최적해를 생성하기 위해 목적함수와 함께 개체의 밀도 정보를 부가적으로 활용한 적합도 평가를 기반으로 한다.(9) 따라서, 본 연구의 최적화 기법을 이용해 다수의 최적 솔루션을 비교 검토할 수 있다.

Fig. 3. Pareto optimum solutions.

3. 분석 조건

3.1 대상 건물 및 부하 프로파일

Fig. 4는 연면적 10,680 m²의 오피스 건물을 모델링한 것으로서 선행연구(10)를 참조하여 실내 조건을 설정하였고, 본 논문에서는 대상 건물에 대한 냉난방 부하 프로파일을 활용하여 최적화 분석을 진행하였다. 대상 건물이 서울지역에 위치하여 있다고 가정하고 TRNSYS 17을 이용하여 냉난방 부하 분석을 실시하였으며, 분석 결과 난방 피크 부하는 1월 16일 324.5 kW, 냉방 피크 부하는 8월 27일 735.6 kW로 산출되었다.

Fig. 4. Analysis office building model.

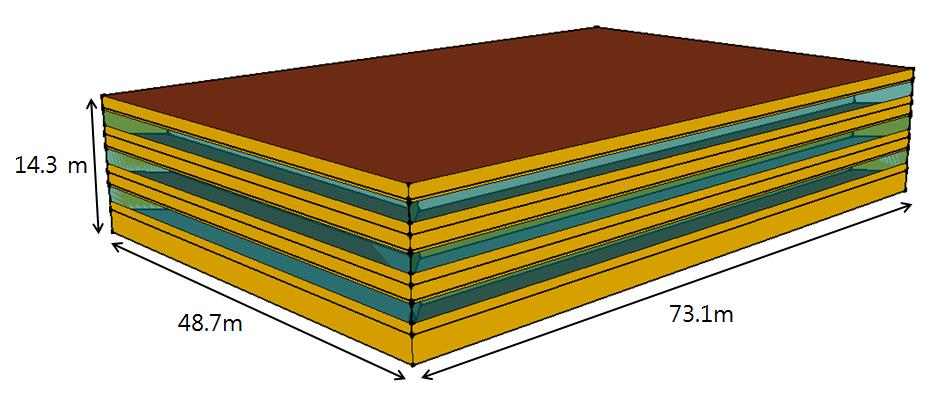
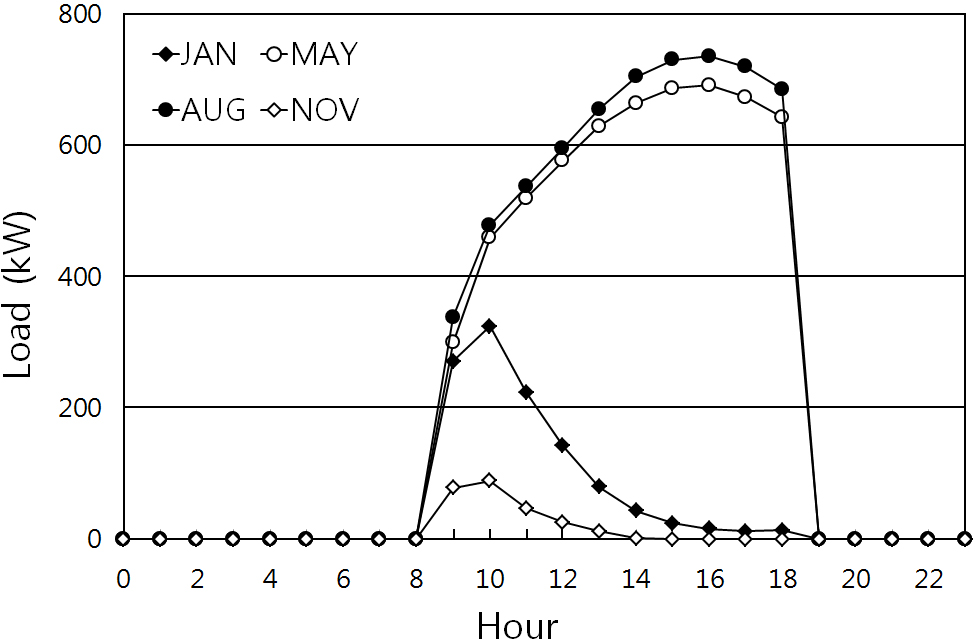
Fig. 5는 최적화 분석의 입력값으로 활용된 설계 대표일 4일의 부하 프로파일로서, 냉난방 피크일과 함께 냉방과 난방을 시행하는 5월과 11월 중간기 대표일을 선정하여 나타내었다.

Fig. 5. Load profile of representative days.

4. 최적화 결과

본 논문에서 총 1,728,000개의 케이스를 계산하여 선정된 오피스 건물 열원시스템의 최적 해집단은 table 4와 같다.

최적 해집단은 제약 조건을 만족하는 케이스들 중에서 적합도 수치 9인 개체들로서 Fig. 6에 나타난 바와 같이 균일하게 파레토 프론트에 분포되는 것을 확인할 수 있다. 또한, table 4에서 볼 수 있듯이 최적 해들은 유사한 시스템 조합 특성을 가지고 있다. 이는 시스템 설계 조합에 있어서 초기투자비용이 하나의 목적함수로 설정되어 냉방을 위해 터보식 냉동기를 이용하고 난방을 위해 가스보일러를 사용하는 것이 비용 효율적이기 때문이다. 한편, 유전자 알고리즘은 초기 몇 세대 안에 전역 공간을 탐색하여 근사해에 도달하고, 최적해에 수렴하는 특성을 가지고 있기 때문에 유사한 해집단을 나타내는 것으로 판단된다.

Fig. 6. Pareto front results.

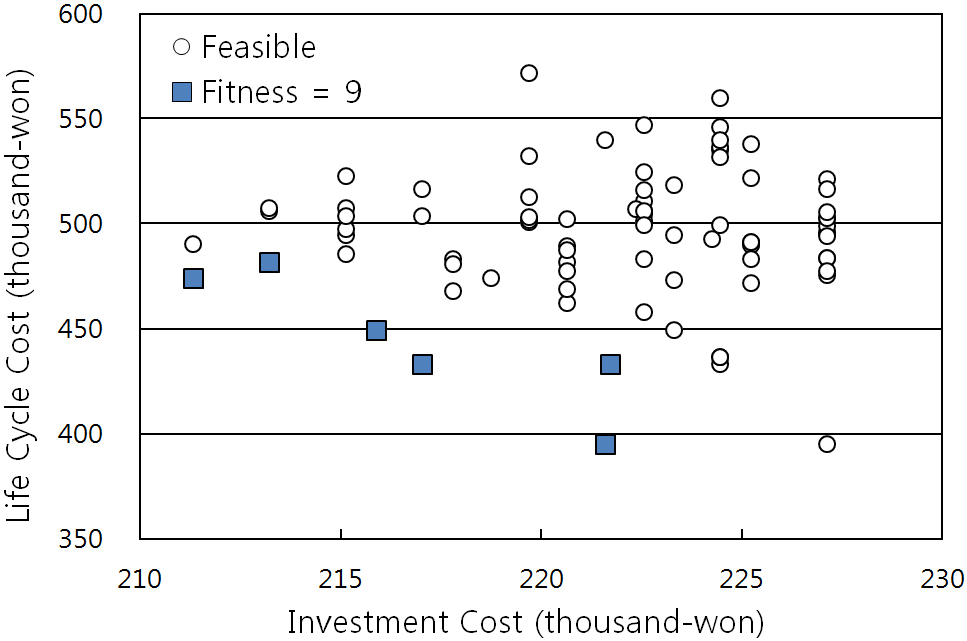
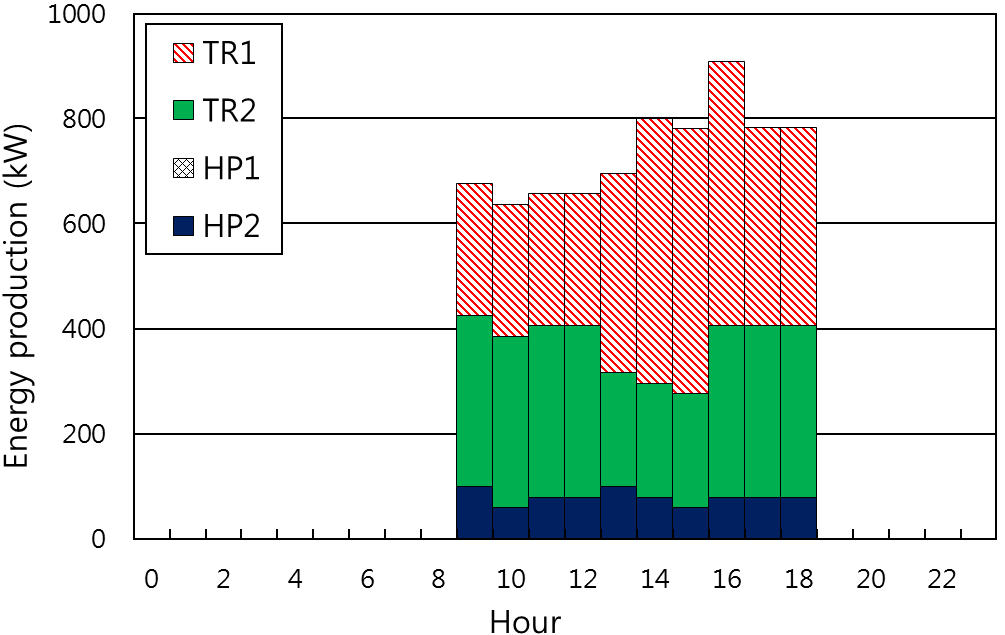
Fig. 7과 Fig. 8은 난방 피크일과 냉방 피크일의 열원시스템 운영 계획을 나타내는 것으로서, 최적 해집단 중에서 Alt-6을 이용하였다. 난방은 기본적으로 100 kW의 히트펌프 1대가 가동되고 난방에너지 수요량이 증가하는 9시부터 14시까지 용량이 다른 2대의 가스보일러가 운전하여 필요한 난방 에너지량을 생산하는 것으로 나타났다. 냉방의 경우, 난방 운전과 비교하여 상대적으로 공조 운전 시간 동안 에너지 요구량이 크게 발생하여, 냉방 열원시스템으로 선정된 용량이 다른 2대의 터보식 냉동기와 1대의 히트펌프가 항시 가동되었다.

Fig. 7. Operation plan of representative heating day.

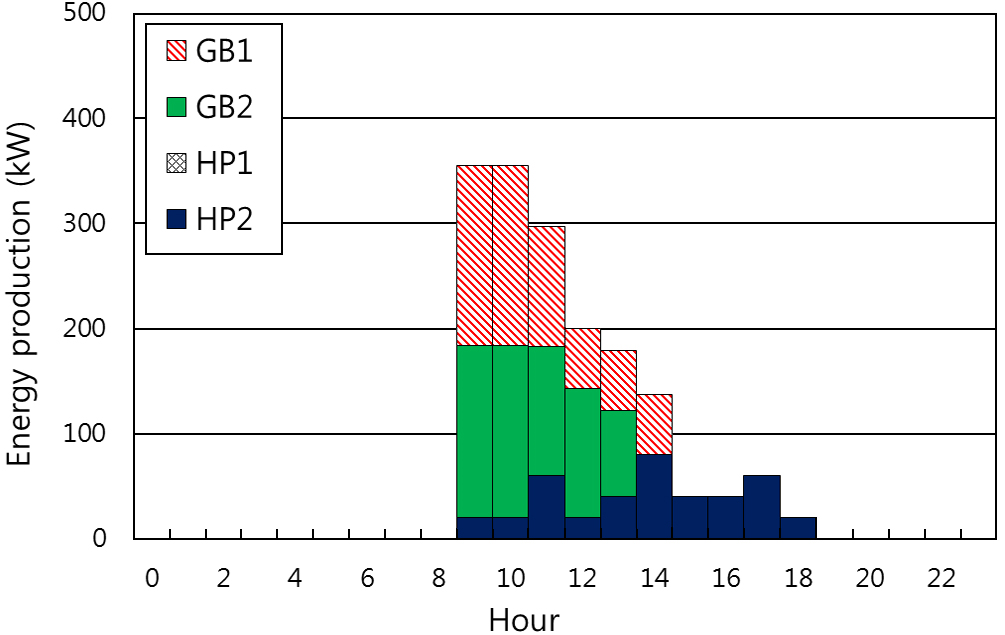
Fig. 8. Operation plan of representative cooling day.

5. 결 론

본 논문에서는 오피스 건물 열원시스템의 최적 설계 및 효율적 운영 방법을 제시하기 위해, 유전자 알고리즘을 이용한 다단계 최적화 수법을 제안하고 유효성을 확인하였다. 결론은 다음과 같다.

(1) 오피스 건물의 효율적인 열원시스템 설계는 방대한 설계변수와 비선형적인 기기 특성을 반영하기 때문에 해결 과정이 복잡하고 고비용이 소요되므로 최적화 알고리즘을 이용한 최적 설계가 필요하다.

(2) 본 연구에서 제안하는 다단계 최적화 수법은 동적 에너지 시뮬레이션을 이용해 계산한 부하 프로파일과 열원시스템의 성능곡선을 사용하고 iSIGHT 툴을 기반으로 한 유전자 알고리즘의 2단계 프로세스로 구성하여, 초기투자비용과 LCC를 최소로 하는 최적의 열원시스템 조합과 선정된 시스템의 에너지 비용이 최소화되는 최적의 운전 방법을 도출하였다.

(3) 오피스 건물을 대상으로 총 1,728,000개의 케이스를 분석한 결과, 6개의 파레토 최적 해집단을 확인하였고 열원시스템의 운영 계획을 통해 에너지 절약적 시스템 운영이 가능함을 확인하였다.

따라서, 본 연구에서 제안한 최적화 설계수법은 과도한 설계변수와 제약들로 인해 최적화 해결 과정이 어려운 상황에서, 유효한 방법으로 활용될 수 있는 것으로 판단된다. 하지만, 다수의 파레토 최적해들 중에서 일반적으로 가장 큰 효용값을 갖는 대안을 찾는 것은 고려되지 않았다. 향후, 최적 해집단의 우선수위를 결정하기 위해 결정론적 계획법을 적용한 연구를 진행할 것이며, 계산 시간을 고려해 효율적인 유전자 알고리즘 제어 파라미터 값을 검토할 예정이다.