Lee Donggyu
(이동규)
1
Park Sechang
(박세창)
2
Chung Dong-yeol
(정동열)
3
Kang Cheadong
(강채동)
4†
-
Geothermal Energy Technology Research Center, Chonbuk National University, Jeonju-si,
54896, Korea
(전북대학교 지열에너지연구센터)
-
Korea Construction Equipment Technology Institute(KOCETI), Gunsan-si, 54004, Korea
(건설기계부품연구원)
-
Thermal & Fluid System Group, Korea Institute of Industrial Technology(KITECH), Cheonan-si,
31056, Korea
(한국생산기술연구원 열유체시스템그룹)
-
Department of Mechanical Engineering & Geothermal Energy Technology Research Center, Chonbuk National University, Jeonju-si,
54896, Korea
(전북대학교 기계공학과&지열에너지기술연구센터)
Copyright © 2016, Society of Air-Conditioning and Refrigeration Engineers of Korea
keywords
Phase change material, Natural convection, Simultaneous, Charging and discharging, Computational fluid dynamics
키워드
상변화물질, 자연대류, 동시의, 축/방열, 전산유동해석
기호설명
T:temperature [℃]
H:enthalpy [kJ/kg]
g:gravitational acceleration [m/s2]
h:sensible enthalpy [kJ/kg]
L:latent heat [kJ/kg]
k:thermal conductivity [W/m·K]
φ:liquid fraction
ρ:density[m3/kg]
v, u:velocity[m/s]
μ:viscosity
하첨자
c:cooling
h:heating
in:inside
l:liquid
s:solid
ref:reference
PCM:phase change material
1. 서론
축열시스템은 열에너지 수요의 시간적 또는 양적 변동에 대응하기 위해 고안되었으며 대표적인 예로, 현열을 이용한 축열 방식과 잠열을 이용한 축열 방식
등이 있다. 축열 물질의 현열 변화를 이용하는 방식은 비교적 기술이 간단하여 손쉽게 이용할 수 있는 반면, 축열 밀도가 작아 축열 양의 규모가 커질수록
많은 양의 축열 물질과 축열 공간이 필요한 단점이 있다. 그러나 축열 물질의 잠열 변화를 이용하는 방식은 현열을 이용하는 방식에 비하여 축열 밀도가
커서 장치의 크기와 설치 공간을 줄일 수 있다. 이러한 장점으로 인해 잠열 변화를 이용한 축열 방식에 대한 관심이 증가되고 있다.
하지만 잠열 변화를 이용하는 축열 방식은 축열 물질을 가열/냉각하는 과정에서 상변화를 동반하기 때문에 열전달 현상과 열적 거동이 매우 복잡하다.
따라서 실험적 접근뿐만 아니라 수치 해석적 접근 방법을 이용하여 축열 물질의 열전달 특성 및 열적 거동을 확인하기 위한 많은 연구들이 진행되고 있다.(1)
특히 상용 전산유체역학(CFD : Computational Fluid Dynamics) 프로그램을 이용한 축열 물질(PCM : Phase Change
Material)의 상변화에 관한 해석은 계산영역 및 모델형상을 중심으로 이루어졌다. 계산영역은 크게 고정격자계나 이동격자계로 나누고 있으며, 충전된
PCM의 형상 및 경계형상(휜 부착 유무)에 따른 비교 연구 등이 진행되었다.
Brent et al.(2)은 유한체적법을 이용하여 융해 및 응고 과제에 대한 시뮬레이션을 진행하였으며 고정격자계에서 enthalpy-porosity method를 적용하여
액체와 고체 경계면에 대한 움직임과 온도 및 속도 정보를 획득하였다.
이동격자계에서 PCM의 상변화 해석은 해석과정 중에 격자를 재생성하거나 격자의 위치를 이동시킴으로써 고정격자계에서의 단점을 보완하여 해석 효율을
증대시켰다. Viswanath and Jaluria(3)는 PCM의 융해 및 응고과정에 대한 해석에 있어서 고정격자계와 이동격자계에 대한 비교 해석을 진행하여 온도분포와 부력을 포함한 유동장 형태를 파악하였다.
또한 다양한 형상에 충진된 PCM의 상변화 과정에 대한 많은 연구들이 진행 되었다. 직사각형,(4) 구형,(5) 원통구조,(6) 캡술형(7) 및 Fin의 유무(8)에 따른 열전달 특성 및 온도와 유동장 분포에 대한 분석을 진행하였다.
본 연구에서는 PCM이 충전된 축열조에서 열에너지를 저장하고 이용하는 과정에 대한 모사를 통해 실제 축열조 내부에서 열전달 시 발생하는 문제점을
파악하고자 하였다. 축열조를 모사한 직사각형 공간에서 동시 가열/냉각 조건을 가지는 PCM의 열전달 특성을 ANSYS FLUENT® 프로그램을 이용하여
자연대류를 고려한 상태에서 수치해석을 진행하였다.
2. 해석모델 및 지배방정식
2.1 해석모델
일반적으로 축열조 내부는 열에너지를 저장하기 위한 축열 물질과 축열 물질에 열에너지를 공급하기 위한 배관(축열 물질의 상변화 온도보다 높은 온도를
갖는 유체가 흐름)과 축열 물질로부터 열에너지를 빼앗기 위한 배관(축열 물질의 상변화 온도보다 낮은 온도를 갖는 유체가 흐름)으로 구성 되어 있다.
따라서 Fig. 1에서 보는 것과 같이 축열조 내부 구조 일부분을 모사하여 해석 모델을 구성하였다. 사각 공간(H×W = 0.1×0.1 m2)에서 좌우 경계면은 등온 조건을, 상하 경계면은 단열조건을 부여하였다. 사각 공간 내부는 table 1과 같은 열물성을 갖는 PCM이 모두 충전된 것으로 가정하였으며 초기 온도(Tin)는 80℃로 고정하였다. 또한 사각 공간의 좌측은 PCM에서 열에너지가 방출 되도록 하기 위해 경계면 온도를 PCM의 상변화 온도보다 낮은 온도를
갖도록 하였으며 사각 공간 우측은 PCM에 열에너지를 공급되도록 하기 위해 경계면 온도를 PCM의 상변화 온도보다 높게 하였다. 그리고 PCM이 충전된
사각 공간에는 y방향으로 중력이 작용한다. 자연대류를 고려한 상변화 현상을 분석하기 위해 ANSYS FLUENT® 프로그램은 비압축성, 비정상, 층류유동
상태에서 해석을 수행했으며 Energy equation과 solidification/melting model을 사용하였다. 또한 Boussinesq
근사를 이용하여 상변화 과정에서 PCM의 밀도를 정의하였으며 열 유동장 해석은 SIMPLE Algorithm 기법을 이용하여 수행했다.
Fig. 1. Schematic diagram of the analysis model, counter flow of rectanguler space simulates the thermal storage tank.
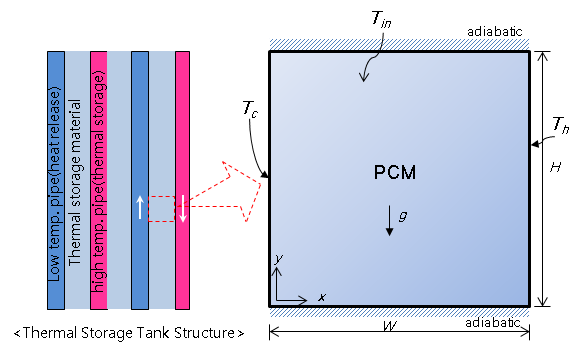
Table 1. Thermal properties of PCM
|
Item
|
value
|
|
Density(kg/m3)
|
2,180(1,950)
|
|
Specific heat(kJ/kg·℃)
|
2.25(3.77)
|
|
Thermal conductivity(W/m·℃)
|
1.3(0.657)
|
|
Latent heat(kJ/kg)
|
301
|
|
Viscosity(kg/m·s)
|
3.9×10-3
|
|
Melting temp.(℃)
|
78
|
2.2 지배방정식
PCM의 상변화 과정을 해석하는 동안 적용된 연속방정식(식(1)), 운동량 방정식(x방향-식(2), y방향-식(3)) 및 에너지 방정식(식(4))은 다음과 같다.
또한 해석과정 중 물질이 상변화하는 과정에서 열물성에 변화를 발생하기 때문에 고상, 액상 및 잠열구간(mushy zone)에서의 PCM 물성은 각
온도구간에서 다음으로 정의되는 액분율 φ를 이용하여 나타내었다.
따라서 PCM의 밀도, 열전도도 및 엔탈피는 각각 다음과 같이 정의하였다.
여기서 는 잠열의 변화량(Δ)을, L은 PCM의 잠열량이다.
일반적으로 유체 상태의 물질 내부는 온도차에 의한 부력으로 자연대류가 발생하며 이를 고려하기 위해 다음과 같은 Boussinesq근사식을 적용하였다.
또한 PCM이 충전된 2차원 사각 공간에서 상변화 시 부피변화와 y방향의 위치에 따른 운동량 변화는 고려하지 않았으며 사각 공간 경계인 벽면에서
액상 PCM의 속도 u, v는 점착(no-slip)조건에 의해 0으로 가정하였고 사각 공간에서 온도 변화에 관계없이 액상 PCM의 점성은 일정하다고
하였다.
3. 해석결과 및 고찰
사각 공간 내부가 액체 상태의 상변화 물질(초기온도 83℃)로 충전된 것으로 가정하고 좌․우 측면에 일정 온도 조건을 주었을 때 PCM의 온도분포
및 자연대류에 의한 유동 특성을 분석 하였다. table 2는 해석과정에 사용된 사각 공간의 온도 경계조건을 나타낸 것이다. 이 때 사각 공간의 상․하단은 단열조건으로 지정하였다.
Table 2. Boundary condition
|
Test No.
|
Tin[℃]
|
Tc[℃]
|
Th[℃]
|
|
1
|
80
|
63
|
adiabatic
|
|
2
|
80
|
73
|
93
|
|
3
|
80
|
63
|
93
|
|
4
|
80
|
63
|
83
|
3.1 PCM 응고과정
table 3은 사각 공간의 좌측 변을 63℃의 일정온도조건, 우측 변을 단열조건으로 고정하고(Test No.1) 사각공간 내부에 있는 액체상태의 PCM이 고체로
상변화되는 과정을 분석함에 있어서 사각 공간의 mesh size의 영향을 살펴본 결과이다. mesh size가 증가함에 따라서 사각 공간 내부의 모든
PCM이 고체로 응고되는 시간이 증가하였으며 수렴도가 개선되었다. 하지만 mesh size의 크기가 200×200 이후에는 큰 변화가 보이지 않았다.
이와 같은 결과를 바탕으로 모든 실험 조건에서 mesh size는 200×200으로 진행하였다.
Table 3. The effective of mesh size about analysis results
|
Test No.
|
Tin[℃]
|
Tc[℃]
|
Th[℃]
|
|
2
|
80
|
73
|
93
|
|
3
|
80
|
63
|
93
|
|
4
|
80
|
63
|
83
|
Fig. 2는 Test No. 1의 실험조건에서 사각 공간 내부에 있는 액체상태 PCM의 고체로의 상변화를 해석한 결과로 해석 시간 이후 1시간 경과 후의 온도분포
및 액체분율을 나타낸 것이다. Fig. 2(a)에서 보는 것과 같이 사각 공간 내부에 있는 액체상태의 PCM은 좌측 변의 낮은 온도에 의해 온도 구배가 발생하며 자연대류의 영향으로 하단 쪽 온도가
더 빠르게 좌측 변의 온도에 수렴하는 것을 확인할 수 있다. 이와 같은 현상은 Fig. 2(b)의 액체분율에서 더 뚜렷이 확인할 있다. 좌측 변의 온도가 사각 공간에 채워진 PCM의 상변화 온도인 78℃보다 낮은 조건이기 때문에 좌측 변에 가까이
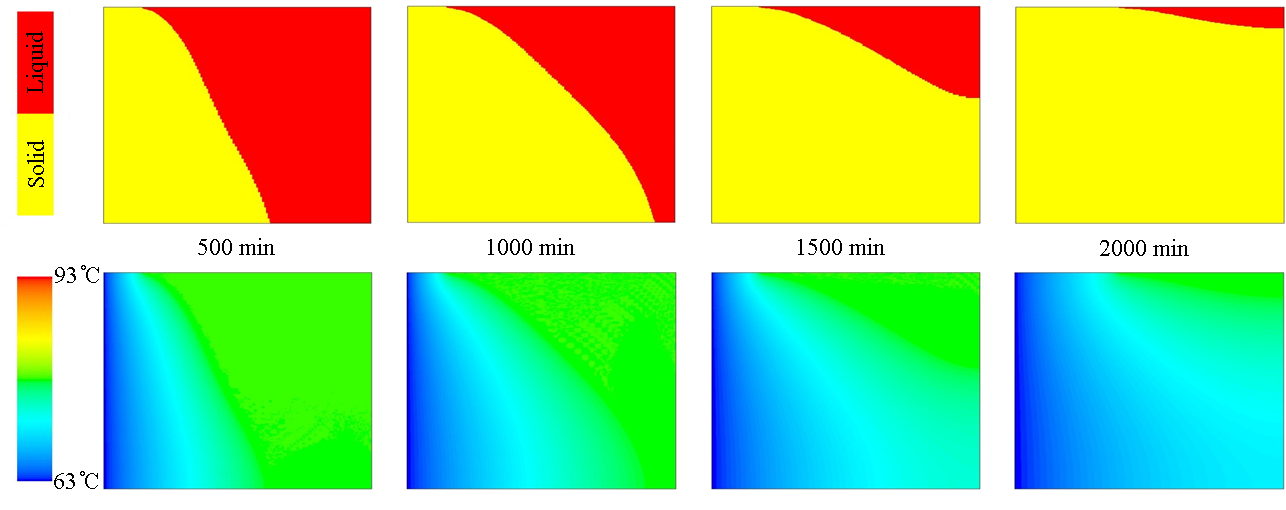
위치한 PCM 영역은 고체로 상변화 하였고 이 때 자연대류의 영향으로 상단보다 하단 쪽이 더 많이 고체로 상변화 하였다. 이와 같은 현상은 Fig. 3에서 보는 것과 같이 자연대류의 영향으로 해석 시간이 증가함에 따라 상대적으로 상단부 보다는 하단부에서 고체 영역이 더욱 확장되는 것을 확인할 수
있다. 이는 해석 시간에 따른 온도 분포에서도 동일하게 확인할 수 있다.
Fig. 2. The liquid fraction and temp. distribution of PCM on simultaneous charging and discharging condition(the elapse 1 hour after analysis start).
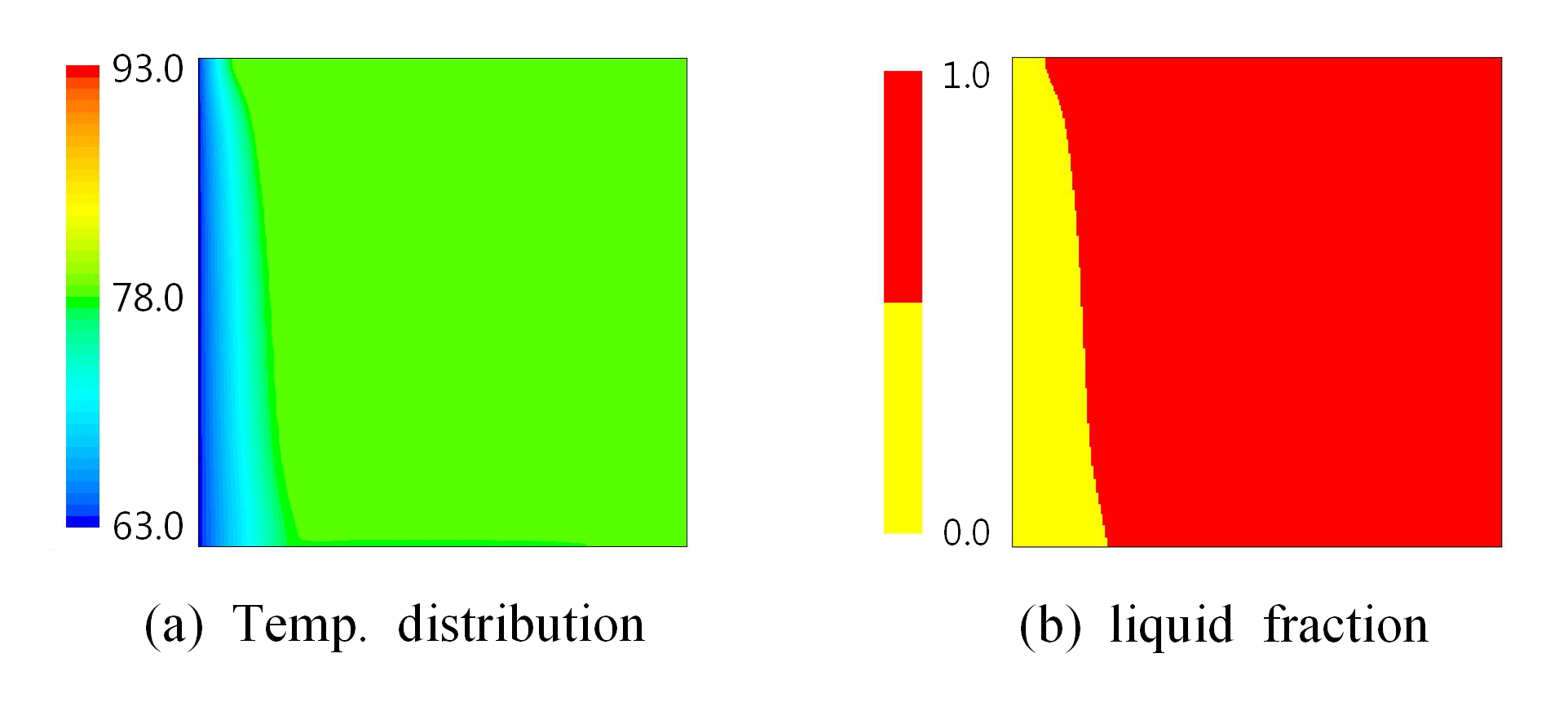
Fig. 3. The liquid fraction and temperature distribution of PCM layer during analysis process according to elapsed time(at the test No. 1).
3.2 동시 냉각/가열 조건
사각 공간의 좌우 경계면에 각각 일정온도 조건을 주었을 때 사각 공간 내부에 있는 액체상태 PCM의 액체분율과 stream line을 분석하였다.
여기서 stream line 분석을 통해 사각 공간에서 발생하는 자연대류의 영향을 확인할 수 있다. 또한 좌우 경계면의 온도조건에 의해서 사각 공간
내부의 액체상태 PCM은 가열과 냉각 조건을 동시에 적용받게 된다. 즉 사각 공간의 좌측 경계면에는 액체 상태의 PCM보다 낮은 온도를 갖도록 설정함으로써
사각 공간 내부에서 열에너지를 방출할 수 있도록 하였으며, 반대로 우측경계면은 액체 상태의 PCM보다 온도를 높게 설정하여 사각 공간 내부로 열에너지를
공급하는 조건을 갖도록 하였다.
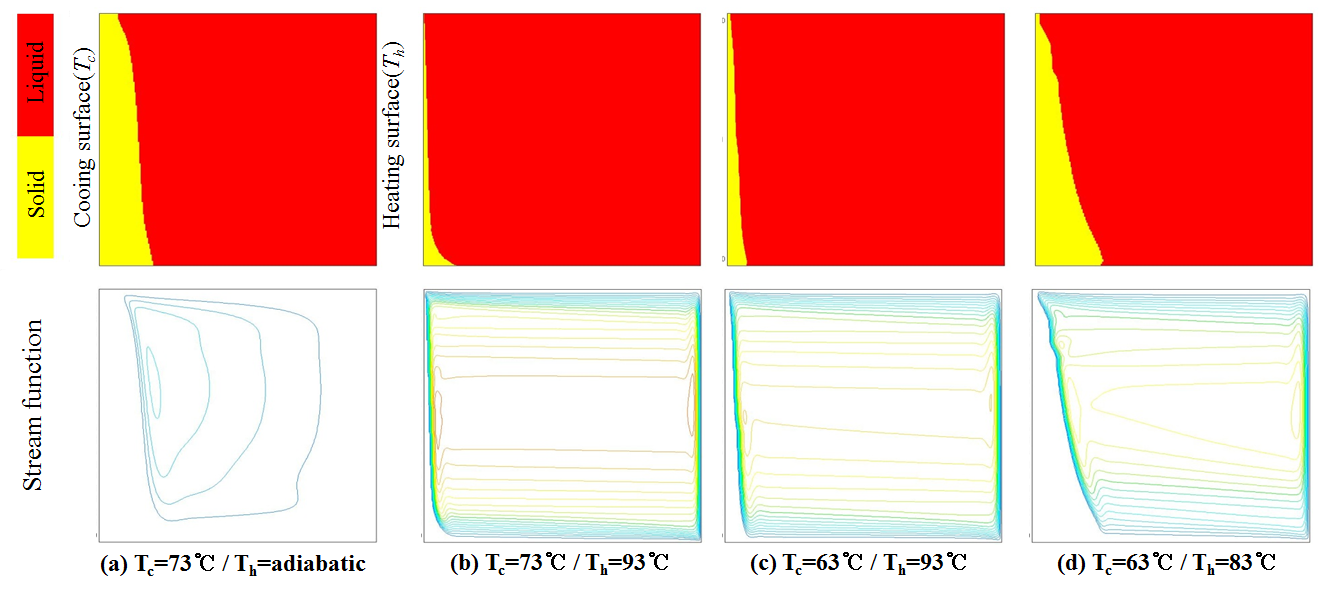
Fig. 4는 각 실험조건에서 열전달 시작 1시간 경과 후의 사각 공간 내부의 액체 분율과 stream line 분포를 나타낸 것이다. Fig. 4(b)와 Fig. 4(c)에서 보는 것과 같이 우측 경계면의 온도 Th = 93℃인 경우가 단열 및 Th = 83℃인 조건 보다 좌측 경계면에 고체 상태의 PCM이 적게 형성
되었다. 또한 동시 가열/냉각 조건이 단일 냉각 조건에서 보다 고체-액체 경계선 근처에서 자연대류가 활발하였으며 고체-액체 경계선의 기울기가 더욱
가파르게 형성되었다.
Fig. 4. The liquid fraction and stream function of PCM layer at the each analysis condition(the elapse 1 hour after analysis start).
4. 고 찰
일반적으로 PCM의 잠열을 이용하여 열에너지를 저장한 후 사용하는 열원기기는 효율적인 축/방열 조건을 가지고 있어야 한다. 하지만 대부분의 연구(9)에서 밝혀진 것과 같이 동일 전열면적에서 PCM에 열을 저장하는 과정과 열을 방출하는 과정 사이에는 시간적인 편차가 심하게 발생한다. 이는 PCM이
액체 상태와 고체 상태에서 서로 다른 열물성(Cp, k) 갖기 때문이다. 본 논문에서 사용된 PCM은 액체 상태일 때보다 고체상태에서 열전도도가 높고
비열이 낮은 특성을 가지고 있다. 이와 같은 영향으로, 동시 냉각/가열 조건에서 해석한 결과처럼 냉각면에 형성된 두꺼운 고체 영역은 열을 방출하는
과정에서 열저항으로 작용할 수 있다. 따라서 동시 가열/냉각 조건에서 적절한 가열온도와 냉각온도를 설정함에 따라 냉각면에 형성되는 고체 영역의 두께를
조절할 경우 열을 방출하는 효율을 증가 시킬 수 있다고 판단된다.
5. 결 론
액체 상태의 PCM이 충전된 사각 공간에서 좌․우 경계면에 단열 및 가열, 냉각 조건을 부여함에 따라 PCM의 상변화 현상을 해석한 결과 다음과
같음 결과를 얻었다.
(1) Mesh size에 따라 응고완료 시간과 계산 정확도에 영향이 있음을 확인하였고 해석 시 모델에 따른 적정 Mesh size에 대하여 고려할
필요가 있다.
(2) Fluent 해석 과정에 자연대류를 고려하였으며, 이로 인한 영향으로 액체 상태의 PCM이 고체로 상변화하는 과정에서 고체-액체 경계면이
구배를 형성하였다.
(3) 동시 냉각/가열 조건에서 가열면의 조건에 따라 고체-액체 경계면이 형성되는 구배가 영향을 받으며 동일 시간에서 가열면 온도가 높을수록 냉각면에
형성되는 고체 영역이 감소하였다.
후 기
본 연구는 산업통상자원부 제조기반 산업핵심기술개발사업(생산시스템)의 연구비 지원에 의해 수행되었습니다(과제번호 : 10049090).
References
Dutil Y., Rousse D. R., Salah N. B., Lassue S., Zalewskic L., 2011, A review on phase-change
materials : Mathematical modeling and simulations, The Journal of Renewable and Sustainable
Energy Reviews, Vol. 15, No. 1, pp. 112-130

Brent A. D., Voller V. R., Reid K. J., 1988, Enthalpy Porosity Technique for Modeling
Convection Diffusion Phase Change Application to the melting of a Pure Metal, The
Journal of Numerical Heat Transfer, Vol. 13, No. 3, pp. 297-318

Viswanath R., Jaluria Y., 1993, A comparison of different solution methodologies for
melting and solidification problems in enclosures, Numer Heat Transfer, Part B : Fundam,
Vol. 24, No. 1, pp. 77-105

Shamsundar N., Srinivasan R., 1978, Analysis of energy storage by phase change with
an array of cylindrical tubes, In : Thermal storage and heat transfer in solar energy
systems, pp. 35-40

Roy S. K., Sengupta S., 1989, Melting of a free solid in a spherical enclosure : effects
of subcooling, J Solar Energy Eng, Vol. 111, No. 1, pp. 32-36

Trp A., 2005, An experimental and numerical investigation of heat transfer during
technical grade paraffin melting and solidification in a shell-and-tube latent thermal
energy storage unit, Solar Energy, Vol. 79, No. 6, pp. 648-660

Zhang Y., Su Y., Zhu Y., Hu X., 2001, A General model for analyzing the thermal performance
of the heat charging and discharging process of latent heat thermal energy storage
systems, Trans ASME, J Sol Energy Eng, Vol. 123, No. 3, pp. 232-236

Velraj R., Seeniraj R. V., Hafner B., Faber C., Schwarzer K., 1997, Experimental analysis
and numerical modelling of inward solidification on a finned vertical tube for a latent
heat storage unit, Solar Energy, Vol. 60, No. 5, pp. 281-290

Kim H. K., Lee D., Peck J. H., Kang D., 2013, Numerical Study of Heat Transfer with
Selective Phase Change in Two Different Phase Change Materials, Korean Journal of
Air-Conditioning and Refrigeration Engineering, Vol. 29, No. 9, pp. 477-483
