Changjun Oh
(오창준)
1
Yongtaek Lee
(이용택)
2†
-
Department of Unmanned System Engineering, Graduate School of Hannam University, Daejeon,
34430, Korea
(한남대학교 대학원 무인시스템학과)
-
Department of Mechanical Engineering, Hannam University, Daejeon, 34430, Korea
(한남대학교 기계공학과)
Copyright © 2016, Society of Air-Conditioning and Refrigeration Engineers of Korea
keywords
PEMFC, Gas diffusion layer, Gas permeability, Compression
키워드
고분자 전해질 연료전지, 가스확산층, 기체투과율, 압축
기호설명
A:시편 면적 [m2]
CR:압축비
dg:공극 직경 [m2]
k:기체투과율 [m2]
r:시편 반지름 [m]
Q:유량 [L/min]
h:시편 두께 [m]
h0:비압축상태 시편 두께 [m]
P:압력 [Pa]
x:기체 이동 거리 [m]
그리스 문자
μ:점도 [Pa·s]
ε:공극률
ε0:비압축상태 공극률
1. 서론
1.1 연구 배경
고분자 전해질 연료전지(proton exchange membrane fuel cell, PEMFC)는 연료로 공급되는 수소와 공기 중의 산소가 전해질막(membrane)을
사이에 두고 공급되어 전해질막의 표면의 촉매층에서 화학반응을 일으키며 그 과정에서 수소에서 분리된 전자의 이동으로 인하여 전력을 생산한다. 이러한
화학반응의 정도는 연료전지의 성능에 직접적인 영향을 미치며 따라서 공급되는 수소와 산소를 촉매층으로 원활하고 고르게 이동시키는 가스확산층(gas diffusion
layer, GDL)의 역할이 매우 중요하다. 반응가스의 촉매층으로의 확산 이외에도 GDL은 촉매층에서 생성되는 물을 채널쪽으로 배출시키는 통로의
역할도 하며 전류와 열의 전도체의 역할을 수행한다. 뿐만 아니라 기계적으로 약한 강도를 가지는 전해질막이 분리판으로부터 직접적인 손상을 입지 않도록
완충역할까지 수행한다.
이러한 GDL의 표면은 Fig. 1에 제시된 바와 같이 탄소섬유가 무작위로 얽혀있는 형태를 가지며 이러한 형태가 여러층 겹쳐져서 GDL을 구성하게 된다. Fig. 1의 (a)-(b)는 GDL의 표면 발수성을 증가시키기 위하여 첨가되는 polytetrafluoroethylene(PTFE)의 질량비로 구분된다. Fig. 2에는 GDL의 단면을 나타내었으며 그 형태에서 알 수 있듯이 평면과 단면의 구조가 상이하여 기체의 흐름에 있어서 다른 특성을 야기한다. In-plane
흐름은 주로 확산현상에 기인하여 발생하는 반면 through-plane 흐름은 대류현상에 지배를 받는다.(2)
Fig. 1. SEM images of TGPH-060 with (a) 0 wt.% PTFE and (b) 20 wt.% PTFE loading. These have same pore structure with TGPH-120.(1)

Fig. 2. SEM image of the cross section of TGPH-060 with 0 wt.% of PTFE loading.

PEMFC의 전체 혹은 일부영역에서의 물질전달의 모델링을 위해서는 PEMFC를 구성하는 전해질막, 촉매층, GDL, 그리고 채널내의 유동을 별도로
해석해야 하며 GDL에서의 물질전달은 공극을 구성하는 탄소섬유의 구조의 형태가 명확히 제시되어 있지 않으며 마이크로 단위의 흐름이기 때문에 이론적인
해석이 거의 불가능하다. 따라서 현재까지는 모델링 대상이 되는 GDL의 실험적 연구로 얻어진 공극률, 기체투과율, 전기전도율, 열전도율 등의 값이
모델링에 사용되고 있다.(3, 4) 기존의 문헌에서 제공되는 가스확산층의 물성치들은 대부분 GDL에 외력이 가해지지 않았거나 혹은 일정한 하중이 가해진 상태에서 측정되었다.(5) 따라서 Zhou et al.(6)의 연구와 같은 모델링 연구에서는 GDL의 압축에 의한 투과율의 변화를 기존에 제시된 이론 식을 이용하여 예측 적용하였고, Ahmed et al.(7)은 채널과 채널 사이의 압축되는 부분의 기체투과율을 압축되지 않은 부분보다 임의로 작게 설정하여 모델링 연구를 수행하였다.
일부 실험적 연구에서는 압축상태의 GDL에 대한 기체투과율을 제시하기도 하였으나 압축하중과 변형률에 대한 정보는 제시되지 않았으며, 본 연구의 특징인
PTFE 함유량에 대한 특성이 제시되지 않았다.(8)
본 연구에서는 다양한 PTFE 함량을 갖는 GDL의 압축하중과 변형률을 정밀하게 측정하며 각 압축단계에서의 in-plane 기체투과율을 실험적으로
측정하고 그 결과를 제시하고자 한다. 이를 통하여 PTFE의 함량이 GDL의 기계적인 특성에 미치는 영향을 유추하고 기체투과율의 변화와의 연관성을
도출하여 향후 GDL의 기체투과율 물성치가 필요한 연구의 기초데이터로 활용될 수 있도록 하고자 한다.
1.2 관련 이론
다공성물질에서의 기체투과율은 다공성물질을 통과하는 유체의 유량과 미세한 공극을 통과하면서 발생하는 압력차이에 의하여 아래의 Darcy’s law에
의하여 결정된다.
본 실험에서는 Fig. 3과 같은 원판형태의 시편을 이용하여 평면 기체투과율을 측정하였으며 원판형태의 시편의 고리모양 미소 체적에 대하여 식(1)을 적용하면
Fig. 3. Derivation of modified Darcy’s law for a disk.
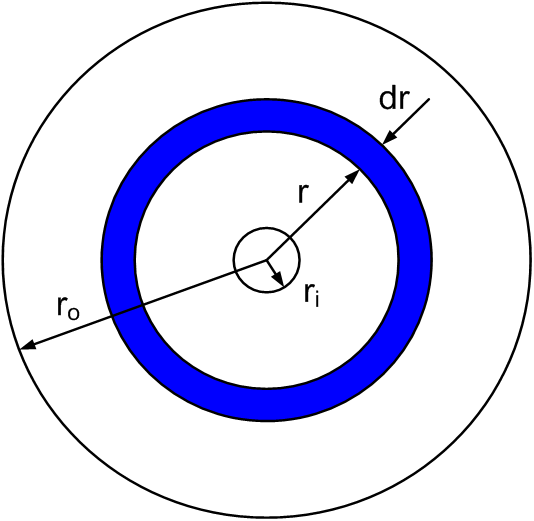
여기서 r과 P의 증가방향이 서로 다르므로 음의 부호가 고려되었다. r = ri로부터 r = ro까지 적분하면
본 실험에서 사용된 원판형태의 시편에서의 기체투과율은 측정된 압력차이와 유량데이터를 이용하여 식(5)로부터 계산되었다.
다공성물질의 변형에 의한 공극률의 변화는 Wang and Chen(9)에 의하여 압축비(compression ratio, CR)에 관한 식으로 식(6)과 같이 제시되었다.
그리고 그로 인한 기체투과율의 변화는 Blake-Kozeny 식을 이용하여 식(7)과 같이 표현된다.
여기서 dg는 공극의 직경이며 일반적으로 20 μm 정도로 알려져 있다.
또한, Chang et al.(10)은 제조사와 PTFE 함량을 밝히지 않은 두께 120 μm의 GDL에 대해서 기체투과율을 측정하고 Carmen-Kozeny 식(8)을 이용하여 공극률의 변화를 예측하였다.
여기서 Ka는 Kozeny 상수이며 60에서 180사이의 값을 가진다. 이 결과를 통하여 압축된 상태의GDL의 두께와 공극률의 관계를 식(9)와 같이 제시하였다.
위에 제시된 변형률과 기체투과율과의 관계는 다공성물질의 구조적 특성이 고려되지 못한 단점이 있다. Fig. 1과 Fig. 2에서 드러나듯이 GDL은 이방성을 띠며 기체투과율 역시 기체의 투과 방향에 따라서 전혀 다른 값을 나타낼 것으로 보인다. 본 연구에서는 GDL이 면에
수직하는 방향으로 압축되는 과정에서의 평면 (in-plane) 기체투과율을 측정하고 위에 제시된 결과와 비교하였다.
2. 실험장치 및 방법
2.1 실험장치
본 연구에서 사용된 실험장치는 기본적으로 유량제어부와 시편압축부로 구성되어 있다. Fig. 4는 시편압축부의 다이어그램이며 시편이 장착부의 하단에 로드셀을 장착하여 시편에 가해지는 하중을 실시간으로 측정할 수 있게 하였고 스테핑모터와 이송스크류를
이용하여 시편을 수직으로 압축할 수 있게 제작하였다. 하중에 따른 시편의 변형은 초근접카메라를 이용하여 촬영후 상·하단 프레스의 거리의 변화로 계산하였다.
스테핑모터의 회전수로부터 프레스의 직선 이송거리를 계산하여 시편의 변형률을 계산할 수 있으나 모터에 과도한 토크가 가해지면 주어진 신호와 실제 회전수의
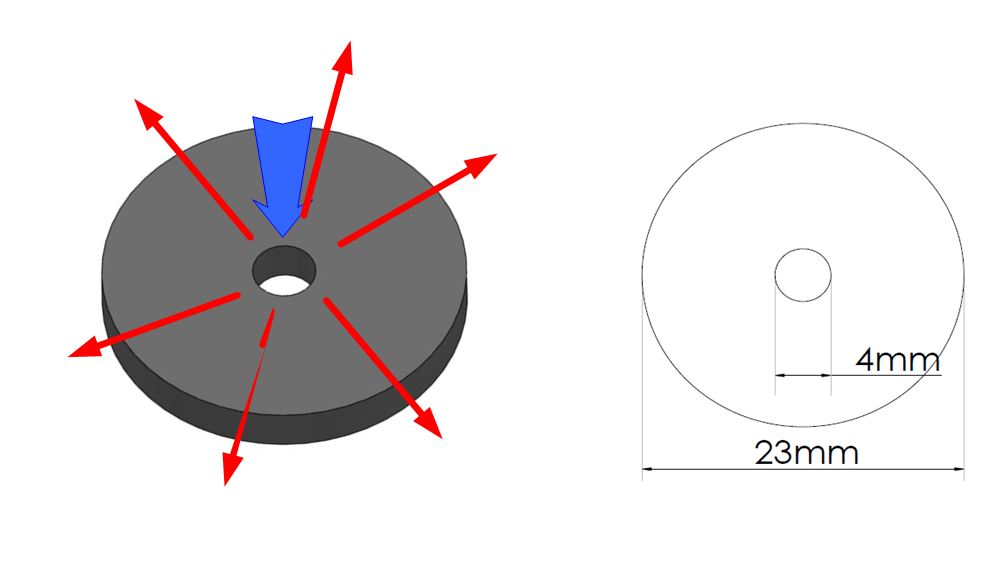
차이가 발행할 수 있으므로 카메라를 이용한 변형률 측정을 수행하였다. GDL 시편은 Fig. 5와 같이 원판형태로 제작하였으며 중심부로 기체가 유입되어 면을 따라 투과된 후 원판의 바깥 테두리로 배출되도록 장착되었다. GDL에 공급되는 공기의
유량과 압력은 유량제어부에서 측정하였다.
Fig. 4. Schematic diagram of experimental setup.
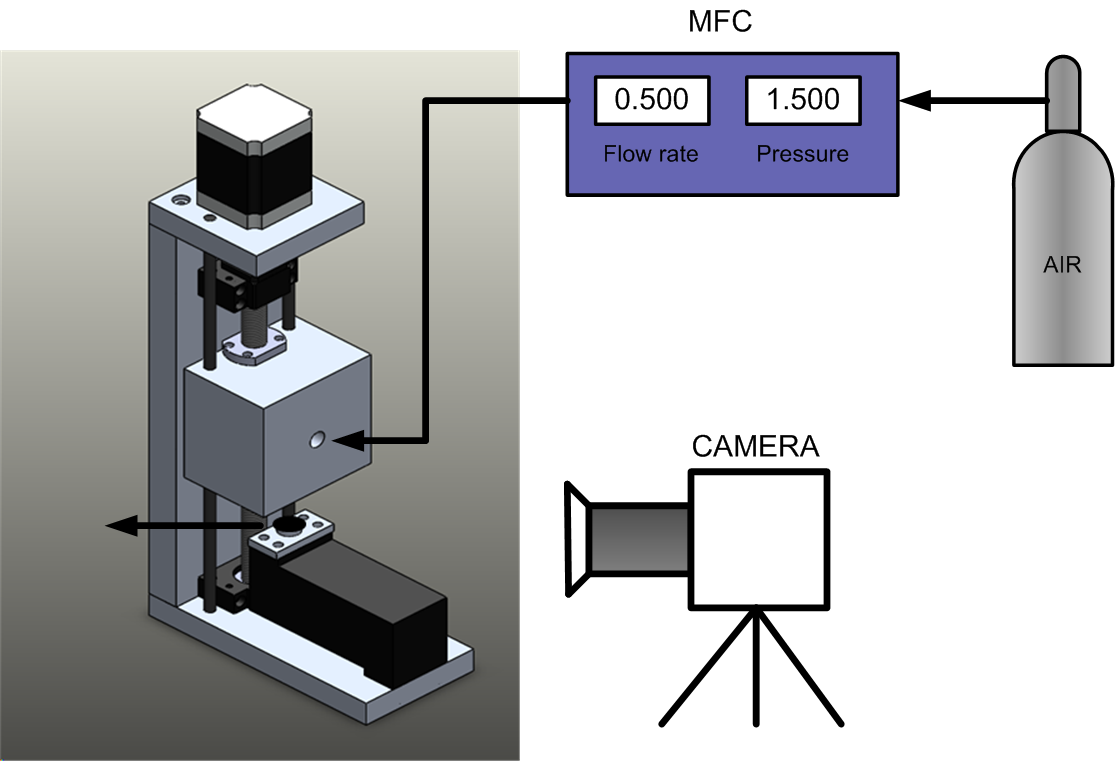
Fig. 5. Dimension of GDL specimen and the flow direction.
2.2 실험조건
PEMFC의 체결압력에 의한 성능의 변화를 측정하는 기존의 연구들에서 적용한 PEMFC 스택의 체결압력은 일반적으로 단위면적 기준으로 1,000~2,000
kN/m2 정도이다. 그러나 PEMFC 스택에는 GDL의 외부를 따라 누설을 방지하기 위하여 가스켓이 사용되며 대부분의 체결력은 가스켓에 가해져 가스켓이 어느정도
압축변형되고 난 이후에 GDL에 체결력이 전해진다. 따라서 GDL에 직접적으로 가해지는 수직하중이 어느 정도의 범위에 위치하는가에 대한 연구가 기존에
많이 수행되지 못한 상태이다. 본 연구에서는 GDL의 단위면적당 450 kN/m2까지 하중을 가하면서 압축하중에 따른 변형률을 측정하고 각각의 변형상태에서 공기의 유량을 0.5 slpm에서 4 slpm까지 공급하면서 GDL의 상단에
걸리는 압력을 측정하였다. 시편에 가해지는 하중이 0.05 kgf, 즉 단위면적당하중으로 1.2 kN/m2이 가해질 때 상단프레스가 시편과 접촉한 것으로 보고 그 때의 시편의 두께를 기준으로 변형률을 계산하였다.
본 실험에 사용된 GDL은 Toray사의 TGPH-120이며 물의 발수력을 강화하기 위하여 첨가하는 PTFE는 질량비 기준으로 0 wt.%, 5
wt.%, 10 wt.%, 그리고 30 wt.%의 4가지를 사용하였다. 각 GDL의 압축되지 않은 상태에서의 공극률을 MSP 기법(11)으로 측정한 결과를 table 1에 제시하였다. 한 장의 GDL은 두께가 약 370 μm로 매우 얇기 때문에 측정의 오차를 줄이기 위하여 5장의 GDL을 겹쳐서 하나의 시편으로 사용하였다.
Table 1. Porosity of uncompressed TGPH-120 with various PTFE loading
|
|
PTFE loading
|
|
Porosity
|
0%
|
5%
|
10%
|
30%
|
|
0.771
|
0.755
|
0.747
|
0.637
|
3. 결과 및 고찰
Fig. 6은 GDL 시편에 수직 하중을 가하면서 GDL의 압축에 의한 압축비를 나타낸다. 여기서 압축비, CR은 식(10)와 같이 정의되었다.
Fig. 6. Variation of compression ratio for the GDLs with various PTFE loading according to the compression.
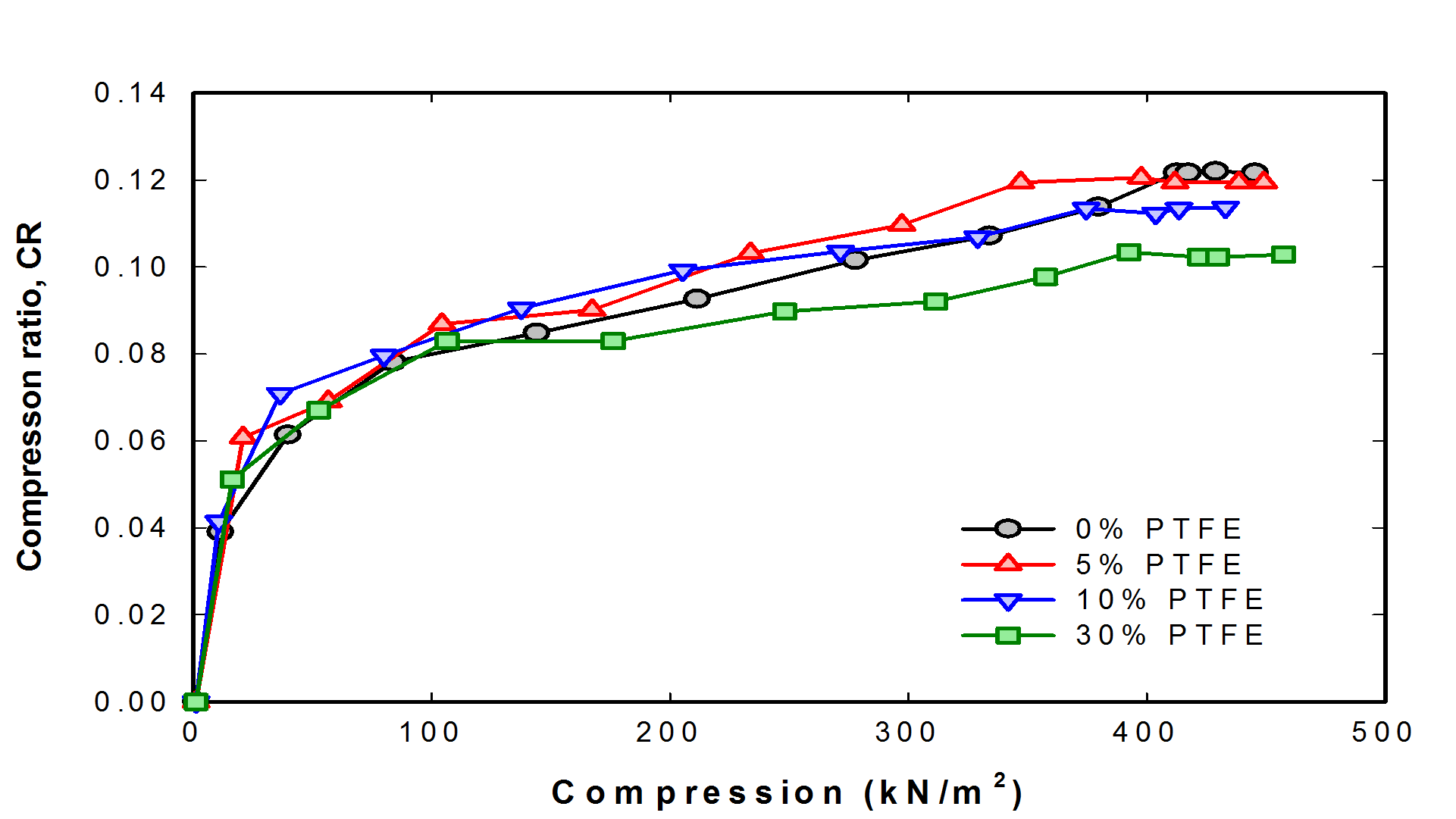
압축하중이 증가함에 따라 시편의 압축비가 점차 증가하며 압축비의 증가폭은 점차 줄어들어 압축하중이 약 350~400 kN/m2에 도달하면 압축하중이 증가하여도 압축비가 거의 일정하게 유지되기 시작한다. 이는 수직하중에 의하여 GDL을 구성하는 탄소섬유의 층과 층사이의 공극이
점차 줄어들기 시작하여 약 350 kN/m2 정도의 하중에서 탄소섬유끼리의 접촉으로 인하여 섬유질의 파손이 있지 않는 한 더 이상의 변형이 발생하지 않게 됨을 의미한다. 이 결과는 하중과 변형률을
다른 실험장치로 측정하였던 기존의 연구(12)와 다소 차이가 존재하는데 스테핑모터의 회전수를 직선방향의 거리로 단순 환산하였던 기존 연구 방법에서 높은 압축하중범위에 오차가 다소 있었음을 확인할
수 있다.
PTFE의 함유량에 따라서 압축비의 변화폭이 다소 다르게 나타나는데 PTFE가 30 wt.% 함유된 GDL은 압축비의 증가가 다른 GDL에 비하여
다소 적으며 이는 주로 탄소섬유의 접합부에 도포되는 PTFE가 구조의 변형에 있어서 저항 역할을 했기 때문인 것으로 판단된다. 다만 0~10 wt.%
PTFE들에 있어서는 특정한 경향성을 찾기 어려운데 도포된 PTFE의 양이 적어서 PTFE의 양에 의한 압축비의 차이보다 GDL 층을 구성하는 탄소섬유의
구조가 압축비에 더 큰 영향을 미치는 것으로 해석된다.
압축되지 않은 자연상태의 GDL에 대한 공극률의 측정은 거의 모든 표면에 젖음성(wettability)이 매우 낮은 수은을 높은 압력으로 강제 주입하는
MIP(mercury intrusion porosimetry) 방법(1) 과 이와 반대로 거의 모든 표면에 젖음성이 매우 좋은 옥탄과 같은 액체의 자발적인 함침(impregnation)을 이용한 MSP(method of
standard porosimetry) 방법(11) 등을 사용하면 공극크기분포(pore size distribution)와 함께 측정할 수 있다. 그러나 압축변형된 상태의 GDL에 대한 공극률의
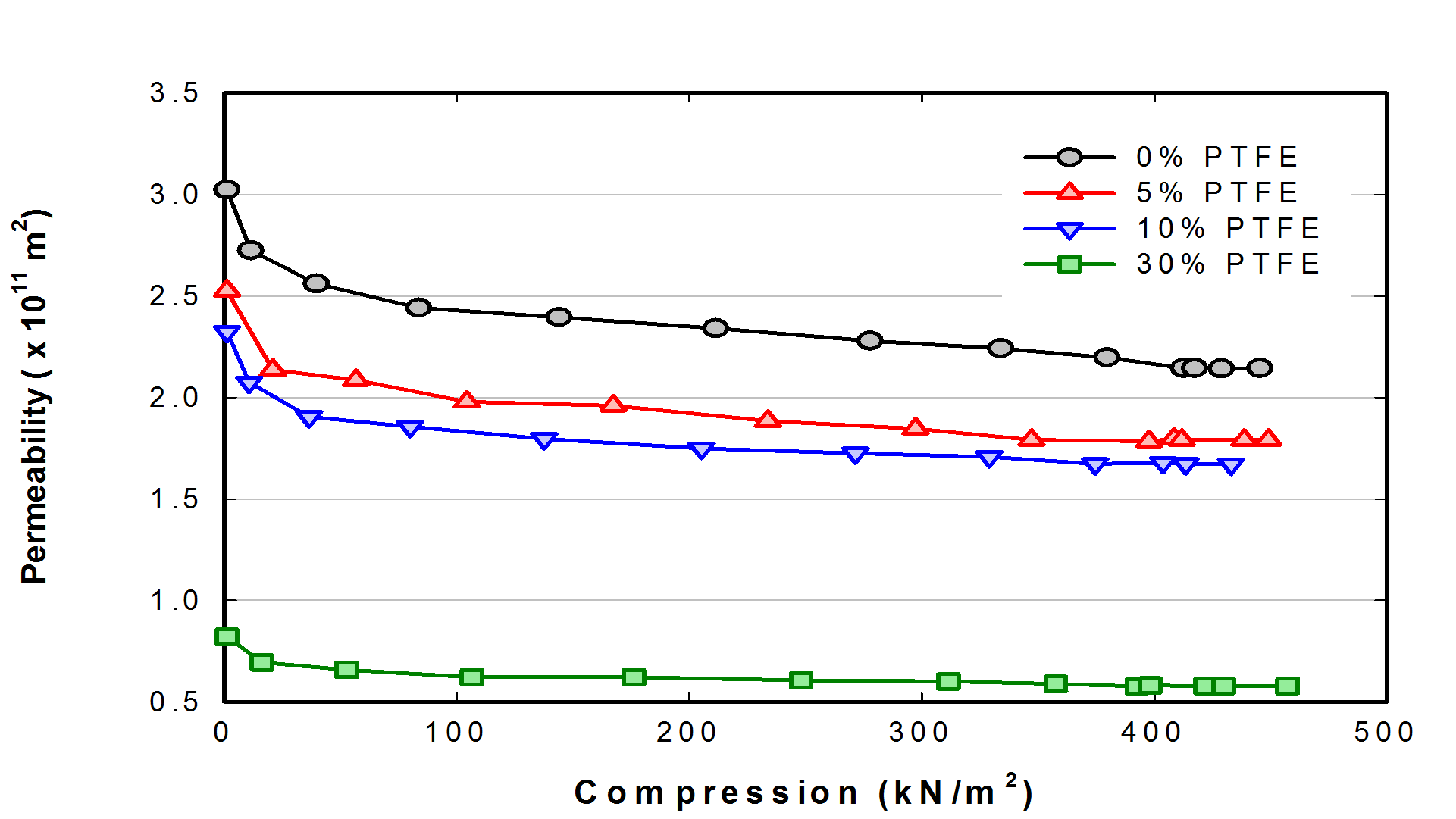
변화를 실험적으로 측정한 기존 연구는 찾아볼 수 없으며 다만 Wang and Chen(9) 이 제시한 식(6)을 이용하여 두께의 변화만으로 공극률을 예측할 수 있다. 또한 이와 같이 계산된 공극률의 변화와 Blake-Kozeny 식(7)을 이용하여 기체투과율의 변화역시 예측할 수 있다. 계산된 공극률과 기체투과율의 변화를 Fig. 7과 Fig. 8에 나타내었다.
Fig. 7. Variation of porosity of TGPH-120 according to the compression which is determined by Eq. 6.
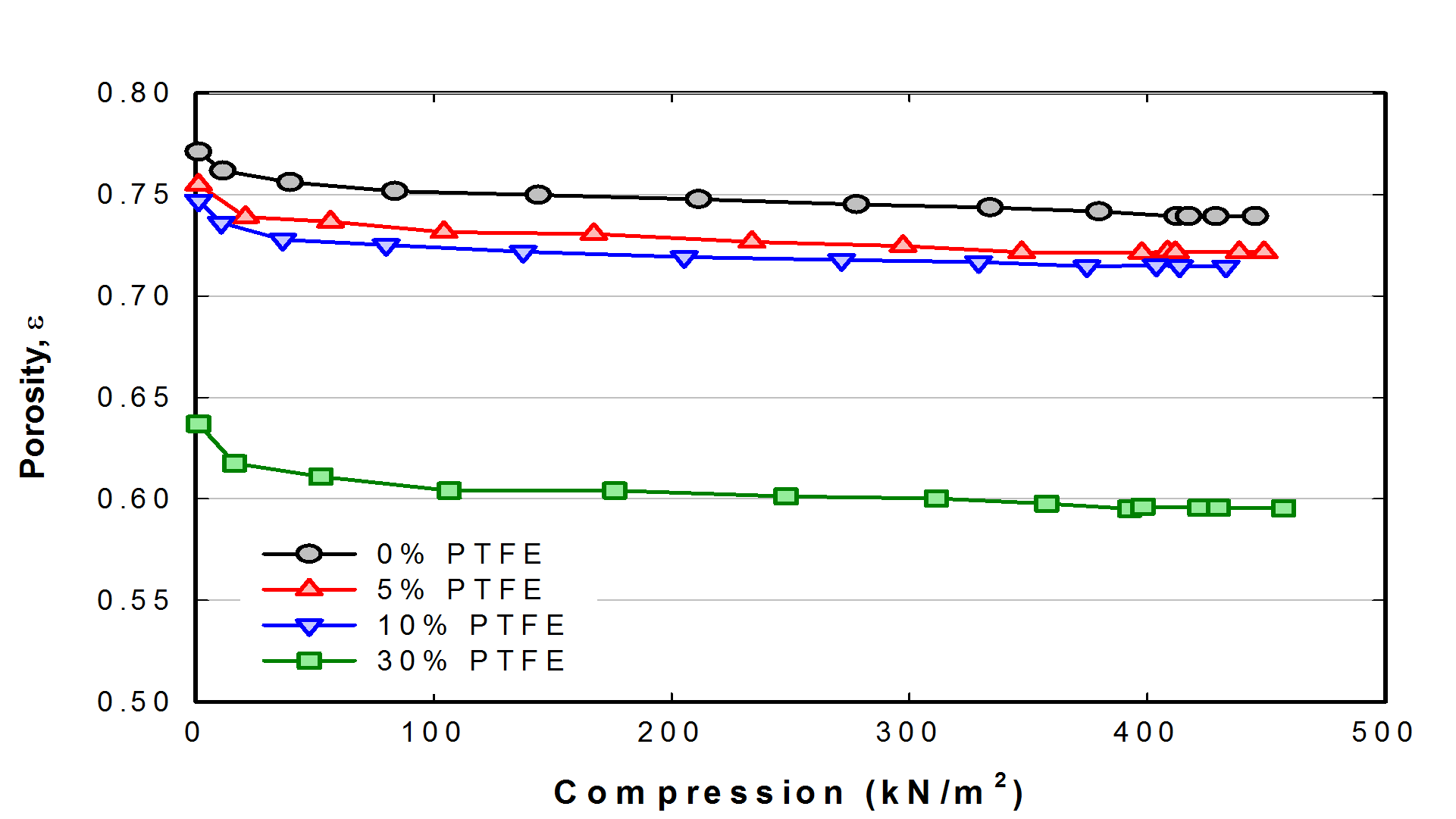
Fig. 8. Estimated in-plane permeability of TGPH-120 according to the compression which is determined by Eq. 7.
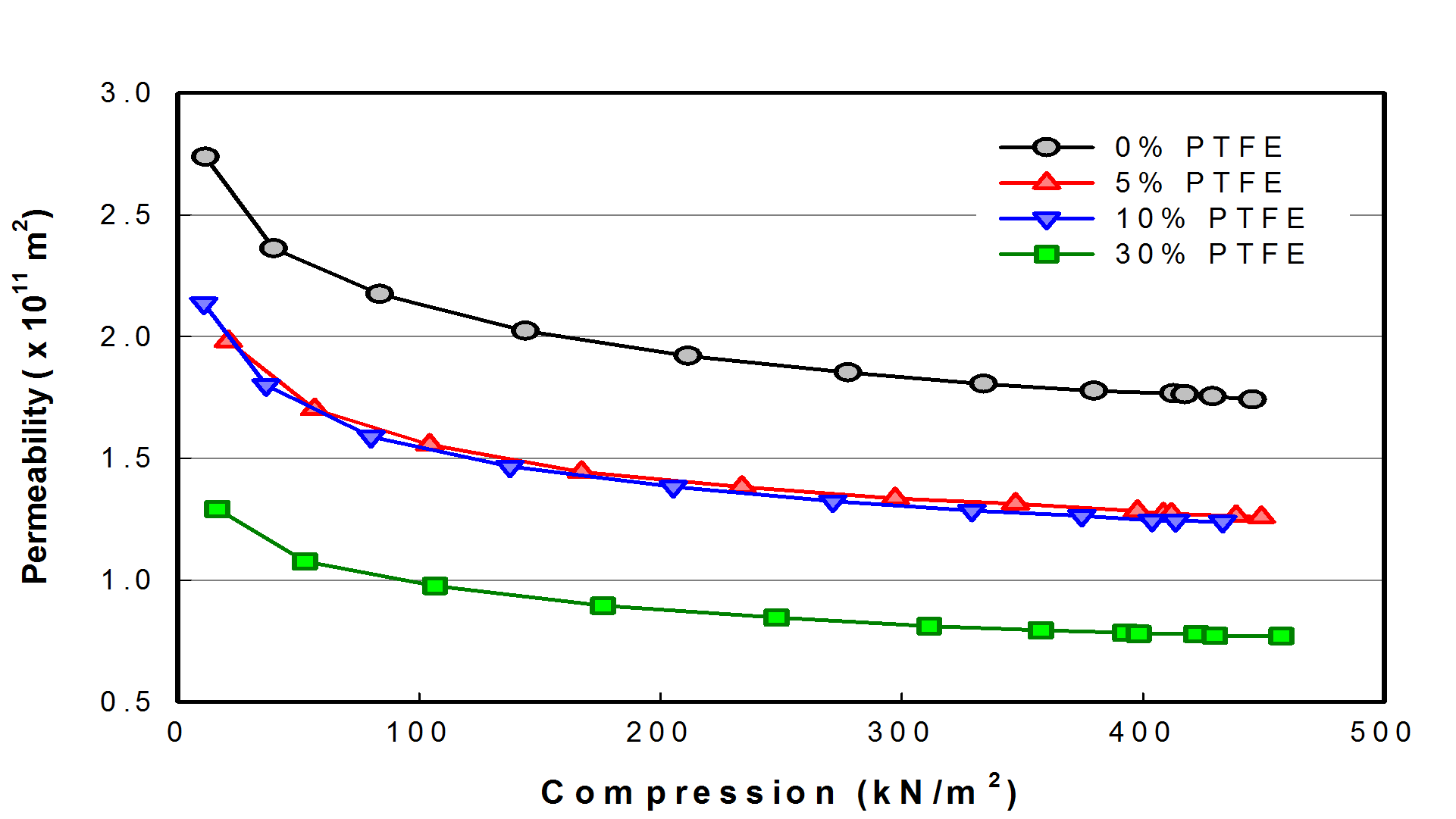
본 연구에서 GDL의 각 압축변형 상태에서 측정한 유량과 압력강하의 관계는 Fig. 9에 제시된 바와 같다. Fig. 9에는 대표적으로 0 wt.%의 PTFE가 함유된 GDL의 결과를 나타내었으며, PTFE의 함유량이 다른 GDL에서도 Fig. 9와 같이 유량에 따라 직선형태의 압력강하를 나타내었다. 각 압축하중에 대하여 유량과 압력강하의 관계를 선형회귀를 통하여 Q/(Pi-Po)를 구하고 이를 식(5)에 적용하여 기체투과율을 계산하여 Fig. 10에 제시하였다. 결과적으로 PTFE가 함유되지 않은 TGPH-120의 in-plane 기체투과율은 압축이 되지 않았을 때 약 2.74×10-11 m2에서 400 kN/m2 이상으로 압축되면 1.75×10-11 m2로 36% 감소되며 30 wt.%의 PTFE를 함유하고 있는 TGPH-120은 동일한 조건에서 1.29×10-11 m2에서 0.77×10-11 m2로 40% 정도 감소하였다. PTFE의 함유량이 5 wt.%와 10 wt.%인 GDL은 측정된 기체 투과율이 큰 차이를 보이지 않고 있으며 다만 10
wt.% PTFE에서 소폭 감소된 기체투과율을 나타내었다. 실험에 의하여 측정된 결과는 앞서서 Blake-Kozeny 식에 의하여 예측된 수치와 유사한
범위를 나타내며 30 wt.% PTFE의 TGPH-120의 결과는 Feset et al.(8)이 제시한 TGPH-060의 결과와 유사하다.
Fig. 9. Variation of pressure drop according to flow rate for the in-plane diffusion of 0 wt.% PTFE treated TGPH-120.
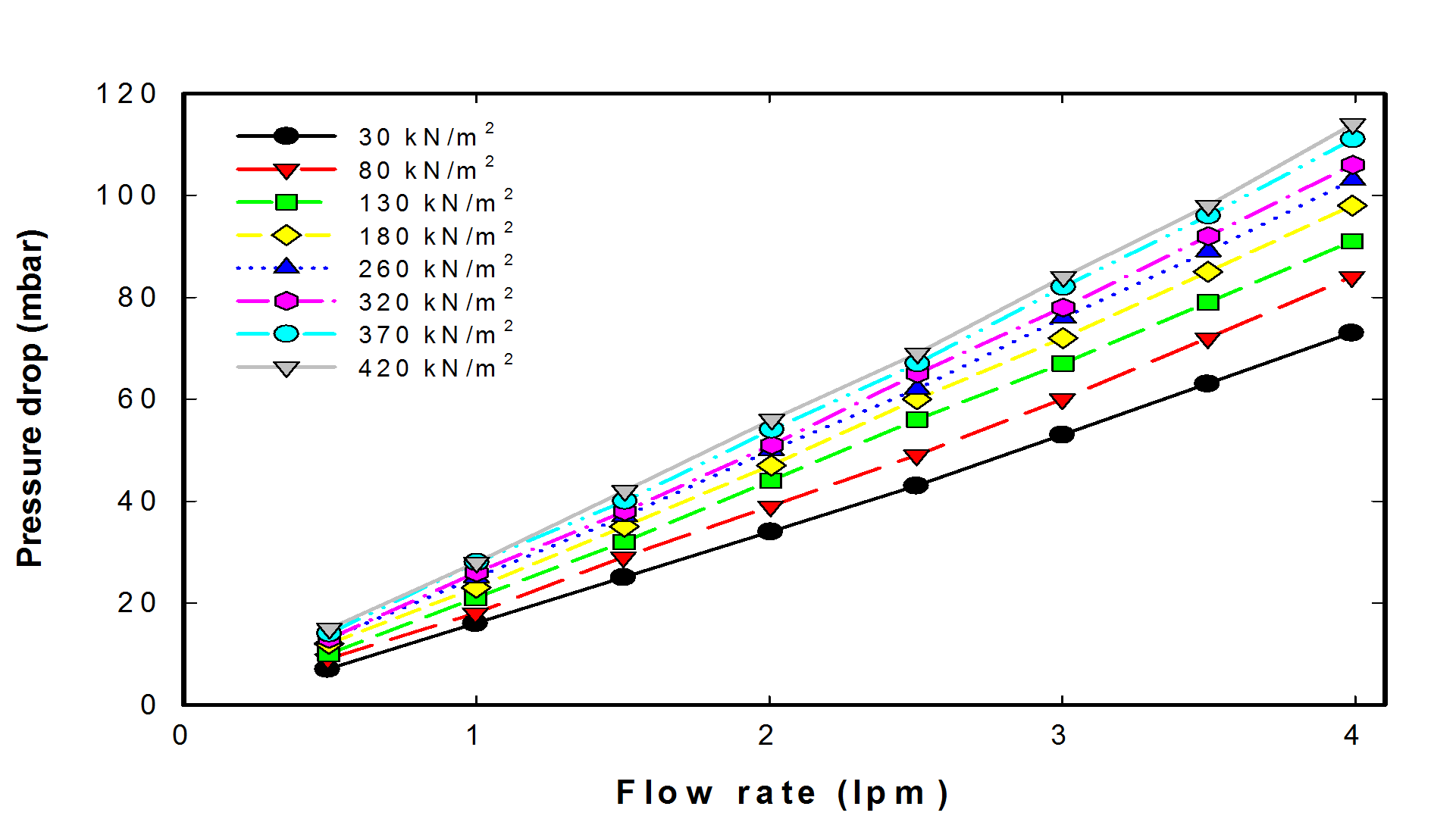
Fig. 10. In-plane permeability of TGPH-120 according to the compression which is determined by experiment.
4. 결 론
PEMFC에서 채널을 통해 공급되는 반응가스를 전해질막 표면의 촉매층으로 확산시키며 촉매층에서 생성되는 물을 채널방향으로 이동시키는 역할을 하는
다공성물질인 가스확산층 (GDL)은 스택의 체결압력에 의하여 압축변형된 상태로 존재하게 되나 비압축상태의 기체투과율에 정보만 널리 알려져 있고, 압축변형된
상태의 기체투과율에 대한 정보는 부족하다. 특히 GDL에는 발수성을 높이기 위하여 PTFE를 다양한 질량비로 주입하게 되며 이러한 PTFE의 질량비에
따라서 압축에 따른 변형률 특성 및 기체투과율을 실험적으로 측정하여 제시하였다.
(1) 0~30 wt.% PTFE의 GDL을 450 kN/m2까지 압축하였을 때 약 400 kN/m2 이후에서는 변형률의 변화가 거의 없으며 각 GDL의 변형률은 10%(30 wt.% PTFE)에서 12%(0 wt.% PTFE)까지 나타났다.
(2) GDL의 기체투과율은 압축이 진행됨에 따라 로그형태로 감소하며 400 kN/m2로 압축변형된 후에는 PTFE의 함유량이 0, 5, 10, 30 wt.%로 증가함에 따라 각각 1.75×10-11m2, 1.28×10-11m2, 1.24×10-11m2, 0.77×10-11m2의 값을 나타내었다.
후 기
이 논문은 2015학년도 한남대학교 학술연구조성비에 의하여 연구되었으며 이에 감사드립니다.
References
Lee Y., Kim B., Kim Y., Li X., 년도, Degradation of gas diffusion layers through repetitive
freezing, Applied Energy, Vol. 88, No. 12, pp. 5111-5119

Tamayol A., Bahrami M., 2010, In-plane gas permeability of proton exchange membrane
fuel cell gas diffusion layers, FEDSM2010-ICNMM2010, pp. 1-8

Hwang J. J., 2007, A complete two-phase model of a porous cathode of a PEM fuel cell,
J. Power Sources, Vol. 164, No. 1, pp. 174-181

Jiang F., Wang C. Y., 2014, Numerical modeling of liquid water motion in a polymer
electrolyte fuel cell, Int. J. Hydrogen Energy, Vol. 39, No. 2, pp. 942-950

Gostick J. T., Fowler M. W., Pritzker M. D., Ioannidis M. A., Behra L. M., 2006, In-plane
and through-plane gas permeability of carbon fiber electrode backing layers, J. Power
Sources, Vol. 162, No. 1, pp. 228-238

Zhou P., Wu C. W., Ma G. J., 2007, Influence of clamping force on the performance
of PEMFCs, J. Power Sources, Vol. 163, No. 2, pp. 874-881

Ahmed D. H., Sung H. J., Bae J., 2008, Effect of GDL permeability on water and thermal
management in PEFMCs-I. Isotropic and Anisotropic permeability, Int. J. Hydrogen Energy,
Vol. 33, No. 14, pp. 3767-3785

Feser J. P., Prasad A. K., Advani S. G., 2006, Experimental characteristics of in-plane
permeability of gas diffusion layers, J. Power Sources, Vol. 162, No. 2, pp. 1226-1231

Wang Y., Chen K. S., 2011, Effect of spatially-varying GDL properties and land compression
on water distribution in PEM fuel cells, J. Electrochem. Soc., Vol. 158, No. 11, pp.
B1292-B1299

Chang W. R., Hwang J. J., Weng F. B., Chan S. H., 2007, Effect of clamping pressure
on the performance of a PEM fuel cell, J. Power Sources, Vol. 166, No. 1, pp. 149-154

Lee Y., 2013, Porometric study on the gas diffusion layer in PEMFCs using method of
standard porosimetry, Korean J. Air-Conditioning and Ref. Eng., Vol. 25, No. 2, pp.
064-069

Lee Y., 2013, Variation of porosity and gas permeability of gas diffusion layers under
compression, Trans. Korean Soc. Mech. Eng. B, Vol. 37, No. 8, pp. 767-773
