Seo Jeong-Ah
(서정아)
1
Shin Younggy
(신영기)
1†
Lee Kyoung-ho
(이경호)
2
-
Department of Mechanical Engineering, Graduate School Sejong University, Seoul, 05006,
Korea
(세종대학교 기계공학과)
-
Solar Thermal Laboratory, Korea Institute of Energy Research, Taejeon, 34101, Korea
(한국에너지기술연구원)
Copyright © 2016, Society of Air-Conditioning and Refrigeration Engineers of Korea
keywords
Renewable energy, Optimization, Quadratic programming, PV arrays, Model predictive control
키워드
신재생에너지, 최적화, 이차계획법, 태양광 전지, 모델 예측 제어
기호설명
A:matrix
C:배터리 충전량 [J], 열용량 [J/℃]
c:전력요금제 [won/kWh]
Ch:충전 전력 [W]
D:수요 전력(= Phome + Pac) [W]
Dch:방전 전력 [W]
DOD:Depth of discharge
e:온도오차 [℃]
EPS:과잉공급전력 [W]
K:목적함수 계수 행렬
k:현재 시점 [hr]
lb:lower bound
NB:배터리 수
P:electric power [W]
Q:heat [W]
RCB:Battery rated capacity [W]
T:temperature [℃]
x:의사결정 변수
ub:upper bound
:시간 간격 [sec]
그리스 문자
:Discharge efficiency of battery [%]
:Hourly self-discharge of battery [%/hr]
하첨자
a:ambient
ac:air conditioning
B:battery
eq:등식
grid:main grid
home:home use except for heating and cooling
i:inside home
max:최대
o:outside
PV:photovoltaic
s:solar
set:설정
w:거실을 둘러싼 벽체
z:거실 구역 내 공기와 인테리어
1. 서론
지방자치단체들은 ‘신에너지 및 재생에너지 개발 이용 보급 촉진법’ 제27조의 근거에 의거 민간주택에 설치하는 태양광 설비 일부를 지원하는 사업을
시행하고 있다. 지원하는 있는 주택용 태양광 발전설비는 쓰다 남은 전기를 한전으로 역송전하여 보관하다가 밤이나 흐린 날에 되찾아 쓰는 계통연계형 시스템이다.
현재 보급되고 있는 계통연계형 설비는 태양전지판과 인버터만으로 구성되어 실시간으로 발전되는 전력을 저장할 배터리가 없다. 그 결과 신재생에너지 보급률
확대에만 중점을 둔 현행의 태양광 주택 보급사업은 보급 규모가 확대될수록 기후에 따른 태양광 발전량의 변동이 국가적 규모에서 발생할 수 있으므로 한전은
급격한 공급 변동에 대응해야 한다.
이러한 문제점에 대응하려면 전력의 수요 및 공급 패턴을 제어할 수 있는 시장구조가 마련되어야 한다. 즉 한전의 발전 능력을 넘는 수요에 대응하기
위해서는 해당 시점에 전력을 공급하는 업체나 세대에 전력 단가를 높게 책정해주는 실시간 요금제를 시행해야 한다. 유럽에서는 국가 단위를 넘어서 발전회사들이
시장경제 원리에 의거하여 실시간으로 수요공급에 따라 단가가 수시로 변하는 실시간 요금제 시행을 위한 법안을 마련하고 있다.(1)
본 연구에서는 실시간 요금제의 시행을 전제로 가정용 태양광 전지와 인버터 이외에 배터리를 추가한 후 실시간 요금제 내에서 최저 비용으로 전력을 관리하는
마이크로 그리드 운용 알고리즘을 이차계획법(QP:Quadratic Programming)으로 설계한다.(2) 전력 수요 예측을 위하여 단독 주택의 열적 거동을 RC(Resistors and Capacitors) 모델로 근사시킨 후 벽체 및 실내 온도 거동을
미래의 기간에 대하여 예측제어(MPC; model predictive control)하는 구속조건을 적용하였다.(3)
2. EnergyPlus 기반 태양광 발전 주택 모델
2.1 주택 및 신재생에너지 설비 모델
Fig. 1은 건물 면적이 186 m2인 단독주택 모델을 나타낸다. 주택은 거실, 차고 및 다락의 3개 존으로 구성되며 거실 공간만 공조를 한다. 냉난방을 위해 지열 열펌프 설비를 적용하였으며
공칭 COP 3.5이다. 기후데이터는 EnergyPlus가 epw 포맷으로 제공하는 서울지역 자료를 적용하였다.
Fig. 1. Single family house model (a) cutaway (b) view from south.
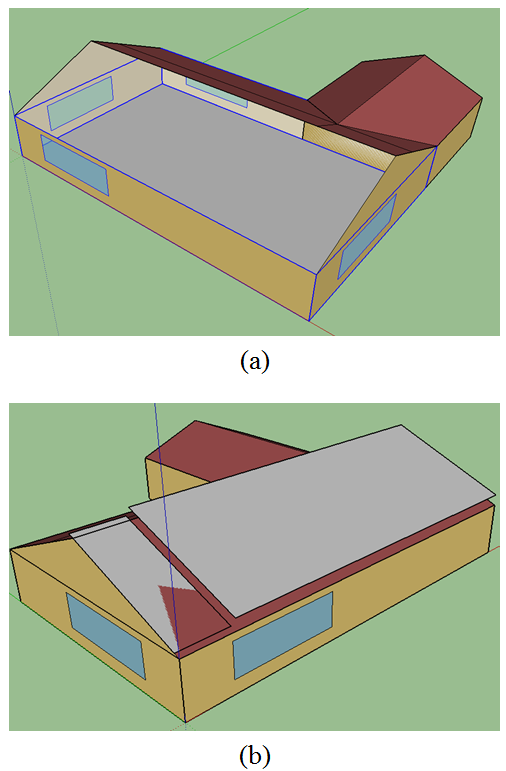
태양전지판은 남향에 위치한 지붕에 88.11 m2의 면적으로 설치하였다. 태양전지판 성능은 EnergyPlus DB에 구축되어 있는 BP Solar BP275 모델을 적용하였다.
2.2 최적운전을 위한 선형 모델 근사
Fig. 2는 Fig. 1의 EnergyPlus 주택 모델을 선형 RC 모델로 단순화한 구조를 나타낸다. 복잡한 구조의 건물도 열적 거동의 측면에서는 단순화된 RC 모델로
근사할 수 있다고 알려져 있다.(4) EnergyPlus의 시뮬레이션 결과를 유사하게 모사할 수 있는 Grey model의 RC 계수를 구하기 위하여 Matlab에서 제공하는 greyest라는
함수를 사용하였다. Fig. 2에는 열적 거동과 전력 관리가 통합되어 있는데, 주택 내 전력 관리시스템은 태양광 발전(PPV), 배터리(CB), 냉방전력 (Pac), 냉방을 제외한 가정 소비전력(Phome) 및 외부전력 (Pgrid)의 연결계통을 나타내고 있다. RC 모델의 열에너지 보존방정식은 다음과 같다.
Fig. 2. Linearized thermal model for optimal operation.
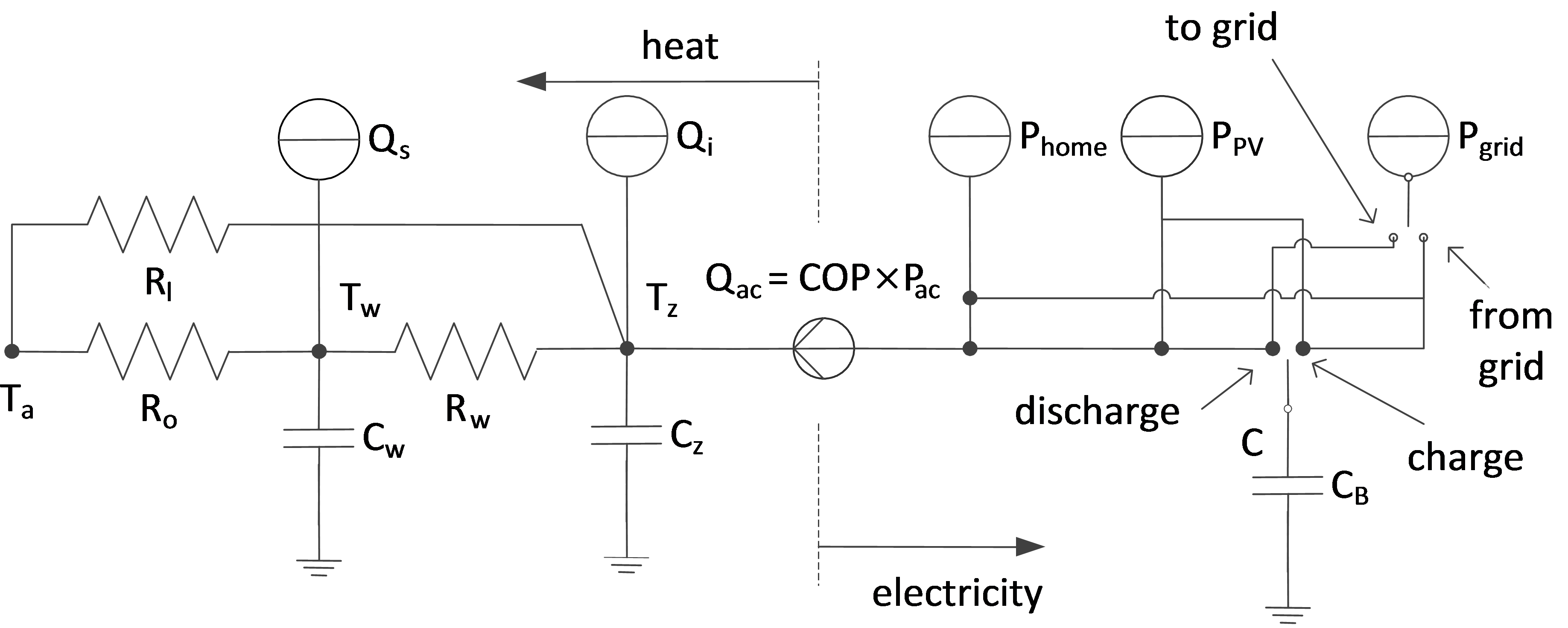
Fig. 3은 8월 1일부터 7일까지 서울 지역의 단독주택에 입력되는 외기온도, 일사량, 내부발열 및 냉방 열원에 대한 벽체와 거실 공간 공기 온도의 거동을
나타낸다. 벽체온도는 EnergyPlus 계산결과의 거실 4개 벽체와 천정의 내외부면 온도를 평균한 값이다. 외벽의 온도는 일사의 영향을 많이 받아
35℃ 이상으로 가열된다. 8월 4일에는 일사량이 적고 외기온도가 낮은 이유는 매우 흐리거나 비가 오는 날이기 때문이다. 결과에서 알 수 있듯이 실내
온도의 경우 위상차가 존재하나 전체적으로 양호한 동적 거동을 나타내고 있다. Fig. 3의 모사성능을 나타낸 RC 모델을 대상으로 최적운전 알고리즘을 설계하였다.
Fig. 3. (a) Input variables to the RC model (b) Comparison of outputs of EnergyPlus and the RC model.
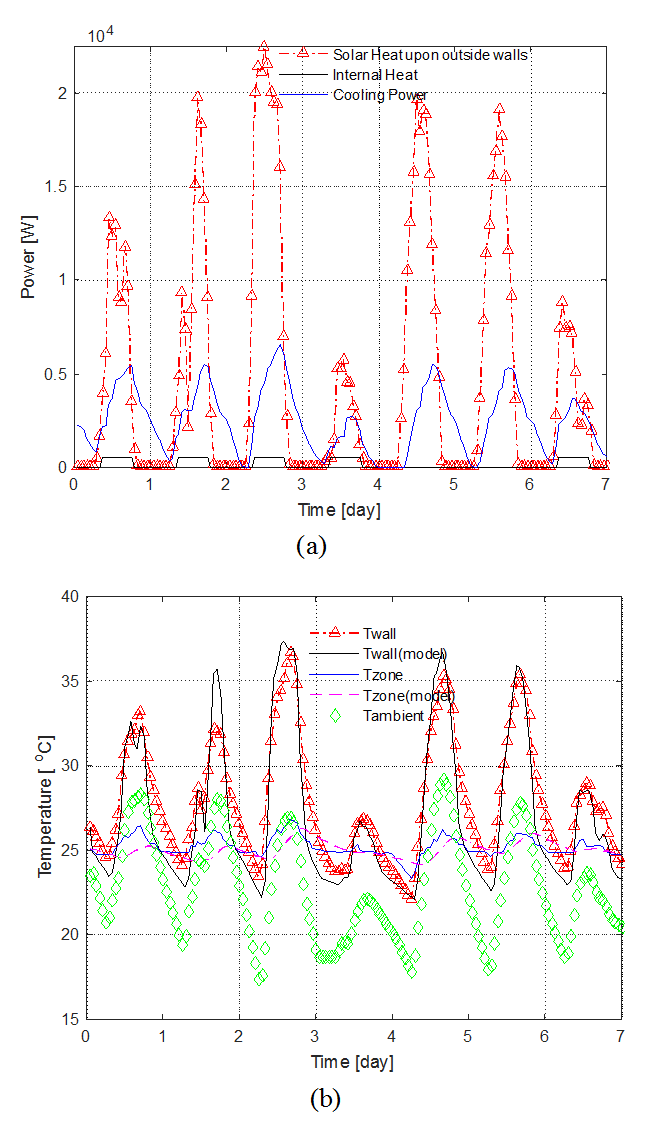
3. 최적화 운전 알고리즘
3.1 최적화 전제조건
알고리즘을 세대용 마이크로 그리드 마이크로 프로세서에 적용하기 위해서는 계산 부하가 작고 안정성이 있어야 한다. 그러한 관점에서 단시간에 최적해를
구할 수 있는 실시간성이 확보되어야 한다. 또한 최적운전은 다양한 목표를 동시에 최적화할수록 실용적 가치가 높다. 본 연구에서는 실내 온도를 설정온도의
허용 오차범위 내로 유지하면서 전력비용을 최소화하는 냉방운전과 전력비용을 최소화하는 신재생에너지 설비운전을 동시에 추구하는 전략 알고리즘을 개발하고자
한다.
전력비용은 다음의 실시간 요금제를 적용하기로 한다. 실시간 요금제는 스마트 그리드 사업의 활성화를 위한 핵심사안이다.(5-6)
최적운전이란 미래 기간 동안의 설비운전 전략을 계획하는 것이므로 미래에 발생할 외기온도와 일사량의 예측정밀도가 중요하다. 이러한 변수의 미래를 예측하는
것은 본 연구의 범위를 넘어서므로 일단 미래기간 동안의 외기온도와 일사량은 정확히 알려져 있다고 가정하기로 한다.
3.2 이차계획법의 설계
이차계획법(Quadratic Programming:QP)의 목적함수는 전력비용과 실내 온도 오차를 동시에 최소화하는 것이다. 이차계획법을 적용한
이유는 비용함수 중 온도오차는 크기를 최소화해야 하므로 제곱의 형태를 갖기 때문에 적용되었다. 이차계획법 비용함수 의 표준형은 다음과 같다.
여기서
위의 비용함수를 최소화하면서 미래의 일주일에 대하여 결정해야 할 의사결정변수벡터 x는 다음과 같다.
벡터 x중 {Tw, e, Pac}는 실내 온도 제어와 관련되어 있고 나머지는 전력관리와 관련된 의사결정 변수들이다. 이차계획법을 풀기 위해서는 다음의 선형구속조건이 적합하게 서술되어야
한다.
다음의 부등식은 전력의 수요와 공급의 균형을 표현한다. 수요와 공급이 모든 시간에 대하여 일치하는 것은 가혹한 조건이라 최적해가 존재하지 않는다.
따라서 과잉전력량(EPS:Excessive Power Supply)을 1 [W]로 하여 수요공급 편차의 상한과 하한을 설정하였다.
한편 구속조건으로서의 독립된 등식은 3개이다. 처음의 2개는 식(1), 식(2)를 이산형으로 표현한 것이고 다른 하나는 배터리의 충전과 관련된 것으로서 다음과 같다.
위 식에서 배터리에 충전된 전하량 C는 시간당
만큼의 자기방전이 일어나고 충전된 전하를 방전시켜 사용할 때는 (1-
)만큼의 방전손실이 발생한다.
최소 비용함수를 충족하는 의사결정변수들을 찾으려면 식(9)와 같이 변수들의 상한과 하한의 범위를 지정해야 한다.
다음의 식은 배터리 내 충전량의 하한과 상한을 나타낸다. DODmax는 최대 방전깊이이다.
충전 및 방전 전력의 상한은 배터리의 최대 충방전율에 의해 결정된다.
본 연구에서 설정한 x의 범위는 다음과 같다.
4. 최적화 계산 결과
Fig. 4와 Fig. 5는 에 대한 최적화 계산결과이다. Fig. 4(a)에 따르면 실내 온도는 설정온도인 26℃를 비교적 잘 추종하고 있으며 벽체 온도의 거동에 따라 Fig. 4(b)의 전력 수요도 유사한 거동을 보이고 있음을 알 수 있다. 전력 수요의 대부분은 냉방전력 수요이며 전력 공급과 균형을 잘 이루어 식(10)과 식(11)의 구속조건을 충족하고 있음을 보여준다. Fig. 4(c)는 전력 수요 관리의 결과를 나타낸다. 결과에 따르면 전력요금이 비싼 낮 시간에는 발전된 태양광뿐만 아니라 배터리에 저장된 전력도 광역전력망으로 역송전하여
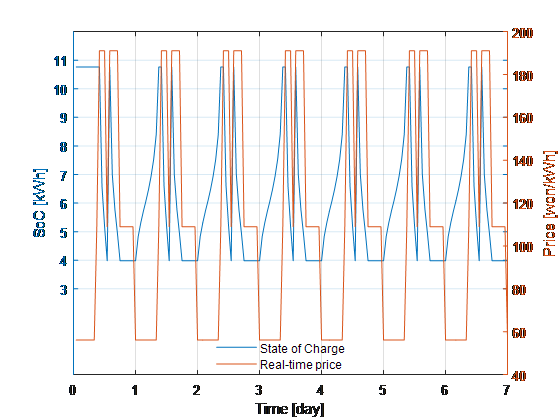
판매하고 있다. 단 점심시간인 12시부터 오후 1시 그리고 저녁과 심야에는 전력단가가 저렴하여 역송전을 줄이고 오히려 배터리에 충전하고 있다. Fig. 5는 배터리 충전상태를 나타내는데 전력요금이 저렴할 때 충전했다가 낮에 광역전력망에 되파는 구조를 실시간 요금제와 비교하여 보여주고 있다. 충전량의
상한과 하한은 식(13)에 서술된 결과를 따르고 있다.
Fig. 4. Optimization result with =1 (a) Indoor temperature (b) Demand-supply matching (c) Electric power management.
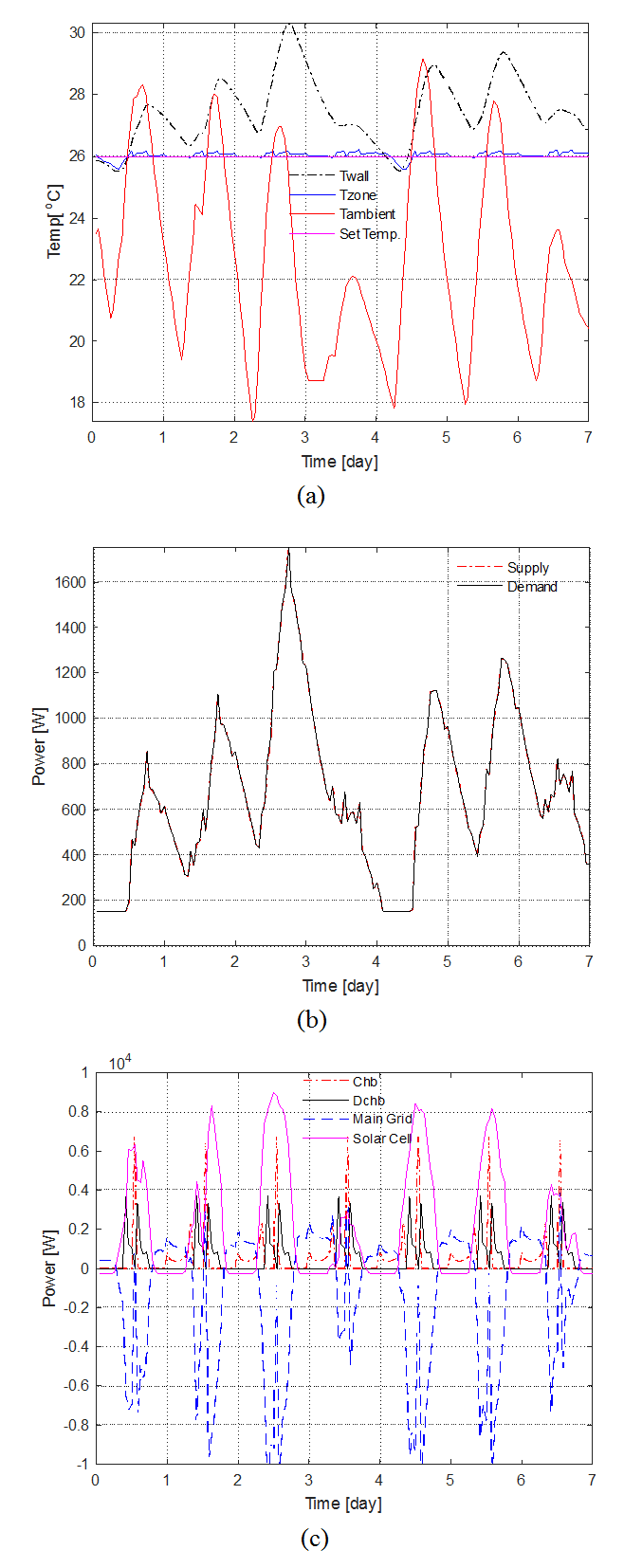
Fig. 5. Battery SoC with =1 and real-time pricing.
경제성 증대를 위해서는 현재의 배터리 용량이 적합한 설계인지 평가가 필요하다.
이제 가중치 β2를 조정하면서 냉방온도 오차 허용 폭에 따라 전력량과 비용이 어떻게 절감되는지 파악하여 보았다. Fig. 6은 그 결과의 일부를 나타낸다. Fig. 6(a)는 β2가 0.1인 경우로서 온도오차가 최대 2℃ 정도가 되는 경우도 나타나고 있다. 이러한 결과를 table 1과 같이 정리하였다. table 1은 8월 1일부터 일주일간의 최적운전 결과에 따른 온도오차의 표준편차, 냉방 소비전력량 그리고 순전력비용을 β2의 크기에 따라 보여주고 있다.
Fig. 6. Indoor temperature with (a) β2=0.1 (b) β2=10.
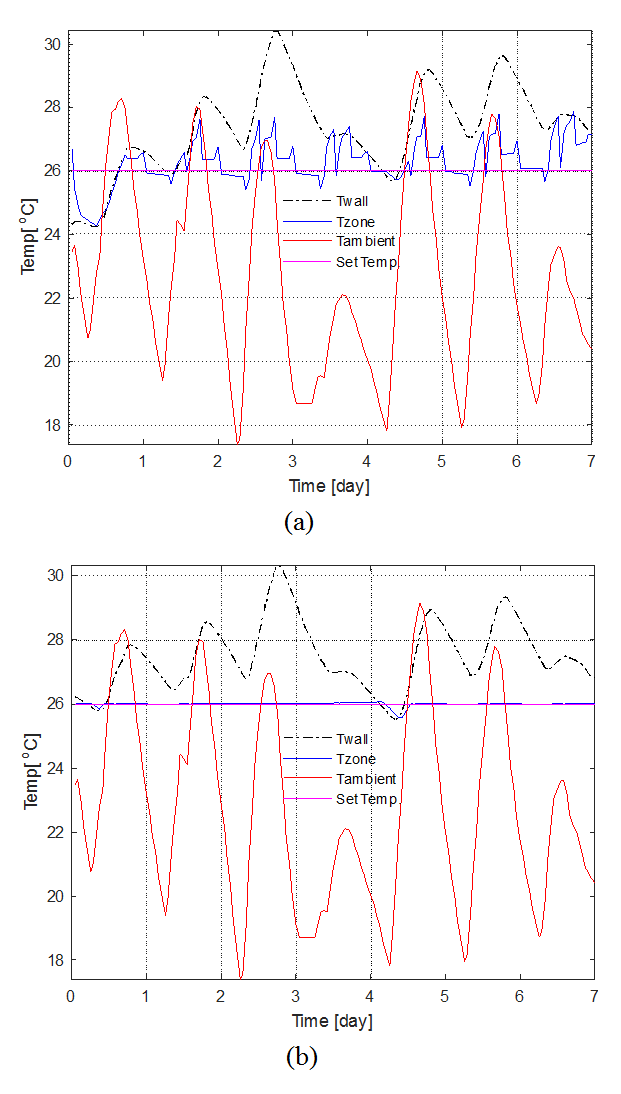
Table 1. Performances according to β2
|
β2
|
Standard deviation of e[℃]
|
Wac[kWh]
|
cost [won]
|
|
0.1
|
0.7132
|
68.23
|
-59,425
|
|
1
|
0.1162
|
87.36
|
-55,634
|
|
10
|
0.0690
|
90.88
|
-55,004
|
결과에 따르면 전력량 절감효과는 β2가 1에서 0.1로 변경되었을 때 크게 나타난다. 실내 온도 오차는 다소 증가하여 Fig. 6(a)와 같이 일시적으로 28℃ 근처로 접근하는 경우는 있지만 비교적 쾌적한 온도범위를 유지하고 있다. 이 경우에는 전력요금이 저렴한 시간대에 실내 온도를
다소 과냉하여 벽체 축열을 활용하고 전력요금이 비쌀 때는 실내 온도를 허용온도 범위 한계 근처까지 올려 냉방소비 전력량을 줄이는 전략을 구사하고 있다.
반면에 β2가 10인 경우에는 Fig. 6(b)와 같이 실내 온도는 설정값과 거의 일치하게 제어하는 것의 가중치가 높기 때문에 전력 절약운전을 수행할 수가 없다. 그 결과 β2가 0.1인 경우는 10인 경우에 비하여 75%의 전력량 사용하고 있으며 실시간 요금제를 적용하면 일주일간 4,437원이 절감되는 것이다. table 1에서 전력요금이 (-)값인 이유는 광역전력망으로의 역송전 결과 수익금이 된 것을 의미한다. β2가 0.1인 경우와 10인 경우의 수익금 차이는 에어컨 절약운전에 따른 절감액과 유사하다.
5. 결 론
본 연구에서는 미래에 보편화될 실시간 요금제를 가정하여 공급측의 유연성 개선을 위해 배터리를 사용한 경우의 최적 운전 전략에 관해 이차계획법에 기반한
최적화 운전 전략을 적용하여 다음과 같은 결론을 얻었다.
(1) 단독세대의 냉방부하를 선형 RC 모델로 근사하여 예측제어의 구속조건으로 적용할 수 있다.
(2) 실내 온도 제어를 수행하면서 전력비용을 최소화할 수 있는 예측제어 운전이 이차계획법에 의해 가능함을 확인하였다.
(3) 본 연구를 통해 파악된 구속조건들이 실용적인 이차계획법 설계에 적용될 수 있음을 확인하였다.
후 기
본 연구는 한국에너지기술연구원의 주요사업으로 수행한 결과입니다(B6-2429).
References
2013, Commission for Energy Regulation, CER National Smart Metering Programme Time
of Use Tariffs Mandate, CER/13/152, www.cer.ie

, https://en.wikipedia.org/wiki/Quadratic_progr amming
Deng K., Sun Y., Li S., Lu Y., Brouwer J., Mehta P. G., Zhou M., Chakraborty A., 2015,
Model Predictive Control of Central Chiller Plant With Thermal Energy Storage Via
Dynamic Programming and Mixed-Integer Linear Programming, Ieee Transactions on Automation
Science and EngiNeering, Vol. 12, No. 2, pp. 565-579

Harish V. S. K. V., Kumar A., 2016, Reduced order modeling and parameter identification
of a building energy system model through an optimization routine, Applied Energy,
Vol. 162, pp. 1010-1023

Kim S. D., 2012, Study on a phase-in strategy of introducing time of use pricing,
Korea Research Council for Electric Power Industry.

K-MEG Project , G-Valley Smart Energy Management Service, http://g-vally.k-meg.org/tou.html
