Park Seung-Hoon
(박승훈)
1
Lee Hyun-Soo
(이현수)
1
Jang Young-Sung
(장용성)
2
Kim Eui-Jong
(김의종)
3†
-
Department of Architectural Engineering, Graduate school, Inha University, Incheon,
22212, Korea
(인하대학교 건축공학과 대학원)
-
GS E&C Building Science Research Team, Yongin, 17130, Korea
(GS건설)
-
Department of Architectural Engineering, Inha University, Incheon, 22212, Korea
(인하대학교 건축공학과)
Copyright © 2016, Society of Air-Conditioning and Refrigeration Engineers of Korea
keywords
DST-Duct STorage, EWT-Entering Water Temperature, BHE-Borehole heat exchanger, Optimization algorithm, TRNSYS
키워드
DST 모델, 보어홀 출구온도, 지중열 교환기, 최적화 알고리즘, 트랜시스
기호설명
B:지중열교환기의 간격 [m]
EWT:지중열교환기의 출구온도 [℃]
H:각 지중열교환기의 깊이 [m]
L:지중열교환기의 전체 길이 [m]
N:지중열교환기의 개수
R:열 저항 [mK/W]
T:온도 [℃]
V:체적 [m³]
g:함수
q:부하 [W]
l:상계
u:하계
x:설계변수
하첨자
DST:지중 열 저장고(Dust STorage)
g:지중
h:단위 시간 최대 부하
6h:6시간 열 펄스
m:최대 부하가 발생하는 달의 평균값
1m:한 달간의 열 펄스
y:연 평균
10y:10년간의 열 펄스
p:온도 보정 값(temperature penalty)
set:설계 값
1. 서론
지중의 안정적인 온도를 이용하여 열펌프의 효율을 높인 지중열 히트펌프 시스템은 동시에 신재생에너지 설비로 간주되어 많은 관심을 받고 있다.(1)
지중열 히트펌프 시스템은 열펌프와 건물 주변에 설치되는 지중열교환기로 구성된다. 지중열교환기 내부를 순환 후 열펌프로 유입되는 유체온도(EWT-Entering
Water Temperature)는 열펌프의 성능을 결정하는 주요 인자이며, 동일한 지중 부하조건에서도 지중열교환기의 개수 및 배열 간격, 지중 특성에
따라 값이 달라진다. 일반적으로 EWT의 최대 거동 범위는 시스템 설계자에 의도에 의해 결정되며, 설계 시 최소 10년 이상의 장기간 시스템 운전
조건에서 EWT 거동이 설계 범위 내에서 유지되는지 파악하는 것이 중요하다. 일반적으로 지중열교환기를 과잉으로 설계하면 설계자가 정한 EWT의 최대
및 최소 범위에 동떨어져 설계의도를 반영하지 못하고 초기 투자비 상승을 초래한다. 반면, 자칫 지나치게 축소된 길이로 설계하게 되면 EWT가 설계
범위를 넘어서고 경우에 따라서는 열펌프 수용 범위를 넘어서 시스템이 제대로 작동하지 않게 되는 문제를 야기하게 된다.
따라서 장기간 운전 상황에서 EWT가 설계 조건에 근접하도록 지중열교환기 배열과 길이를 결정하는 것이 일반적인 설계 과정이며, 복잡한 물리적 특성을
고려한 해석이 필요하다.
기존에 주로 사용되었던 설계방법은 다수의 지중열교환기를 설계하기 위해 비교적 분석이 쉬운 단일 지중열교환기를 가정하고 여기에 가중 길이를 더하는
방식을 사용하거나 다수 지중열 교환기를 직접 묘사하는 방식을 이용한다. 후자는 Eskilson(2)에 의해 제안되었던 지열 응답함수(g-function)를 이용한다. 최근 지열 응답함수를 유도하기 위한 가정 조건에 따라 함수 값의 차이가 발생하는
등 응답함수 분석에 대한 연구도 함께 이루어지고 있다.(3)
위에서 언급한 방법을 사용한 기존 설계 도구들은 일반적인 지중열교환기 설계 목적으로 사용되고 있다.
한편, 설계된 지중열 히트펌프의 제어 및 시스템 분석을 위해서는 에너지플러스나 트랜시스와 같이 정밀한 에너지 해석도구가 필요하며 이 경우 앞선 설계도구를
이용하여 계산된 지중열교환기 정보를 다시 해석도구 내에 다시 구현해야한다. 또한 기존 설계 도구의 경우 시스템의 구성이 복잡해지고 축열 등 새로운
형태의 지중열 히트펌프 시스템들을 해석하기 위해서는 별도의 세심한 가정과 파라미터 설정이 요구된다.
따라서 자유로운 시스템 구성이 가능한 시뮬레이션 도구에 지중열교환기 설계 기능을 포함시킨다면 향후 활용성이 클 것으로 예상된다.
이에 따라 본 연구에서는 트랜시스 내부 지중열교환기 모델(DST-Duct Storage)과 트랜시스에서 제공하는 최적화 도구인 TRNOPT(4)를 이용하여 시뮬레이션 기반의 지중열교환기 설계방법을 제시하고, 그 결과를 ASHRAE(5)가 제공하는 지중열교환기 설계 도구의 결과와 비교하고자 한다.
2. ASHRAE 설계 방법
ASHRAE에서 제안하는 지중열교환기 설계 방법은 아래 식(1)과 같다. L은 지중열교환기의 전체 길이를 나타낸다. 아래의 q와 R은 각각 지중 부하와 열 저항을 나타내다. qh는 단위 시간에 발생하는 최대 부하에 해당하는 펄스이며, qm은 최대 부하가 발생하는 달의 평균 부하 값, qy는 연 평균 부하 값을 의미한다. Rb는 보어 홀의 열 저항을 의미하고 R6h는 6시간동안 최대부하가 발생할 때의 열 저항을 나타낸다. R1m 및 R10y는 각각 한 달, 10년 간 열 펄스에 해당하는 열 저항이다. 분모 첫 번째 항은 지중열교환기 작동 유체의 평균 온도로 EWT와 LWT(Leaving
Water Temperature)의 중간 값으로 가정할 수 있다. EWT와 LWT는 열펌프와 지중열교환기 사이에서 순환 관계에 있으므로 EWT와 LWT는
계산을 통해 동시에 얻을 수 있다. Tg 는 초기 평균 지중 온도이다. Tp는 지중열교환기 사이의 열 간섭에 의한 온도 보상 값(temperature penalty)을 의미하며 ASHRAE에서는 배열에 따라 근사치를 제안하고
있다. 근사치에 따른 오차를 줄이기 위해 g-function을 이용하여 Tp를 계산하거나(6), 많은 데이터로부터 회귀식을 유도하여 계산의 정확성을 높여 식(1)을 사용하고 있다.
식(1)에 나타난 것처럼, 지중열교환기 모델링에 있어서 지중부하와 Tp, EWT, 열 저항 및 초기 지중온도 등의 설계 인자들은 지중열교환기 길이에 큰 영향을 주는 요소이다. 그러나, 초기 지중온도와 열 저항 및 지중부하는
주어진 건물 프로젝트와 지중 조건에 따라 자동적으로 결정되기 때문에 설계자가 정하는 EWT와 Tp에 의해 동일한 프로젝트에서도 전체 길이가 다양하게 나타날 수 있다. 연구에서는 EWT가 히트펌프 성능 범위를 초과하지 않는 범위 내에서 설정된 온도로
지중열 히트펌프 시스템이 장기간 안정적으로 운전되기 위한 지중열교환기 설계 값을 구하고자 한다.
3. 트랜시스를 이용한 설계 방법 제안
3.1 지중열교환기 모델
Hellström et al.(7) 이 제안한 열 저장 시스템 해석용 모델인 DST(Duct STorage) 모델은 현재 트랜시스 Type 557로 변환되어 TESS 라이브러리 형태로
제공되고 있다. 이 모델은 수치 모델과 해석 모델의 장점을 적절히 이용하여 구성되었기 때문에 해석적 모델에 비해서는 경계조건 등을 자유롭게 묘사하면서
비교적 빠르게 계산을 수행할 수 있다는 장점이 있다. 해당 모델은 다수의 지중열교환기를 Fig. 1과 같이 일정 간격의 실린더형 배열을 대상으로 한다. 즉, 사용자가 지중열교환기 간격, 개수, 길이에 대한 값을 설정하면 DST 모델은 식(2)와 같이 지중의 저장 부피를 계산하고 지중열교환기 배열을 일정하게 분배하게 된다.
Fig. 1. Schematic of the 19 boreholes configuration in the DST model.
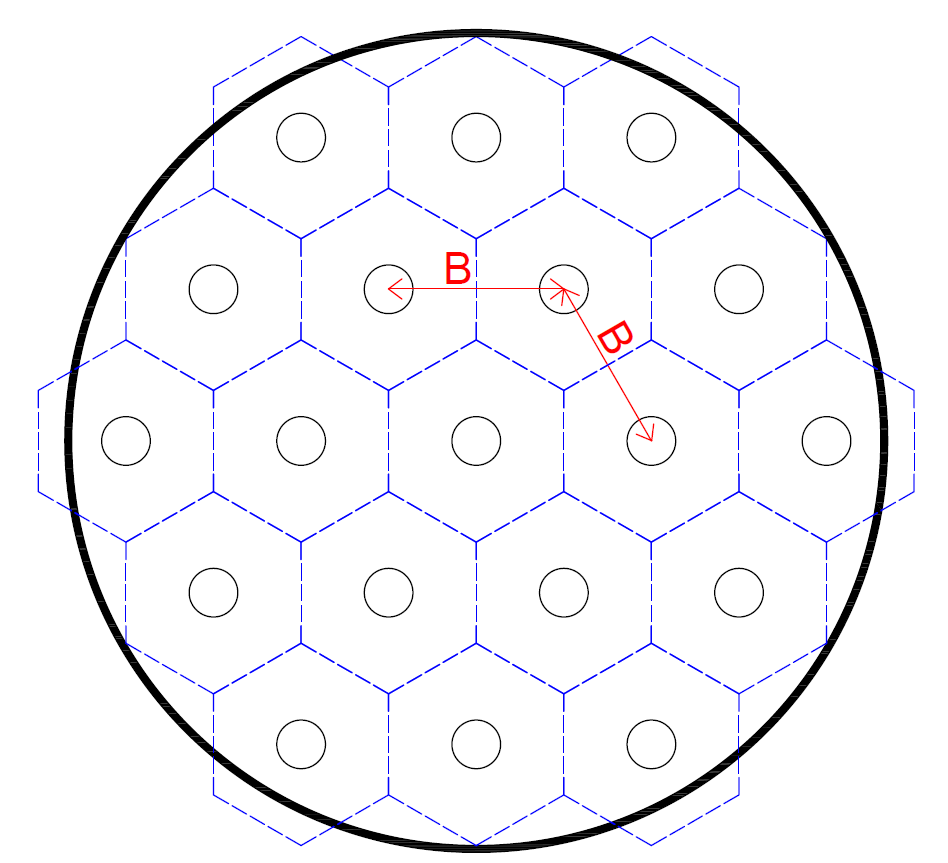
DST 모델의 이와 같은 배열 제한 문제는 비정형 배열 등 실제 프로젝트에 직접 적용하기 쉽지 않으나 식(2)의 VDST에 배열 방식에 따라 적절한 가중 계수를 사용하면 오차를 줄일 수 있다. 한 예로 Bertagnolio et al.(8)는 I자형 배열에 대해서 VDST를 계산하는 새로운 식을 제안하였다. 본 연구에서는 DST 모델을 이용한 설계 방법 제안 가능성을 확인하는데 초점을
맞추어 기존 균일 배열 조건에 대해서만 연구를 진행하였다.
3.2 최적화 알고리즘 TRNOPT
최적 계산법은 현재까지도 여러 분야에서 다양한 목적으로 사용되고 있다.(9,10) 본 연구에서는 지중열교환기의 최적 모델링을 위해 트랜시스에 포함된 TRNOPT를 사용하고, 내부 최적 알고리즘 중 좌표 추정 방법(Coordinate
research method)을 이용하였다. 이 방법은 설계변수, 목적함수 및 제약조건을 정의하여 목적함수의 값이 최소가 될 때의 설계변수(x)를
찾도록 계산을 수행하는 일반적인 최적화 과정을 사용한다. 설계변수 x는 집합 X에 대한 l(상계), u(하계) 범위를 정의하여 제약조건을 설정하였다.
목적함수가 위의 제약조건을 만족하면서 최솟값을 가질 때의 설계변수를 추적하게 된다. 이를 정리하면 식(3)과 같다.
최적화 알고리즘을 통해 다수의 설계변수에 대해 최적의 결과를 찾을 수 있다. 위와 같은 최적화 알고리즘을 지중열교환기 길이 설계에 응용하면 10년
후 지중열교환기의 출구온도(EWT)가 설계온도와 가장 근접하게 될 때의 지중열교환기의 개수(N)와 교환기 길이(H)를 최적화 알고리즘을 통해 찾을
수 있다. 지중열교환기의 전체 길이(L)는 N과 H의 곱으로 표현된다.
4. 시뮬레이션 결과 및 검증
4.1 시뮬레이션 조건
본 연구에서 제안하는 최적화 알고리즘을 이용한 설계 방법을 검증하기 위해 table 1과 같이 대상 건물 및 지중열교환기 조건을 설정하였다. 본 연구에서는 각 지중열교환기의 깊이(H)값을 각각 150 m로 고정시키고 최적화 작업을 진행하였다.
Table 1. Simulation parameters for sizing of vertical borehole heat exchangers
|
Parameters
|
Values
|
|
Building
|
|
Floor area[㎡]
|
84
|
|
Number of households
|
120
|
|
Daily peak heating load[kW]
|
293
|
|
Heating HP COP
|
3.5
|
|
Cooling HP COP
|
4.5
|
|
Borehole
|
|
Borehole unit length[m]
|
150
|
|
Borehole distance[m]
|
5
|
|
Header depth[m]
|
1
|
|
Design EWT[℃]
|
30
|
|
Fluid specific heat[J/kg K]
|
3960
|
|
Borehole mass flow rate[kg/s]
|
0.2/unit
|
|
Pipe thermal conductivity[W/mK]
|
0.4
|
|
Grout thermal conductivity[W/mK]
|
2
|
|
Borehole radius[mm]
|
55
|
|
Borehole inner/outer radius[mm]
|
13/16
|
|
Center-to-center distance[mm]
|
47.1
|
|
Ground characteristics
|
|
Thermal conductivity[W/mK]
|
2
|
|
Thermal diffusivity[㎡/day]
|
0.08
|
|
Initial ground temperature[℃]
|
10
|
|
Simulation period[yr]
|
10
|
지중부하는 건물부하와 히트펌프 성적계수(COP)로부터 계산할 수 있으며 Kim(11) 연구에서 상세히 언급되었다. table 1에 나타난 것처럼 건물부하는 84 m2의 공동주택 120세대를 대상으로 계산하였다. 기상데이터는 서울의 TRY 기상 데이터를 사용하였고 냉방 및 난방 설정온도는 각각 26℃와 22℃를
적용하였다.
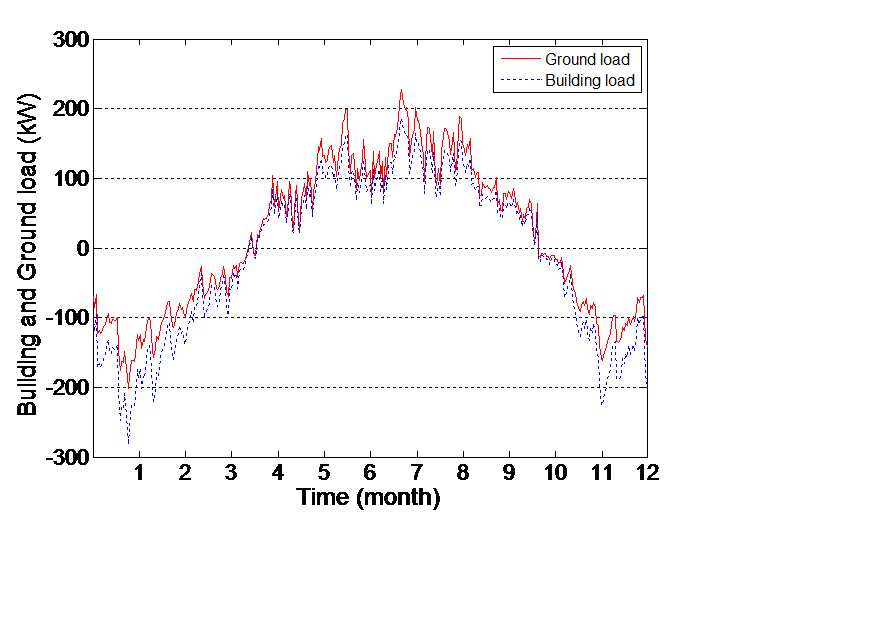
대상 건물은 아래 Fig. 2처럼 건물 부하로 볼 때 난방이 우세한 건물이지만 열 펌프와의 물리적 관계에 의해 지중부하는 최대 냉방부하 389 kW로 냉방이 우세하다. 그림에서
연중 지중부하와 건물 부하는 하루 평균치를 나타내었고 냉방부하는 (+) 부호로, 난방부하는 (-) 부호로 표현하였다. 히트펌프의 열전달 방식에 따라
냉방기간에는 지중 부하 값이 건물 부하 보다 크며 난방기간에는 지중 부하 값이 더 작다.
Fig. 2. Daily building and ground loads.
일반적인 지중열교환기 깊이인 150 m를 단일 지중열교환기 길이로 가정하고 전체 길이 산정을 위해 지중열교환기 개수를 최적화 알고리즘을 통해 도출하고자
한다.
4.2 최적화 알고리즘을 이용한 지중열교환기 설계
최적화 알고리즘은 목적함수 f(x)의 값이 최솟값이 되는 설계변수를 반복계산을 통해 도출한다. 따라서 목적함수 f(x)는 DST 모델의 출력 값인
지중열교환기의 출구온도(EWT)를 사용하였고 설계변수 x는 지중열교환기의 개수(N)를 사용하였다. 이 때, 설계자가 EWT 설계온도(Tset)를 정하게 되면 최적화 알고리즘은 식(4) 에 따라 목적함수가 최솟값을 갖도록 설계변수를 추적하게 된다. 이로써 시뮬레이션을 통해 10년 후 지중열교환기의 EWT가 설계온도(Tset)에 도달하기 위한 지중열교환기 개수(N)의 적정 값을 최적화 알고리즘이 찾을 수 있게 된다.
최적화 계산 수행을 위해 필요한 입력 값 및 초기 값은 table 2와 같다.
Table 2. Input and initial values for optimizing
|
Variables
|
Classification
|
Value
|
|
Input Variable
|
B
|
constant
|
5 m
|
|
H
|
constant
|
150 m
|
|
Tset
|
constant
|
30℃
|
|
Initial Values
|
N
|
design variable
|
40
|
DST 모델을 이용하여 10년간의 시뮬레이션이 반복적으로 수행되며 각 시뮬레이션마다 TRNOPT는 설계변수 값을 수정하며 최적 값을 찾게 된다.
table 3은 각 지중열교환기의 깊이(H)가 정해졌을 때, 설계변수로 지정된 지중열교환기의 개수(N)를 찾는 최적화 계산 결과를 표로 간략히 나타낸 것이다.
Table 3. Optimization process and result
|
Simulation step
|
1
|
2
|
3
|
···
|
11
|
|
f(N)
|
2.50
|
4.23
|
0.30
|
···
|
0.15
|
|
L[m]
|
6,000
|
6,750
|
5,250
|
···
|
5,203
|
|
N
|
40
|
45
|
35
|
···
|
34.7
|
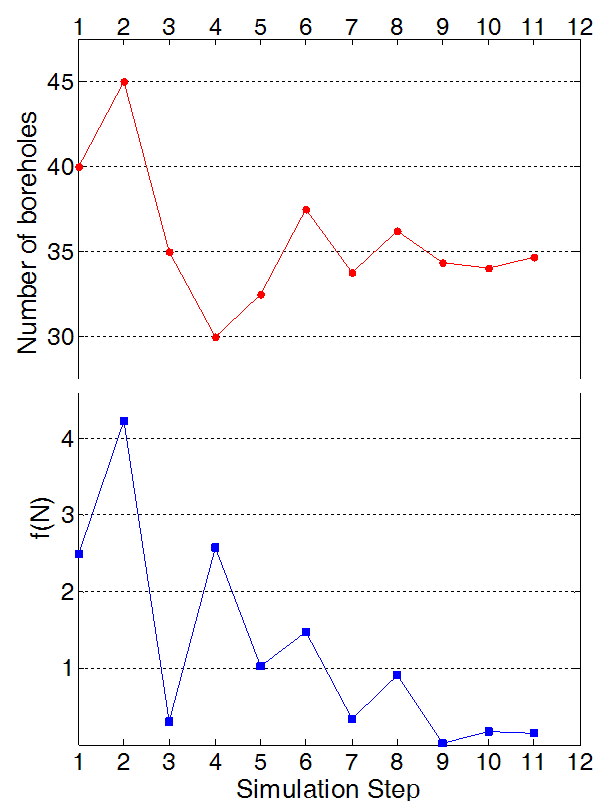
더불어 Fig. 3은 최적화 계산을 수행하는 TRNOPT의 계산 과정을 그래프로 나타낸 것이다. 최적화 계산을 수행하는 TRNOPT는 목적함수의 값이 최솟값이 되도록
하는 지중열교환기 개수(N)를 찾기 위해 11번의 계산 과정을 통해 값을 도출하였다.
Fig. 3. Optimization process with number of boreholes(red) and object function(blue).
얻어진 N값은 10년 후의 EWT가 설계온도인 30℃를 만족시키기 위해 필요한 지중열교환기의 개수는 최소 35개 이상이 되어야 한다는 것을 의미한다.
시뮬레이션 반복 계산 횟수는 초기 값 및 step size 등에 따라 달라질 수 있다.
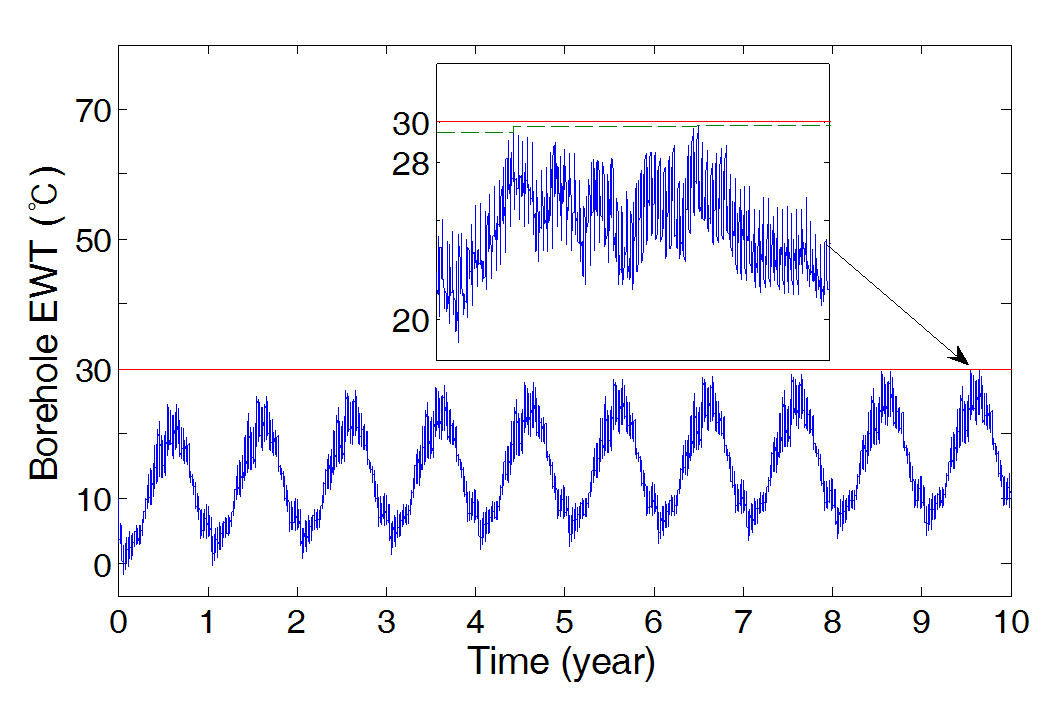
table 3의 결과로 얻어진 N값이 10년 동안의 EWT가 설계온도(Tset)와 근접한지를 검토하기 위하여 N값을 동일한 트랜시스 모델에 적용한 결과를 Fig. 4에 나타냈다. 그림에서 보는 바와 같이 10년 후 EWT가 설계온도와 비슷하다는 것을 알 수 있다.
Fig. 4. EWT evolution over 10 years.
이에 따라 추후 진행될 연구에서는 최적화를 통해 N, H의 두 가지 설계변수에 대한 최적화뿐만 아니라 B까지 포함된 설계변수에 대한 최적화도 제안할
수 있을 것으로 보인다.
4.3 ASHRAE 설계 도구와의 비교
ASHRAE가 제공하는 설계 도구는 지중열교환기 개수(N)와 지중열교환기 간격(B)을 입력하면 지중열교환기 깊이(H)를 계산하여 전체 길이(L)
값을 제공한다. 두 프로그램을 비교하기 위해, TRNOPT의 설계 변수를 앞서 설계변수로 설정했던 지중열교환기의 개수(N)를 각 지중열교환기의 깊이(H)로
변경하였다. 이로써 최적화 알고리즘은 단일 설계변수 H에 대해 최적 결과를 도출하게 된다.
table 4는 TRNOPT 최적화 알고리즘을 통해 얻어진 결과를 ASHRAE 설계 도구와 비교 한 것이다. 지중열교환기 전체길이(L)는 최적화 알고리즘의 결과가
5,375 m로 ASHRAE의 결과인 5,434 m와 비슷하게 나타났다. 각 지중열교환기의 깊이(H)는 전체 길이 L을 지중열교환기 개수(N)로 나눈
값이며, 마찬가지로 두 프로그램은 2 m의 오차만을 보였다.
Table 4. Comparison with the ASHRAE sizing tool
|
Tools
|
N
|
L(m)
|
H(m)
|
|
TRNOPT
|
40
|
5375
|
134
|
|
ASHRAE sizing tool
|
40
|
5434
|
136
|
5. 결 론
본 연구에서는 지중부하로 볼 때 냉방이 우세한 공동주택에 대하여 지중열 히트펌프 시스템을 운영하는 것으로 가정한 후, 최적화 알고리즘을 이용하여
시뮬레이션 기반의 수직형 지중열교환기 설계 방법을 제시하였다. 시뮬레이션 대상 기간은 10으로 설정하였으며 이 기간 동안 최적화 알고리즘이 지중열교환기
개수 혹은 길이를 변화시켜가면서 최대 EWT가 설계 EWT에 근접하는 값으로 길이 값이 수렴하도록 유도하였다. 이후 ASHRAE에서 제공하는 지중열교환기
설계 도구 결과와 비교하였다. 그 결과를 다음과 같이 정리하였다.
(1) 최적화 알고리즘을 이용하여 성공적으로 설계 EWT에 맞는 지중열교환기 길이를 도출할 수 있었으며, 계산된 길이를 역으로 파라미터로 설정하여
시뮬레이션을 수행하여 동일한 EWT를 확인할 수 있었다.
(2) 기존 도구와의 비교 실험에서 DST 모델의 지중열교환기의 전체 길이(L) 및 교환기의 깊이(H)는 각각 5,375 m, 134 m이고, ASHRAE
설계 도구의 결과는 각각 5,433 m, 136 m로 전체 길이에 대해 1.07%의 오차를 보였다.
(3) DST 모델은 N, H 중 자유롭게 설계 변수를 지정하여 최적화를 수행할 수 있었다.
본 연구에서 제안한 시뮬레이션 및 최적화 기반 지중열교환기 설계 방법은 향후 하이브리드 지중열 히트펌프와 같이 복잡하게 구성된 시스템의 설계 용도로
활용성이 클 것으로 기대한다.