Kim Min Ho
(김민호)
1
Lee Yong Tae
(이용태)
1
Chung Jae Dong
(정재동)
2†
-
Department of Mechanical Engineering, Graduate School of Sejong University, Seoul,
05006, Korea
(세종대학교 대학원 기계공학과)
-
Department of Mechanical Engineering, Sejong University, Seoul, 05006, Korea
(세종대학교 기계공학과)
Copyright © 2016, Society of Air-Conditioning and Refrigeration Engineers of Korea
keywords
Thermoplastic elastomer, Packing, Hot plate welding, Melting, Solidification
키워드
TPE, 패킹, 열판융착, 용융, 응고
기호설명
cp:비열 [J/kg·K]
f:액상분율
g:중력가속도 [m/s2]
H:엔탈피 [J/kg]
h:현열엔탈피 [J/kg]
k:열전도율 [W/m·K]
L:잠열 [J/kg]
P:압력 [Pa]
S:소스항
T:온도 [K]
t:시간 [s]
u:속도 [m/s]
β:열팽창계수 [1/K]
μ:점성계수 [kg/m·s]
ρ:밀도 [kg/m3]
x, y, z:좌표 [m]
X:길이 [m]
Y:높이 [m]
Z:폭 [m]
하첨자
i:초기
l:액체
m:녹는점
ref:기준
s:고체
w:벽
1. 서론
밀폐용기는 음식 및 다양한 물건들을 쉽고 신선하게 보관할 수 있어 활용범위가 넓어짐과 동시에 인체에 무해하며 성능이 좋은 용기에 대한 개발이 활발하게
이뤄지고 있다. 밀폐용기의 기능성과 디자인이 다양하게 개선되면서 밀폐용기 시장이 급성장하고 있다. 유리 및 도자기 재질의 제품이 생산되면서 국내를
넘어서 중국시장에서도 수요가 증가하는 추세이다. 시장의 급성장만큼이나 소비자들의 인체 유해성분에 대한 관심도 높아져 가격이 높더라도 인체에 무해한
소재를 이용한 제품의 관심이 높아지고 있다. 많은 소비자와 생산자의 초점은 밀폐용기의 재질에 맞춰져있다. 현재까지 각종 산업이나 가정집에 사용되는
밀폐용기의 패킹재질로서 고무, PVC 및 실리콘과 같은 재질이 사용되어왔다. 하지만 고무패킹은 역한 냄새를 발생한다거나 용기와 뚜껑이 붙어버리는 단점이
있다. 최근 밀폐용기의 재질이 플라스틱에서 유리로 추세가 많이 바뀌는 과정에서 기존 패킹이 밀폐용기와 들러붙는 문제가 더 부각되고 있다. 또한, 실리콘
패킹은 단가가 비싸며 열융착이 불가능하여 수작업에 의한 본드 접착으로 패킹을 만들어 자동화양산에 어려운 점이 있다. 증가하는 소비자들의 건강에 대한
니즈와 생산자의 자동화 양산에 대한 니즈를 충족시키기에는 기존의 패킹재질에는 이와 같은 여러 가지 문제점들이 있었다.
융착기술로는 열융착, 진동융착, 초음파융착 등이 적용된다. 열융착은 일반적인 접착공정보다 접착제 및 부수적인 유연제와 같은 부수적인 부 원료들이 필요
없기 때문에 생산비용이 적다. 또한 기계 장치가 비교적 저렴하며 공정과정 중에서 폐수처리가 불필요한 친환경적인 장점이 있다. 열융착에는 열과 압력을
이용하는 방법과 고온이 열풍을 이용한 방법 등이 이용된다. 본 연구에서는 인체에 무해한 열가소성 엘라스토머(Thermoplastic Elastomer;
TPE)를 이용하여 용융 시 발생하는 TPE의 열적 특성을 이해하고 열융착과정을 수치해석 하였다. 수치해석 통해 얻은 결과를 이용하여 자동화양산을
위한 최적조건을 찾았다. 자동화를 위한 최적조건을 찾는 것은 경험에 의존적이기 때문에 생산기술에 대한 불신을 초래할 수 있다. 패킹의 두께, 모양,
열판온도, 접촉저항 등의 영향을 고려하여 최적조건을 찾아 경쟁력이 있는 시스템을 구축하는 것이 본 연구의 목적이다. 최적화조건을 통해 단순 밀폐용기의
패킹뿐만 아니라 냉장고와 같은 전자제품 혹은, 다양한 제품의 밀폐 패킹의 자동화에도 적용할 수 있을 것이다.
2. 수치해석
2.1 해석방법
TPE의 열판용접(1-4)을 이용한 열융착과정은 Fig. 1과 같다. TPE의 단면은 2공 형태로서 두께는 하나의 TPE 패킹을 만들기 위해서는 긴 TPE을 링처럼 구부린 후 양 끝에 뜨거운 열판을 붙여 녹인다.
패킹의 끝이 경험적으로 0.2 mm 녹았을 때 열판을 떼고 패킹의 양끝을 붙인다. 녹은 패킹이 굳으면서 서로 붙어서 링의 형태로 하나의 패킹이 제조된다.
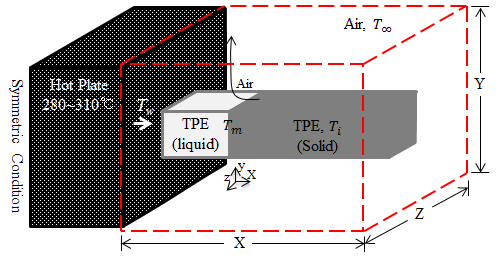
모델링을 위한 개략도는 Fig. 2에 도식했다. 자동화 시스템을 위한 TPE의 열융착은 용융이 일어난 후 다시 액상에서 고상으로의 응고가 일어나는 상변화현상을 포함하고 있다. TPE의
용융 및 응고 현상을 해석하기 위해 엔탈피방법을 도입했다. 엔탈피방법(5)의 지배방정식은 아래와 같으며 상용 CFD 프로그램인 STAR-CCM+v9.04를 이용했다.
Fig. 1. A schematics of hot plate welding process.
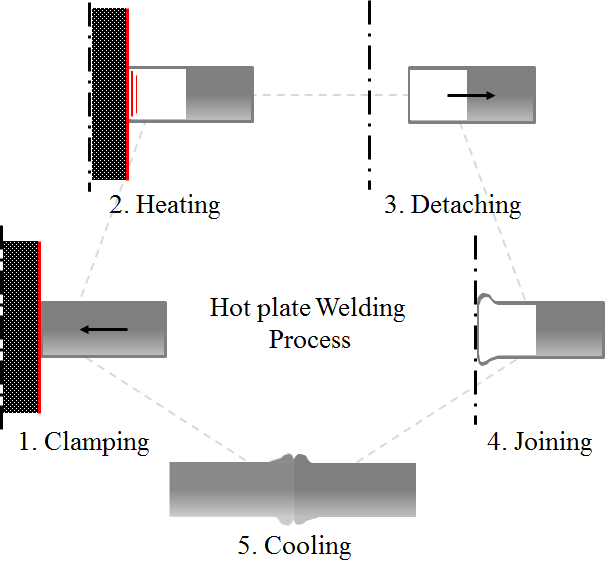
Fig. 2. Numerical model for hot plate welding.
식(2)의 우변 세 번째 항은 부력을 나타내는 항으로 녹은 액상의 밀도차이에 의한 자연대류를 온도차이로 근사하기 위해 Boussinesq 모델을 적용하였다.
식(2)의 생성항으로 추가된 S는 고상 영역의 속도를 0으로 만들기 위한 항으로 아래와 같이 Kozeny-Carman
식(6)으로 표현된다.
여기서 A는 액상분율(Liquid Fraction)을 의미하는 f의 함수로서
식(6)과 같이 온도의 함수로서 표현된다.
식(5)에서 C는 임의의 상수로 큰 값을 사용하며 일반적으로는 105~107이 사용된다. ε는 고상일 때 0으로 나눠지는 것을 방지하기 위함이다.
식(3)에서 엔탈피 H는 현열 엔탈피인
와 잠열 엔탈피인
의 합으로 나타낸다.
초기조건은 상온 25℃로 녹는점보다 낮기 때문에 패킹은 고상의 상태로 존재한다. 해석의 경계조건은 열융착과정이 용융과 응고, 두 과정이 포함되기 때문에
이를 고려하여 용융과정과 응고과정으로 나누어 설정하였다. 용융과정일 경우, 열판이 패킹의 끝이 맞닿아 끝으로부터 0.2 mm가 녹는 시간(t
m)까지 가해준다. 응고과정일 경우, 녹은 패킹의 양 끝을 붙이게 된다. 양 끝의 패킹이 온도 및 속도거동이 같다고 가정을 한다면 이는 대칭조건으로
볼 수 있다. 이를 식으로 표현하여 다음과 같으며 외부공기의 바깥 면에 대해서는 pressure outlet 조건을 적용함으로써 공기의 자유로운 유동을
모사했다.
Fig. 3. A cross section of TPE packing with three different types.

Continuity :
Momentum :
Energy :
2.2 물성치
본 연구에 사용된 TPE는 복합 폴리머 SEBS(Styrene-Ethylene-Butylene-Styrene)이다. SEBS의 열물성치에 대한 정보는
잘 알려져 있지 않다. 따라서 실제 패킹의 용융과정을 관찰 한 후에 나타나는 특징을 통해 물성치를 설정하고자 한다. 용융상태에서의 특징을 나열하면
다음과 같다.
(1) 뚜렷한 녹는점을 보이지 않는다.
(2) 용융 시, 비뉴톤(non-newtonian) 유체의 특성을 보인다.
(3) 변형이 적다.
복합 폴리머는 크게 Semi-crystalline 계열과 Amorphous 계열, 2가지로 분류된다. 이 둘을 나누는 기준은 결정도(crystallinity)이다.
결정도의 결과로서 나타나는 가장 큰 특징은 녹는점이다. 일반 물질은 단상에서 현열이 증가하다가 녹는점에 도달하여 잠열을 흡수하며 분자 구조가 바뀌면서
물질의 물성치가 바뀌게 되나, 복합 폴리머는 뚜렷한 녹는점이 존재하지 않는다. Amorphous의 경우, 현열이 증가하다 녹는점에 도달해도 일반 물질의
분자구조의 변화, 잠열 흡수와 같은 특별한 일이 일어나지 않는다. 그리고 가열된 만큼 현열이 계속 일정하게 증가한다. 다른 물성치의 경우, SEBS와
화학적으로 가장 결합성이 비슷한 Amorphous 계열의 Polystyrene로서 SEBS를 대체하여 수치해석을 진행하였다. 본 연구에 사용된 TPE의
물성치는
table 1에 나타냈다.
Table 1. Properties of Thermoplastic Elastomer
|
Property
|
Value
|
|
Melting Temperature [K]
|
180
|
|
Density [kg/m3]
|
1050
|
|
Thermal conductivity [W/m·K]
|
0.13
|
|
Specific heat [J/kg·K]
|
1793
|
|
Thermal expansion [1/K]
|
1.2 X 10-4
|
2.3 Non-Newtonian Fluid에 대한 해석방법
열가소성 엘라스토머는 비뉴톤유체로 점성계수와 녹는점에서 일반 뉴톤유체와는 다른 거동을 보인다. 비뉴톤유체는 용융하여 액상으로 존재할 때, 액상에서
일반 물질보다 상대적으로 높은 점성을 갖는다. 반면, 뉴톤유체는 shear rate에 상관없이 일정한 점성계수를 갖는다. 물질은 녹은 후, 액상 영역에서
자연대류가 발생하는데 발생한 자연대류에 의해 고상의 용융이 촉진된다. 이는 상경계면을 결정하는 주된 요인이 된다. Rayleigh수에 따라 차이는
있지만, 일반적으로 상변화현상에서 대류의 영향은 무시하지 못하며, 대류에 직접적인 영향을 끼치는 점성을 무시한 채 수치 해석을 하는 것은 정확도에
무리가 있다. 점성계수를 수치해석에 적용하기 위한 처리 방법은 여러 가지가 존재하지만 주로 점성계수가 shear rate의 함수인 동시에 온도의 함수로서
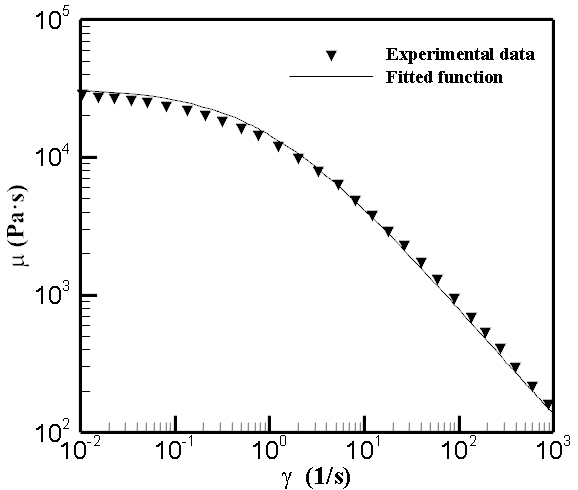
반영하는 형태가 일반적이다.(7-10) 본 연구에서는 점성에 대한 처리를 Fig. 4와 같이 실험 결과(11,12) 와의 곡선접합을 통해 shear rate의 함수인 상관식을 도출하여 적용하였다. 점성계수는 온도의 함수이기도 하지만 상온과 열판 온도의 평균인 약
200℃로 고정하여 오직 shear rate의 함수로만 정의하였다. 점성계수를 구하는 식은 아래와 같다.
Fig. 4. A Curve fitting with experimental data for viscosity.
2.4 변형에 대한 고찰
TPE를 하나의 패킹을 만드는 열융착 과정에서 용융과정과 응고과정을 거치게 된다. 이때, 외부로 용융물이 세어 나와 생기는 burr를 발생시킬 수
있다. 이는 불량으로 처리되기 때문에 패킹의 변형을 최대한 작게 해야 된다. 수치해석을 통해 용융과 응고 과정 중에 일어나는 burr의 생성가능성을
알아보았다. 해석은 간단하게 2차원 형상을 이용했으며 액상, 고상 그리고 공기로 다상으로 해석이 이뤄졌다. 좌측의 벽면으로부터 280℃로 1초간 가열되어
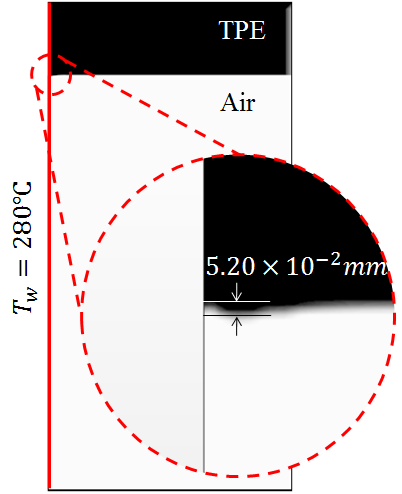
고상의 TPE가 녹는다. 그 후 대칭조건으로 바꾸어 액상이 된 TPE를 응고시킨 후 TPE와 공기와의 상경계면을 검토하였다. Fig. 5의 확대된 사진을 보면 고상의 TPE가 열융착과정을 거친 후 상경계면이 약간 튀어나왔지만 burr의 크기가 약 5.0×10-2 mm로 매우 작음을 확인할 수 있다. 일반적으로 상변화문제에서 고상의 모양을 결정하는 주된 요인은 액상에서 발생되는 자연대류의 강도이다. 경험적으로
TPE 끝단이 0.2 mm 녹은 후 열판을 떼고 패킹의 양끝을 붙이므로 자연대류가 발달하기에는 0.2 mm라는 간격은 너무 좁다. 또한, 비뉴톤유체의
특성상 점성계수가 커서 자연대류의 강도는 약하게 된다. 따라서 수치해석 결과에서와 같이 극히 작은 고상의 변형만이 발견되며, 이후 해석에서 burr의
발생은 고려하지 않아도 될 것으로 판단된다.
Fig. 5. Possibility of burr occrurrence.
3. 결과 및 고찰
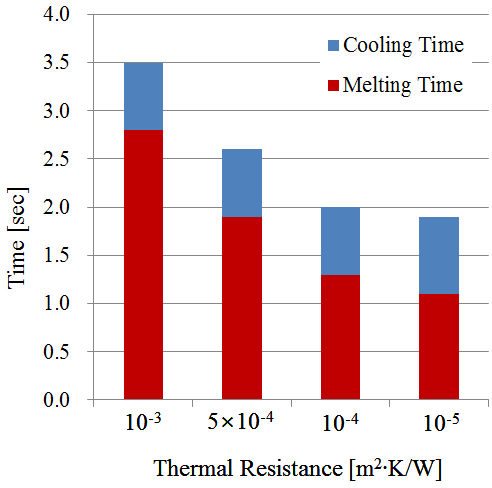
3.1 열판 온도 및 크기에 따른 영향
TPE의 자동화양산을 위한 최적화된 열판 온도를 찾기 위해 열판온도를 다양하게 바꾸어 TPE의 용융 및 응고 시간을 관찰함으로서 공정시간의 최적화
조건을 살펴보았다. 용융은 열판과 패킹이 맞닿는 곳에서부터 0.2 mm 녹을 때까지 진행되고, 이후 바로 열판이 제거되어 응고과정이 진행된다. 0.2
mm는 안정적인 융착과 패킹의 양 끝을 붙일 때 변형을 최소화하기 위해 현장에서 경험적으로 확립된 값이다. 열판의 온도는 녹는점인 180℃보다 높은
235℃~325℃으로 설정했다. 결과는 Fig. 6에 도시하였다. 열판온도에 따른 영향이 용융시간에 큰 영향을 주어 전체 시간차이를 만들지만 응고하는
시간은 열판온도의 영향이 작은 것을 알 수 있다. 최적화의 기준이 되는 1s 동안 0.2 mm가 녹는 열판의 온도는 280~295℃이다.
3.2 접촉저항에 따른 영향
TPE 패킹의 열융착을 해석할 때, TPE 가열부의 경계조건은 등온으로 해석하였다. 등온 경계조건은 열판과 TPE 사이의 열저항은 없는 것으로 이상적으로
가정하여 열판의 온도가 바로 TPE로 전도된다. 하지만, 실제 공정에서는 burr 발생을 억제하기 위해서 TPE가 녹을 때 압력을 가해서 눌러주는
것이 아니라 열판에 갖다 대는 수준으로 붙여주기 때문에 열판과 패킹 사이의 공기층으로 열저항이 존재한다. 접촉저항에 대한 값은 연구 자료가 부족하여
통상적인 값(10-3~10-5m
2·K/W)(13)으로 설정하여 그 영향을 비교하였다.
Fig. 7에 보이듯이 열저항이 공정시간에 미치는 영향은 무시할 수 없는 수준이다. 짧은 공정시간이 생산성에 미치는 영향을 고려할 때 생산자 입장에서는 접촉저항을
충분히 고려해야 할 것이다. burr 발생 억제와 접촉저항 감소라는 두 가지 상반된 목적을 위해 적절한 압력으로 TPE를 열판에 눌러서 접촉하여야
할 것이다.
Fig. 6. A melting and cooling time with different hot plate temperature.
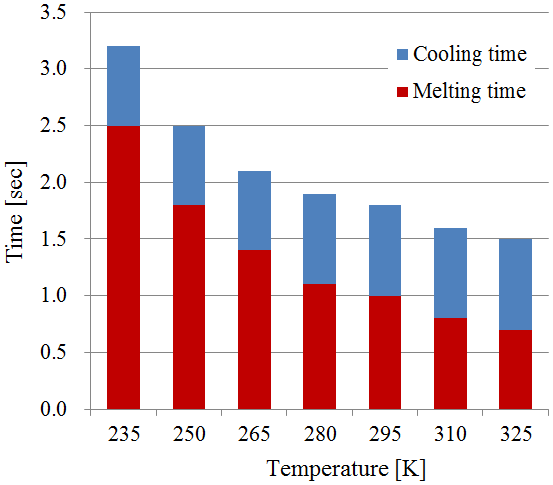
Fig. 7. A melting and cooling time with different thermal resistance.
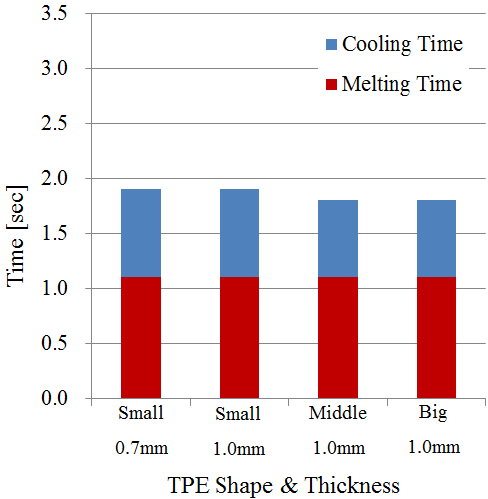
3.3 패킹의 모양과 두께에 따른 영향
본 연구는 자동화를 위한 최적조건을 찾고 이를 다양한 제품의 패킹 제작에 적용하기 위함이다. 다양한 모양에 대해서도 열융착이 미치는 영향을 알아보았다.
고려된 패킹의 모양은 Fig. 3에 나타냈다. 기본적으로는 2공 형태의 모양과 두께는 1 mm로 밀폐용기의 용도에 따라 달라지는 사이즈에 대응하기 위해 Small, Middle,
Big 사이즈로 나누었다. 또한 두께의 영향을 알아보기 위해 작은 사이즈(Small)의 두께를 0.7 mm로 제작된 패킹에 대해서도 해석을 실시했다.
열판의 온도의 경우는 1s 동안 0.2 mm가 녹는 280℃로 고정했다. Fig. 8은 열판온도와 열저항과는 다르게 모양과 두께에 따른 영향이 작은 것을 보여준다. 다른 고상에서 액상으로 변하는 상변화문제의 경우 액상에서 존재하는
자연대류에 의해 융해가 촉진된다. 본 연구에 사용된 패킹의 경우 비뉴톤유체의 성질을 갖고 0.2 mm라는 매우 짧은 길이이기 때문에 자연대류가 형성되지
못해 마치 1차원 전도처럼 패킹이 녹기 때문에 모양과 두께의 영향은 작은 것으로 판단된다.
Fig. 8. A melting and cooling time with different TPE shapes and thickness.
4. 결 론
본 연구에서 TPE 패킹의 열융착에 대한 연구를 수행하였다. TPE 패킹의 자동화 양산을 위한 최적조건을 찾기 위한 선행연구이다. SEBS의 열적
물성치가 잘 알려지지 않아 실제 TPE의 녹는 현상을 관찰한 후 물성치를 확립하고 자동화를 위한 최적 조건을 찾는 연구를 진행했다. TPE의 열융착을
용융과 응고과정이 포함된 상변화문제로 상변화문제를 해석하기 위해 엔탈피 방법이 사용되었다. 패킹의 모양, 두께, 열판 온도 접촉저항의 영향을 고려하여,
가장 큰 요인은 열판온도이며 자동화를 위한 조건인 1s 동안 0.2 mm가 녹는 열판온도가 약 280℃인 것을 발견했다. 뜨거운 열판과 TPE사이에
존재하는 열저항은 생산성에 크게 영향을 미치는 인자로 반드시 고려되어야 할 것이다. 하지만, TPE의 모양과 두께는 결과에 크게 영향을 끼치지 못하였다.
용융시간에 미치는 영향과는 달리, 선정된 4가지 인자 모두 응고 시간에는 크게 영향을 미치지 못한 것을 확인하였다.
후 기
본 연구는 중소기업청에서 수행하는 2015년도 기술혁신개발사업 혁신형기업과제의 일환으로 수행되었습니다.
References
Nieh J. Y., Ni J., Lee L. J., 1998, Hot plate welding of polypropylene. Part I : Crystallization
kinetics, Polymer Engineering and Science, Vol. 38, No. 7, pp. 1121-1132

Nieh J. Y., Ni J., Lee L. J., 1998, Hot plate welding of polypropylene. Part II :
Process simulation, Polymer Engineering and Science, Vol. 38, No. 7, pp. 1133-1141

Potente H., Schnieders J., Bornemann M., 2002, Theoretical model for the one-dimensional
temperature and stress calculation of simple hot plate welded geometries, Macromolecular
Materials and Engineering, Vol. 287, No. 11, pp. 843-853

Amanat N., James N. L., McKenzie D. R., 2010, Welding methods for joining thermoplastic
polymers for the hermetic enclosure of medical devices, Medical Engineering and Physics,
Vol. 32, No. 7, pp. 690-699

Swaminathan C. R., Voller V. R., 1992, A general enthalpy method for modeling solidification
process, Metallurgical Transactions B-Process Metallurgy, Vol. 23, No. 5, pp. 651-664

Carman P. C., 1937, Fluid flow through granular beds, Transactions of the Institution
of Chemocal Engineers, Vol. 15, pp. 150-166

Cross M. M., 1965, Rheology of non-Newtonian fluids : A new flow theories, Journal
of Colloid Science, Vol. 20, No. 5, pp. 417-437

Carreau P. J., 1972, Rheological equations from molecular network theories, Transactions
of the Society of Rheology, Vol. 16, No. 1, pp. 99-127

Yasuda K., 1979, Investigation of the analogies between viscometric and linear viscoelastic
properties of polystyrene fluids, Ph.D Thesis, Massachusetts Institute of Technology,
MA, U.S.A.

Escudier M. P., Poole R. J., Dales C., Nouar C., Desaubry C., Gresham L., Pullum L.,
2005, Observations of asymmetrical flow behaviour in transitional pipe flow of yield-stress
and other shear-thinning liquids, Journal of Non-Newtonian Fluid Mechanics, Vol. 127,
No. 2-3, pp. 143-155

Gujrati P. D., Leonov A. I., 2010, Modeling and simulation in polymers, Wiley-VCH
Verlag

Zepnik S., Kabasci S., Kopitzky R., Radusch H. J., Wodke T., 2013, Extensional flow
properties of externally plasticized cellulose acetate : Influence of plasticizer
content, Polymers, Vol. 5, No. 3, pp. 873-889

Incropera F. P., Dewitt D. P., Bergman T. L., Lavine A. S., 2006, Fundamentals of
heat and mass transfer 6th ed, Wiley
