Kwon Taeeun
(권태은)
1
Jeong Taeyoung
(정태영)
2†
Jeong Seokkwon
(정석권)
3
-
Graduate School of Refrigeration and Air Conditioning Engineering, Pukyong National
University(PKNU), Busan, 48547, Korea
(부경대학교 대학원 냉동공조공학과)
-
Training Ship, Pukyong National University(PKNU), Busan, 48513, Korea
(부경대학교 실습선)
-
Department of Refrigeration and Air Conditioning Engineering, Pukyong National University(PKNU),
Busan, 48547, Korea
(부경대학교 냉동공조공학과)
Copyright © 2016, Society of Air-Conditioning and Refrigeration Engineers of Korea
keywords
Optimized PI controller, Oil cooler, Variable rotating speed compressor, ITAE(Integral of Time-weighted Absolute Error), Temperature control
키워드
최적 PI 제어기, 오일쿨러, 가변속 압축기, 절대 오차 시간곱 적분, 온도제어
기호설명
Av:EEV 개도 지령[step]
C:제어기
Fi:인버터 주파수[Hz]
G:전달함수
K:이득상수
Ki:적분게인
Kp:비례게인
T*:설정온도 [℃]
To:오일출구온도 [℃]
Ts:과열도 [℃]
하첨자
1:압축기(compressor)
2:전자팽창밸브(Electronic Expansion Valve)
1. 서론
가변속 냉동시스템의 온도제어를 위한 제어기 설계법은 다수 제안되어 있다.(1-8) 그 중 전달함수 모델 기반의 PID 단독 제어는 설계가 쉽고 제어 성능이 뛰어나 실제 산업 현장에서 가장 널리 사용되고 있다.(1-4) 오일쿨러의 전달함수는 주로 특정 열평형 상태에서 섭동법으로 구해지며 짧은 부동작 시간(dead time)을 갖는 비선형 1차계로 모델링 된다.(9) 지금까지의 연구들 대부분은 이 비선형 시스템을 선형 1차계 모델로 근사화 하여 오일쿨러의 제어 성능 향상에만 설계 초점을 맞추었다. 이로 인해 설계
단계에서 무시한 부동작 시간의 영향 분석, 무시 가능한 부동작 시간의 범위, PI 게인에 대한 최적 성능 검토, 구축된 모델이 갖는 파라미터 불확실성에
대한 강인성 검토는 매우 불충분 하였다. 따라서 본 연구에서는 특정 평가기준을 적용한 PI 제어로직으로 설계사양과 최적 성능을 동시에 만족시키는 가변속
압축기 방식의 오일쿨러용 온도제어 설계법을 제안한다. 제안된 방법은 냉동사이클이 선형 1차계, PI 제어기를 포함한 냉동사이클의 폐루프 제어계가 2차계로
표현되어 그 동특성이 2차계의 특성 파라미터에 의해 지배되는 원리를 이용한다. 2차계의 특성 파라미터 항에 포함된 PI 게인은 주어진 설계사양과 ITAE
최적 평가함수를 적용함으로써 확정적(deterministic)인 방법으로 용이하게 구해진다.(10) 제안된 설계법은 시뮬레이션과 실험을 통해 그 타당성이 검증된다. 또한 본 논문에서는 부동작 시간의 영향, 무시 가능한 부동작 시간 범위, 제어대상의
파라미터 불확실성에 대한 제어기의 강인성에 대해서도 상세히 검토하였다.
2. 전달함수 모델링과 PI 제어기 설계
2.1 압축기와 EEV 전달함수 모델
Fig. 1은 오일쿨러 시스템의 주된 구성 요소인 냉동사이클의 모식도이다. 본 연구에서는 냉동사이클의 네 가지 구성 요소 가운데 압축기와 EEV를 제어대상으로
하였다. 제어량은 오일출구온도와 과열도, 조작량은 압축기 회전수와 EEV 개도(opening angle), 조작기로는 인버터(inverter)와 EEV
드라이브(drive)를 각각 사용하였다. 증발기는 오일탱크 내에 장착하였고, 열부하를 대신하여 전기히터를 사용하였다.
Fig. 1. Conceptual diagram of an refrigeration cycle.
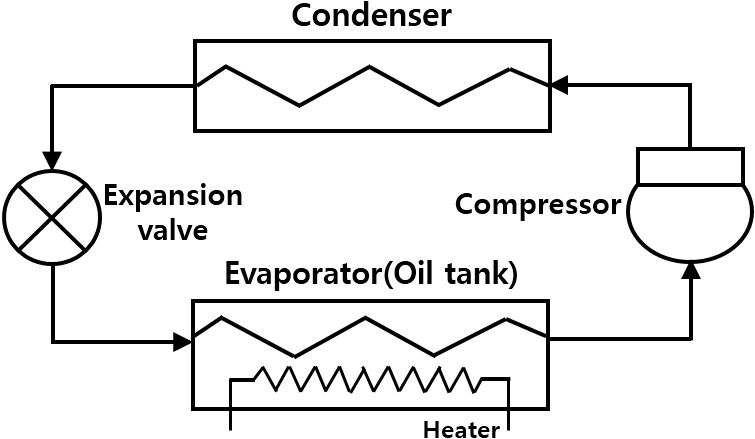
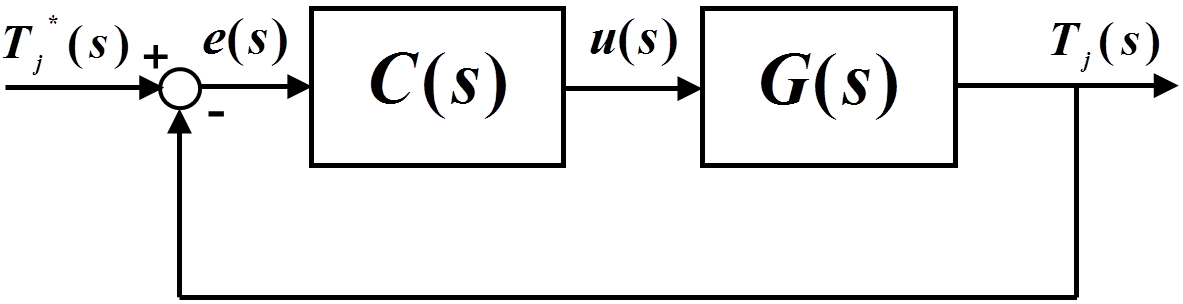
Fig. 2는 PI 제어기 C
j(s) (j=1, 2)로 압축기의 회전수 또는 EEV 개도를 가변시켜 오일출구온도와 과열도 T
j(s) (j=1, 2)를 제어하기 위한 오일쿨러 시스템의 피드백제어계의 블록선도이다.
Fig. 2. Block diagram of a closed-loop control system.
오일쿨러용 가변속 압축기의 전달함수 G
1(s)는 압축기 회전수에 상응하는 인버터 주파수 지령 변화에 대한 오일출구온도 변화를 실험적으로 구하였다. 전달함수는
식(1)과 같이 무시 가능한 짧은 부동작 시간을 갖는 1차계로 나타났다. EEV의 경우에도 압축기와 동일하게 섭동법으로 구한 전달함수 G
2(s)는
식(2)와 같다.
2.2 최적 PI 제어기 설계
식(1), 식(2)에서 압축기 및 EEV의 전달함수는 시정수가 매우 크고, 부동작 시간은 이에 비해 매우 짧다. 시정수가 클 경우, 실제 제어장치의 제어주기 또한 길게
설정된다. 따라서 PID(Proportional, Integral, Derivative)의 D제어기 영향은 상대적으로 작아지게 된다. 본 연구에서는
식(3)의 PI 로직만을 사용하여 제어기를 설계한다.
한편, 부동작 시간은 시정수에 비해 상대적으로 매우 짧기 때문에 무시할 수 있는 것으로 가정한다. 결국
Fig. 2의 PI 폐루프 제어시스템은 영점(zero)을 갖는 2차계로, 압축기의 경우
식(4-1), EEV의 경우
식(4-2)와 같이 표현된다. 이 때, 영점 는 PI 게인들의 비로써 이다. 2차계의 평가함수 ITAE의 최적화 조건인
식(5)를 만족하는 PI 게인은
식(4-1),
식(4-2)의 분모와 최적화 기준을 만족하는 특성다항식
식(5)를 각각 비교함으로써
식(6),
식(7)과 같이 구해진다.
여기서 ζ와 ω
n은 2차계 표준형의 특성값인 고유진동수와 감쇄비이다. 2차계 표준형에서 퍼센트오버슈트 M
p, 정착시간 t
s의 근사값은
식(8),
식(9)와 같이 ζ와 ω
n의 함수로 표현된다.
식(5)에서 ζ값이 고정되었으므로
식(6)의 좌변 값도 정해지게 되며, 결국 PI 제어기의 게인 K
p, K
i는
식(6)과
식(7)에서 모두 ω
n만의 함수로 된다.
식(9)에서 정착시간 t
s가 설계사양으로 주어지면, ω
n의 값이 구해지므로 이를
식(6)과
식(7)에 대입하면 평가지표 ITAE로 최적화된 PI 게인 값이 확정적으로 구해진다. 이처럼
식(4-1)은 실제로 영점을 갖는 2차계이지만, 설계시에는 2차계 표준형으로 간주해 PI 게인을 우선 결정하였다. 따라서 다음 단계에서는 영점의 영향을 고려하여
구해진 PI 게인을 미세 조정하는 과정을 거친다.
table 1은 압축기측 설계사양을
, M
p [%] ≤ 10 으로 하여 2차계 표준형에서의 PI 게인을 구한 경우와, PZM(Pole-Zero Map; 극-영점도)을 참고하여 영점의 영향을
고려하여 게인을 미세 조정한 경우의 ω
n과 PI 게인들을 각각 나타낸다.
table 1에서 Case 1은 영점을 고려하지 않은 ω
n 미세 조정 전의 값, Case 2는 ω
n 미세 조정 후의 PI 게인 값들을 각각 나타낸다. 게인 미세 조정시 제어 성능 향상을 위해 게인을 무한히 크게 증가시킬 수는 없다. 특히 비례게인
K
p의 경우, 오일쿨러 시스템의 안정적인 운전 및 인버터의 특성을 고려하여 30 근방으로 그 값을 제한하였다.
Table 1. Designed PI gains for compressor’s control
|
Case
|
ωn |
Kp |
Ki
|
|
1
|
0.0246
|
28.6
|
1.00
|
|
2
|
0.0250
|
29.4
|
1.04
|
table 2는 압축기와 동일한 방법으로 설계된 EEV측의 ω
n과 PI 게인들을 나타낸다. Case 1과 Case 2의 의미는 압축기의 경우와 동일하며, 주어진 설계사양은 t
s [sec] ≤ 108 (=4τ
2), M
p [%] ≤ 10 으로 하였다.
Table 2. Designed PI gains for EEV’s control
|
Case
|
ωn |
Kp |
Ki
|
|
1
|
0.053
|
16.7
|
1.30
|
|
2
|
0.054
|
17.4
|
1.31
|
3. 시뮬레이션 결과 및 고찰
시뮬레이션에서는 제어기 설계 과정에서 무시한 부동작 시간의 영향을 우선 확인한다. 다음으로 최적 PI 제어기의 제어 성능과 모델의 불확실성 및 모델
특성 파라미터 변동에 대한 강인성을 검증한다. 시뮬레이션 결과는 지면상의 제약을 고려, 압축기 회전수 제어에 의한 오일출구온도 제어 결과만을 집중적으로
기술하고 고찰하였다.
Fig. 3은
식(1)에서 부동작 시간을 무시한 선형 1차계 모델로부터 구해진 PI 게인을 부동작 시간을 갖는 비선형 모델
식(1)과 부동작 시간을 무시한 1차계 모델에 각각 적용하여 얻은 제어 응답이다. 두 응답이 거의 일치하므로 본 논문에서 제안한 선형 근사 1차계 전달함수
모델을 사용하여 PI 제어기를 설계하여도 제어 성능에는 전혀 문제가 없음을 확인할 수 있었다.
Fig. 3. Indicial responses of a real system with dead time and a first order system.
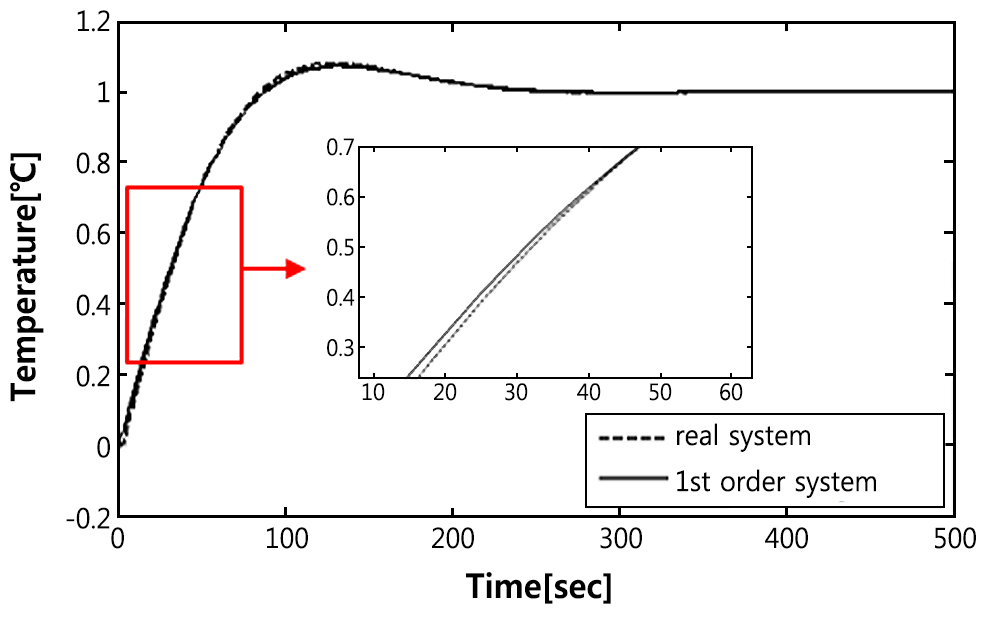
Fig. 4는 부동작 시간을 기존의 값(2 sec)과 기존 값 대비 2.5배, 4배 크기로 강제로 증가시킨 세 경우의 제어 응답을 나타낸다. 응답은 전반적으로
거의 유사하게 나타났다. 세부적으로는 부동작 시간이 길수록 초기 응답의 언더슈트와 최대 오버슈트가 커지고, 정착시간도 길어지는 경향을 보였다. 또한,
부동작 시간의 크기와 시정수 τ와의 상관성에 대한 시뮬레이션 결과, 부동작 시간이 시정수 τ의 0.095배 이하일 때는 부동작 시간을 무시하고 1차계로
근사하여 제어기를 설계하여도 설계사양을 충분히 만족시킬 수 있음을 확인하였다.
Fig. 4. Indicial responses according to change of dead time value.
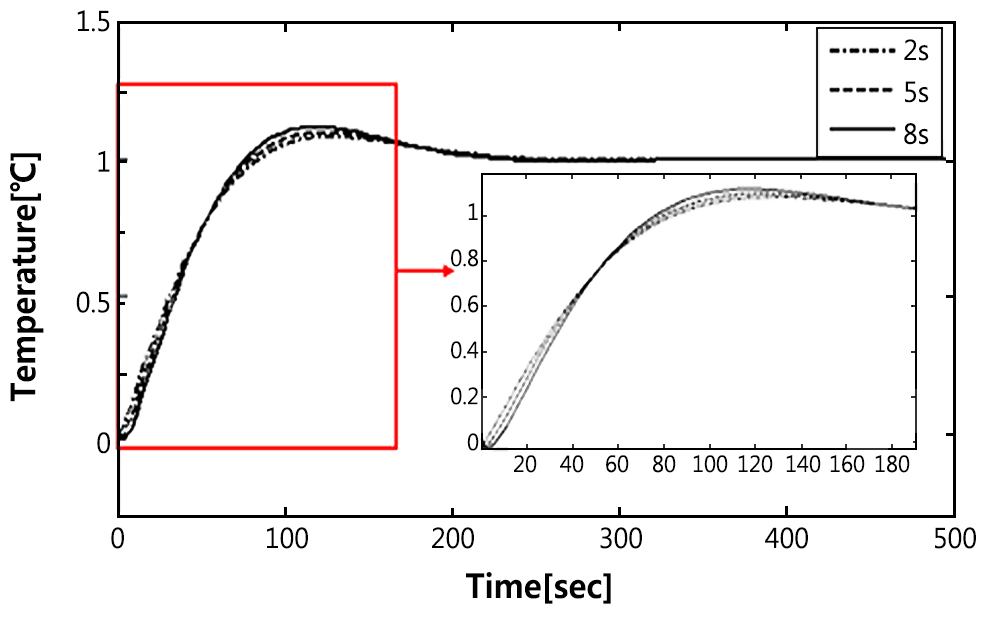
Fig. 5는 선형 1차계 모델을 대상으로 PI 제어기를 설계한 후, 영점의 영향을 고려하여 특성값 ω
n을 미세 조정한 경우와 조정하지 않은
table 1의 두 가지 게인에 대한 인디셜응답을 나타낸다. 두 경우에 있어서 PI 게인의 크기가 비슷하므로 인디셜응답 또한 유사하게 나타났다. 이는 K
p의 값이 실제 시스템 적용시 한계값인 30 근방으로 고정되어진 탓에 미세 조정할 수 있는 게인의 선택 범위가 좁아진 것에 기인한다.
Fig. 5. Indicial responses of case 1 and case 2 in Table 1.
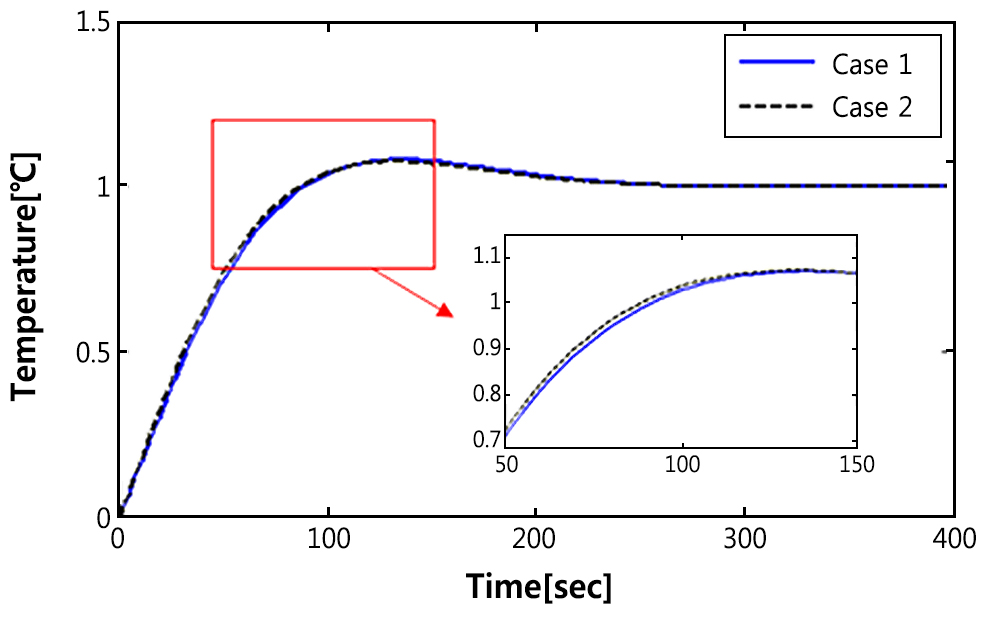
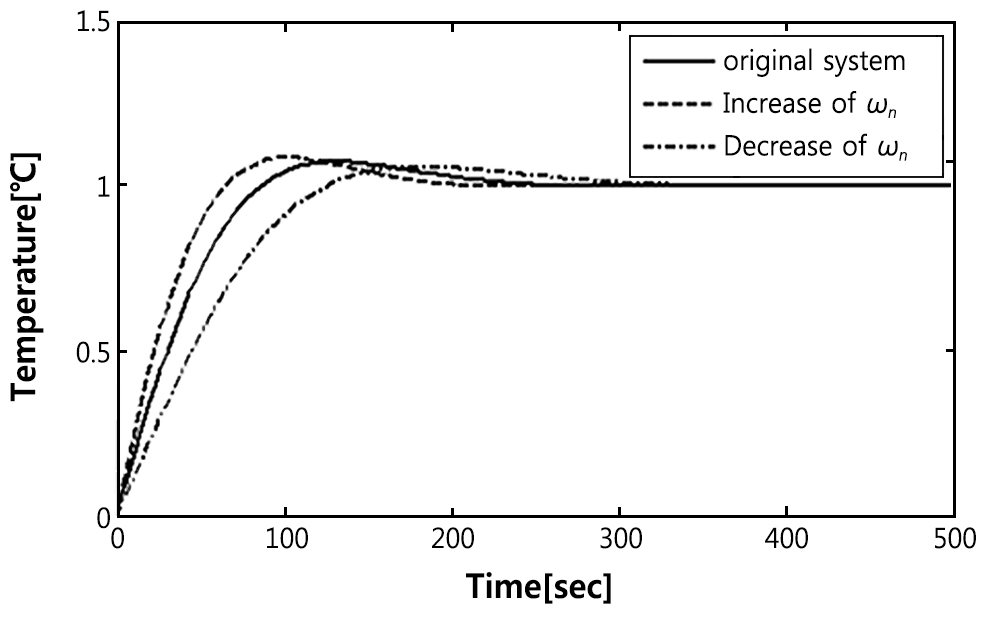
Fig. 6은 ω
n의 크기를 증·감시킨 경우의 인디셜응답을 보여준다.
식(7)에서 ω
n을 조정하면 K
p와 K
i값이 변하게 되므로 결국 과도응답 특성에 영향을 미친다. ω
n 증가시, 오버슈트가 미미하게 커지지만 응답속도도 빨라지므로 본 연구에서는 ω
n의 크기를 상향 미세 조정함으로써 PI 게인 값을 최종적으로 결정하였다.
Fig. 6. Indicial responses according to change of ωn.
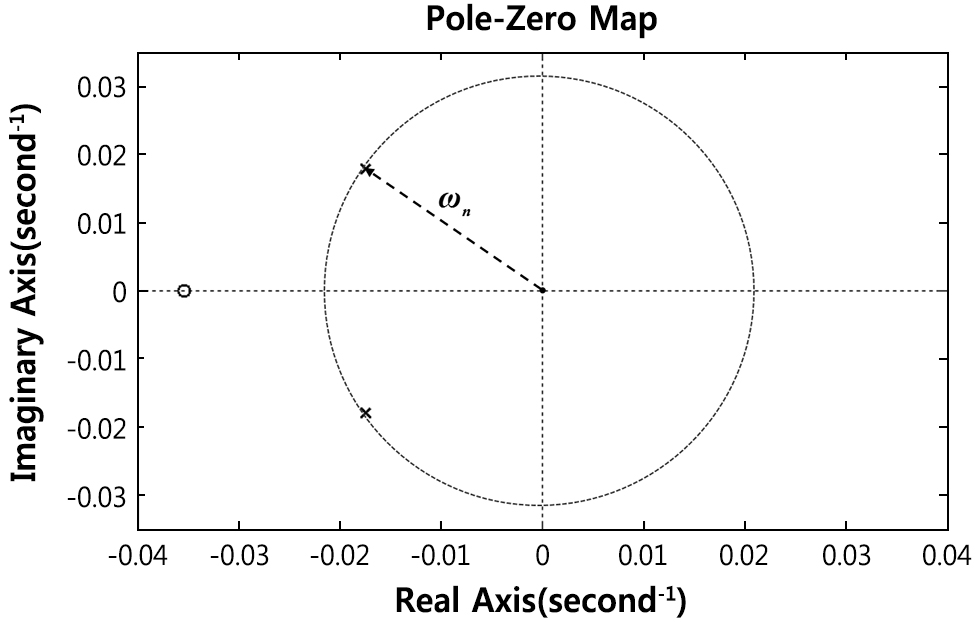
시스템의 극점 위치는 절대안정성을 판별하는 척도이며, 영점 또한 과도응답 특성에 영향을 준다. 제안하는 시스템은 실제로는 영점을 갖는 2차계이므로,
극점과 영점에 대한 안정성 고찰이 필요하다.
Fig. 7은 제안하는 시스템의 PZM을 나타낸다. 그림에서 점선은 주극점(“×”)을 반지름으로 하는 원을 나타내며, 영점(‘O’)은 이 원의 바깥쪽에 멀리
떨어져 위치하고 있다. 따라서 영점이 과도응답 특성에 미치는 영향은 작을 것으로 판단된다.
Fig. 7. Pole-zero map of the proposed PI control system.
또한, 오일쿨러 시스템의 냉동사이클은 본래 비선형성을 가지므로 제어시스템에 대한 안정성을 확인할 필요가 있다.
Fig. 8에 안정성 분석을 위한 오일출구온도 제어 시스템의 보드선도(Bode diagram)를 나타내었다. 보드선도에서 안정계의 조건은 게인여유(GM)와 위상여유(PM)가
각각 양의 값을 가지는 것이다. 선도에서 GM은 무한대이고 PM은 약 70°로, 프로세스 제어계의 상대안정성 요구를 만족시키고 있음을 확인하였다.
Fig. 8. Bode-plot of the proposed control system.
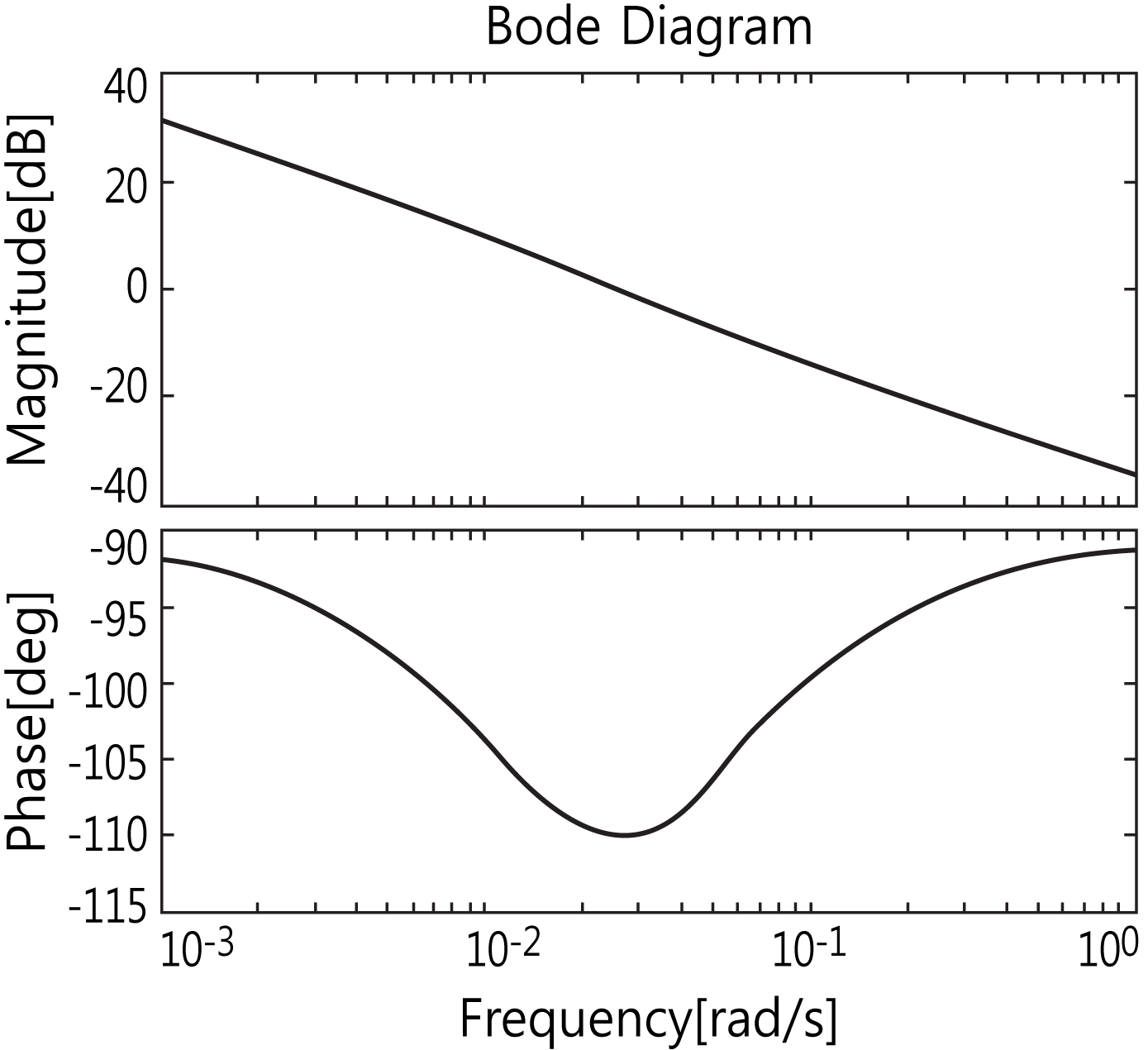
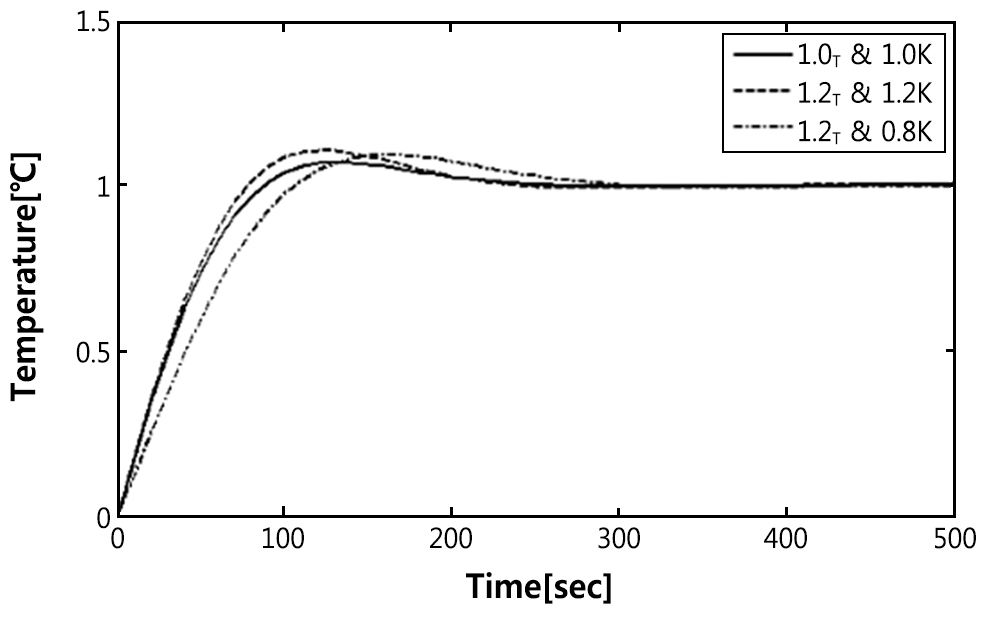
table 3은 시정수(τ)와 DC게인(K)을 각각 진치(standard)로부터 임의로 ±20% 변동시킨 네 가지 경우에 대한 정착시간과 오버슈트의 변화량을 보여준다.
프로세스 제어의 경우, 오버슈트 조건은 그다지 엄격하지 않으므로 정착시간 t
s에 대해서만 고찰한다.
Table 3. Dynamic characteristics in four cases
|
Condition
|
Mp |
ts
|
Change rate of ts[%]
|
|
Standard
|
7.2
|
210.9
|
-
|
|
0.8τ
|
0.8K
|
3.2
|
199.5
|
5.41
|
|
0.8τ
|
1.2K
|
10.7
|
164.5
|
22.00
|
|
1.2τ
|
0.8K
|
9.4
|
263.9
|
25.13
|
|
1.2τ
|
1.2K
|
4.3
|
210.3
|
0.28
|
Fig. 9는
table 3의 네 가지 조건 중 정착시간의 최대·최소 변동율을 보인 τ-K 두 조합과 표준(standard) 조건에서의 인디셜응답을 각각 나타낸 것이다. 1차계로
모델링된 제어대상의 특성 파라미터 τ와 K의 인위적인 변경(±20%)에도 제어계의 출력 응답 특성의 변화가 작으므로 제안한 오일쿨러 제어시스템은 파라미터
변동에 대해 강인함을 확인할 수 있다.
Fig. 9. Indicial response of the proposed PI controlsystem under parameters variation with ±20%.
4. 실험 결과 및 고찰
Fig. 10은 실제 실험장치인 오일쿨러 제어시스템을 보여준다. 공작기계를 대신한 열부하로는 전기히터(1.5 kW×2 EA)를 사용하였다. 제어장치로는 LabVIEW
시스템을 사용하였고, 오일출구온도와 과열도 측정을 위해 T-type 써모커플과 Pt-100을 사용하였다. 압축기의 조작기로는 “V/f = 일정” 타입의
인버터(6.1 kVA, 40-90 )와 EEV(ESX-18) 제어용으로는 스텝모터 드라이브(48- 500 )를 각각 사용하였다.
Fig. 10. Experimental equipment.

한편,
table 4는 실험 시스템의 사양,
table 5는 주요 실험 조건을 각각 나타낸다.
Table 4. Specifications of the test unit
|
Component
|
Note
|
|
Compressor
|
Rotary type, 3[HP], 30~120 Hz
|
|
Condenser
|
Air-cooled fin and tube type
|
|
Evaporator
|
Shell and tube type
|
|
Refrigerant
|
R-22
|
Table 5. Experimental conditions
|
Ambient
Ta[℃]
|
Target temperature[℃]
|
Heat load [kW]
|
|
Oil outlet To
|
Superheat Ts
|
|
27
|
25
|
11
|
0.79
|
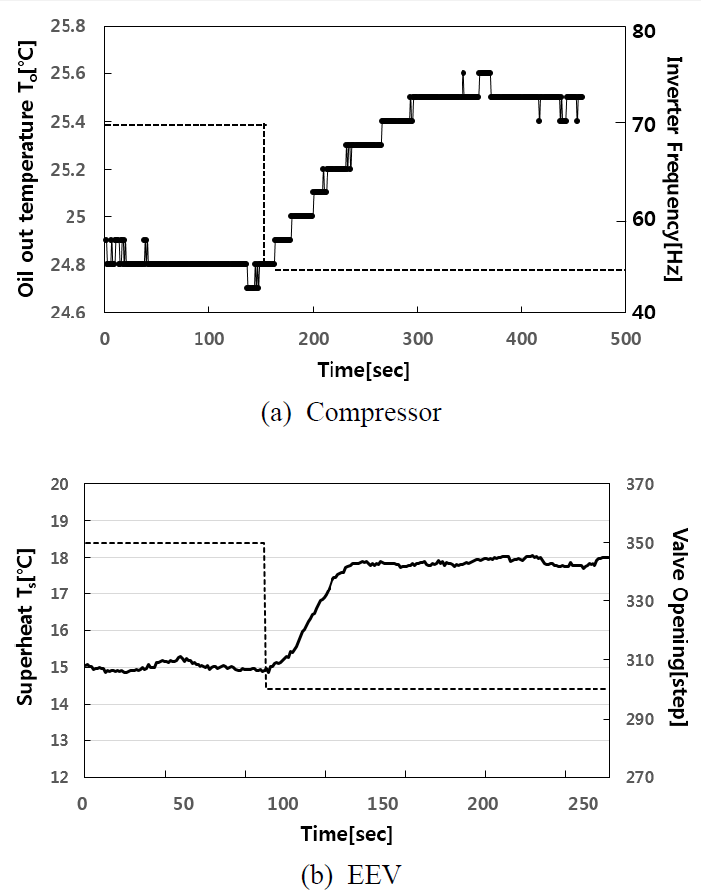
Fig. 11은 압축기와 EEV의 전달함수 모델링을 위해 섭동법으로 구한 동특성 실험 결과이다.
(a)는 인버터 주파수를 70 에서 50 로 가변했을 때(EEV 개도 350 고정)의 오일출구온도의 응답을 보여준다. 전형적인 1차계 응답 패턴이므로
이 데이터로부터 시정수 τ와 DC게인 K, 그리고 부동작 시간을 구하여 압축기의 전달함수 모델
식(1)이 얻어졌다.
Fig. 11(b)은 EEV 개도를 350 에서 300 으로 가변했을 때(압축기 60 고정) 과열도의 응답을 보여준다. 압축기 모델링과 동일한 방법으로 EEV의 전달함수
모델
식(2)를 얻었다.
Fig. 11. Modeling for a compressor and an EEV.
본 연구에서 설계한 PI 제어기(
table 1과
table 2의 Case 2)의 성능 평가를 위해 기동실험, 부하변동실험을 하였다.
특히 기동실험시 적분값의 포화로 인한 제어 성능 열화를 막기 위해 안티 와인드업(anti-wind up) 제어기를 부가적으로 설계하였다.
Fig. 12는 0.79 kW의 열부하를 인가한 상태에서 시스템 기동시 제어량인 오일출구온도와 조작량인 인버터 주파수, 그리고 과열도와 EEV 개도의 변화를 보여준다.
그림에서 가로 점선은 목표(설정)값을 의미한다. 오일출구온도의 경우, 정상상태오차가 ±0.04℃로 정밀하게 제어되고 있음을 알 수 있다. 과열도 제어의
경우, 200 sec 근방에서 인버터 주파수의 급격한 증가로 인한 간섭의 영향을 보이지만, 목표값인 11±0.4℃로 비교적 양호한 제어 결과를 보였다.
Fig. 12. Experimental results of starting up.
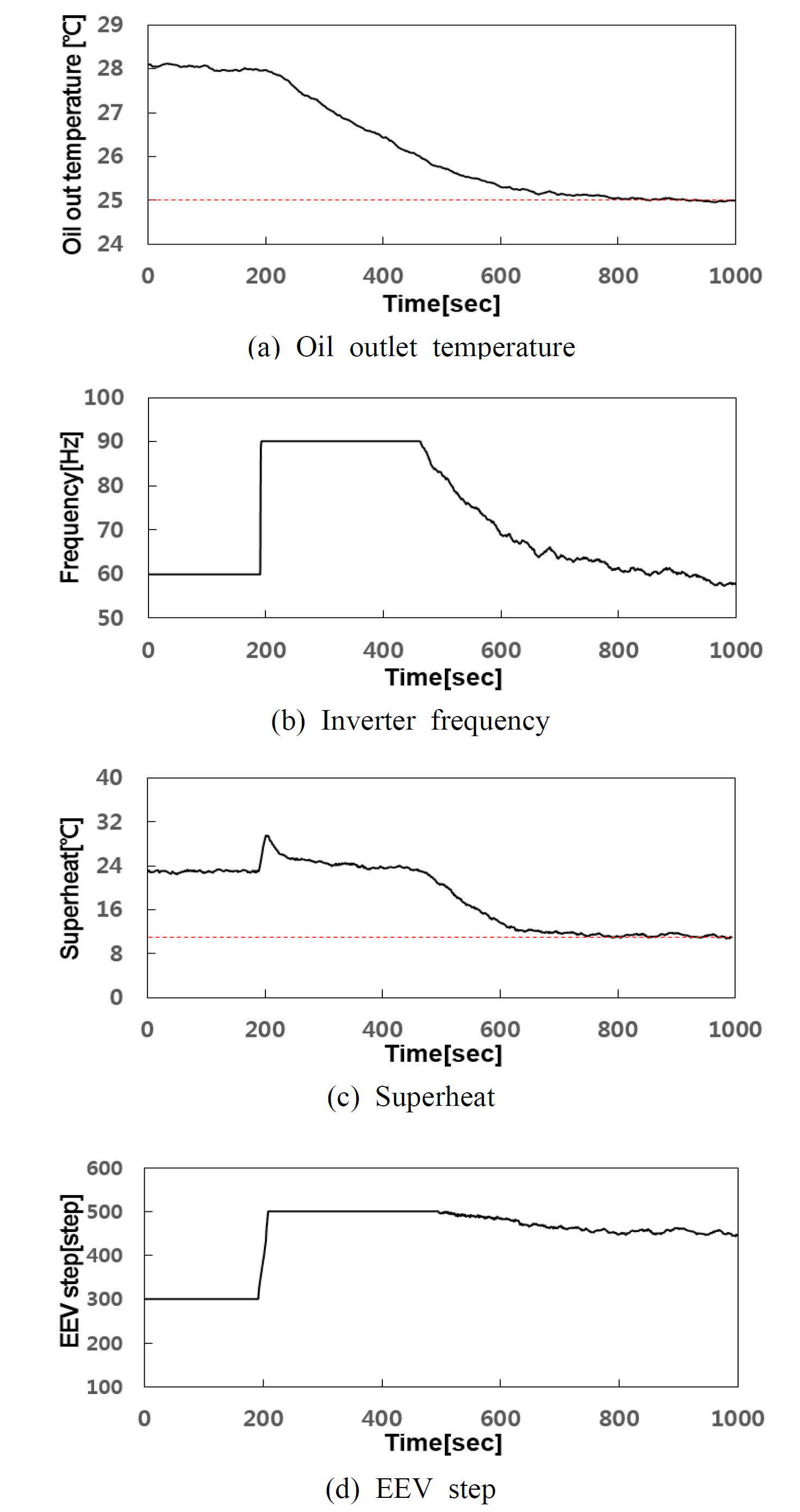
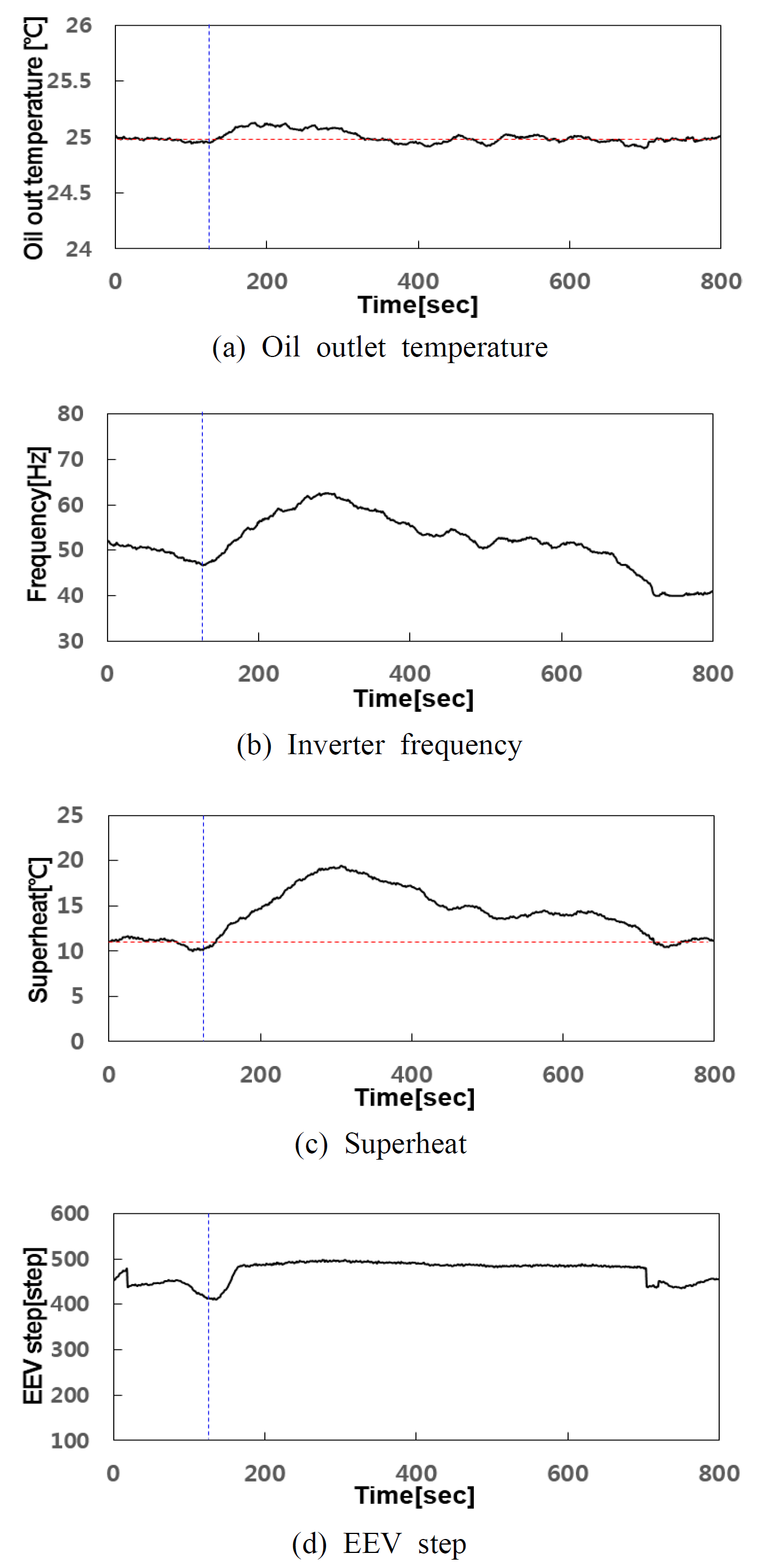
Fig. 13은 120 sec시점에 열부하를 0.58 kW에서 0.64 kW로 스텝 상으로 증가시킨 부하변동실험 경우의 각 제어량의 응답과 지령값의 변동을 보여준다.
부하변동실험은 기동실험과 동일한 조건 하에서 열부하만을 스텝 상으로 변경시켜 제어 성능을 확인하였다. 그림에서 세로 점선은 열부하를 변경한 시점을
나타낸다. 열부하 변동 하에서도 오일출구온도와 과열도의 정상상태오차는 ±0.04℃와 ±0.4℃로 나타나 양호한 제어 성능을 보였다.
Fig. 13. Experimental results of heat load variation.
5. 결 론
본 연구에서는 오일쿨러 시스템의 체계적인 최적 PI 제어기 설계법을 제안하였으며 주요 결론을 요약하면 다음과 같다.
(1) 부동작 시간이 짧은 오일쿨러와 같은 소형 냉동 시스템의 경우, 단순 선형 1차계 전달함수로 모델링 하고, PI 제어기만으로도 양호한 제어 성능
확보가 가능함을 확인하였다.
(2) ITAE 평가 기준을 적용한 최적 PI 제어기는 제어대상의 특성 파라미터가 ±20% 변동한 경우에도 제어계의 강인성 확보가 가능함을 시뮬레이션을
통해 입증하였다.
(3) 본 연구에서 설계한 PI 게인을 실제 오일쿨러 시스템에 적용하여 기동실험, 부하변동실험을 통해 양호한 제어 성능을 확인하였다. 오일출구온도와
과열도 제어의 경우 정상상태오차는 ±0.04℃, ±0.4℃로서 각각 고정도로 제어할 수 있었다.
본 논문에서 제안한 PI 제어기 설계법은 모델링의 간편성, 제어기 설계의 체계성과 용이성, 그리고 평가 기준을 적용한 최적 성능 확보가 가능하며 모델링
단계에서 발생하는 파라미터 불확실성에 대한 강인성도 확보되므로 향후 오일쿨러 시스템의 고정도, 고성능 제어기 설계법으로 유용하게 사용될 것으로 기대된다.
후 기
이 논문은 부경대학교 자율창의학술연구비(2016년)에 의하여 연구되었음.
References
Jung Y. M., Jeong S. K., Yang J. H., 2014, PI controller design of the refrigeration
system based on dynamic characteristic of the second order model, Journal of the Korean
Society for Power System Engineering, Vol. 18, No. 6, pp. 200-206

Jeong S. K., Hong K. H., 2013, Optimal PI controller design for refrigeration system
considering disturbance, Korean Journal of Air-Conditioning and Refrigeration Engineering,
Vol. 25, No. 2, pp. 85-93

Jeong S. K., Lee D. B., Yoon J. I., 2012, Comparison of system performances of hot-gas
bypass and compressor variable speed control of water coolers for machine tools, Korean
Journal of Air-Conditioning and Refrigeration Engineering, Vol. 24, No. 1, pp. 1-8

Shin Y. G., Yang H. C., Tae C. S., Jang C. Y., Cho S., Kim Y. K., 2005, A study on
PID tuning technique of a thermal environment chamber, Korean Journal of Air-Conditioning
and Refrigeration Engineering, Vol. 17, No. 11, pp. 1072-1079

Kim S. C., Hong D. S., Chung W. J., 2004, Temperature control for an oil cooler system
using PID control with fuzzy logic, Journal of the Korean Society of Manufacturing
Technology Engineers, Vol. 13, No. 4, pp. 87-94

Byun J. Y., Jeong S. K., 2010, Design of PI and feedforward controller for precise
temperature control of oil cooler system, Journal of the Korean Society for Power
System Engineering, Vol. 14, No. 6, pp. 89-95

Lee D. B., Jeong S. K., Jung Y. M., 2014, State equation modeling and the optimum
control of a variable-speed refrigeration system, Korean Journal of Air-Conditioning
and Refrigeration Engineering, Vol. 26, No. 12, pp. 579-587

Zheng F., Wang Q. G., 2001, Robust PI controller design for nonlinear systems via
fuzzy modeling approach, IEEE Trans. on Systems, Mans and Cybernetics, Vol. 31, No.
2, pp. 666-675

Li H., Jeong S. K., 2006, An empirical model for decoupling control of a variable
speed refrigeration system, Journal of the Korean Society for Power System Engineering,
Vol. 10, No. 3, pp. 81-87

Dort R. C., Bishop R. H., 1993, Modern Control Systems, pp. 176-185
Schurt L. C., Hermes C. J. L., Neto A. T., 2010, Assessment of the controlling envelope
of a model-based multivariable controller for vapour compression refrigeration systems,
Applied Thermal Engineering, Vol. 30, No. 13, pp. 1538-1546

Ekren O., Sahin S., Isler Y., 2010, Comparison of different controllers for variable
speed compressor and electronic expansion valve, International Journal of Refrigeration,
Vol. 33, No. 6, pp. 1161-1168
