Mobile QR Code QR CODE : Korean Journal of Air-Conditioning and Refrigeration Engineering

Korean Journal of Air-Conditioning and Refrigeration Engineering

ISO Journal TitleKorean J. Air-Cond. Refrig. Eng.

Open Access, Monthly

Open Access Monthly

ISSN : 1229-6422 (Print)
ISSN : 2465-7611 (Online)

Online Submission

Main Menu

Journal Search

[

Research article

]

Korean Journal of Air-Conditioning and Refrigeration Engineering

Korean J. Air-Cond. Refrig. Eng. Vol. 28, No. 12, p.467-476

ISSN (print) :

1229-6422

ISSN (online) :

2465-7611

Received : 18 July 2016Revised : 19 September 2016Accepted : 20 September 2016

DOI :

10.6110/KJACR.2016.28.12.467

Applicability of the Solar Irradiation Model in Preparation of Typical Weather Data Considering Domestic Climate Conditions

표준기상데이터 작성을 위한 국내 기후특성을 고려한 일사량 예측 모델 적합성 평가

Shim Ji-Soo (심지수) ¹ Song Doo-Sam (송두삼) ²^†

Dept. of Civil & Environmental System Engineering, Graduate School, Sungkyunkwan University, Suwon, 16419, Korea

(성균관대학교 대학원 건설환경시스템공학과)
School of Architectural, Civil and Environmental Engineering, Sungkyunkwan University, Suwon, 16419, Korea

(성균관대학교 건설환경공학부)

Correspondence to :

[†] Corresponding author, E-mail: dssong@skku.edu

License :

No part of this publication may be reproduced or distributed in any form or any means, or stored in a data base or retrieval system, without the prior permission of the publisher(www.sarek.or.kr).

Abstract

As the energy saving issues become one of the important global agenda, the building simulation method is generally used to predict the inside energy usage to establish the power-saving strategies. To foretell an accurate energy usage of a building, proper and typical weather data are needed. For this reason, typical weather data are fundamental in building energy simulations and among the meteorological factors, the solar irradiation is the most important element. Therefore, preparing solar irradiation is a basic factor. However, there are few places where the horizontal solar radiation in domestic weather stations can be measured, so the prediction of the solar radiation is needed to arrive at typical weather data. In this paper, four solar radiation prediction models were analyzed in terms of their applicability for domestic weather conditions. A total of 12 regions were analyzed to compare the differences of solar irradiation between measurements and the prediction results. The applicability of the solar irradiation prediction model for a certain region was determined by the comparisons. The results were that the Zhang and Huang model showed the highest accuracy (Rad 0.87~0.80) in most of the analyzed regions. The Kasten model which utilizes a simple regression equation exhibited the second-highest accuracy. The Angstrom-Prescott model is easily used, also by employing a plain regression equation Lastly, the Winslow model which is known for predicting global horizontal solar irradiation at any climate regions uses a daily integration equation and showed a low accuracy regarding the domestic climate conditions in Korea.

keywords

Solar collector, Flat plate collector, Vacuum insulation panel collector, Double-wall glazing collector

키워드

일사 예측 모델, 표준 기상데이터, 국내 기상조건

기호설명

I_g：Estimated solar radiation [W/m²]

I₀：Extraterrestrial horizontal irradiance [W/m²]

h：Solar altitude angle [degree]

z：Site elevation [m]

Φ：Site latitude [degree]

S：Sunshine duration [hr]

S₀：Duration of possible sunshine [hr]

CC：Cloud cover in tenth

T_n：dry-bulb temperature [℃]

$φ$ ：relative humidity [%]

Vw：Wind speed [m/s]

e_s(T)：Saturation vapor pressure at T [℃]

Prep：Precipitation [mm]

S_i：Model predictive value

M_i：Observed value

M_avr：Observed average value

n：Number of data

1. 서론

1.1 연구 배경

전 세계적으로 온실가스 감축이 중요한 문제로 거론되고 있으며 우리나라도 2030년까지 온실가스 배출 전망치(BAU, Business As Usual) 대비 37% 감축 이행을 약속하고,(1) 이를 위한 추진 계획을 작성하고 있다. 그 일환으로 국내 총 에너지 사용량의 21% 이상을 차지하는 건축물의 에너지 절감이 중요하게 거론되고 있다. 건물에너지 절감을 위한 다양한 기술들이 소개되고 있으며 그 효과를 검증하기 위해 다양한 시뮬레이션이 이루어지고 있다. 건물에너지 시뮬레이션을 통해 정확한 에너지 절감효과의 예측과 에너지 절감 방안을 작성하기 위해서는 해당 지역의 표준 기상 데이터 구비가 필요하다. 하지만 기상 관측 인프라의 한계로 건물에너지 시뮬레이션을 위한 표준 기상데이터는 세계적으로 한정된 지역에 제공이 되며,(2) 이 또한 실제 지역 기후 특성을 반영하지 못하는 한계를 가진다. 따라서 국내에 적합한 건물 에너지 절약 정책을 수립하기 위해서는 해당 지역의 기후 환경을 제대로 반영하는 표준 기상데이터의 작성이 반드시 필요하다.

1.2 연구 목적

표준 기상데이터는 다년간의 기상자료들을 바탕으로 해당 지역의 기상을 나타내는 1년 단위의 기상 데이터이다. 그러나 복잡한 작성 절차와 인식 부족으로 많은 연구자들이 단기 실측 기상자료나 평균값을 사용하고 있다. 표준 기상데이터 작성 시, 요구되는 여러 기후 요소 중 건물 에너지 소비에 가장 큰 영향을 미치는 요소는 건구온도와 일사량이다. 특히 일사량의 변화에 따라 여러 물리적인 요인들이 작용하며 건물 열 취득, 열 손실에 큰 영향을 준다.(3) 따라서 표준 기상데이터 작성에서 일사량의 정보는 반드시 필요하며 일사량 측정 또는 예측 과정과 직달․산란 일사 분리 과정이 매우 중요하다. 하지만 국내의 약 75개의 기상 측정지점 중 일사량 측정지점은 약 20곳에도 미치지 못하고 있다. 이러한 상황을 고려 할 때 표준 기상데이터 작성을 위해서는 불가피하게 국내의 일사량 미 측정 지역에 대한 일사량을 예측 과정이 필요하다. 국내에서 진행된 일사량 예측 관련 선행연구들은 국내의 대도시 지역을 위주로 단일 예측 모델을 통한 지역별 적합성을 판단하거나,(4,5,6) 단일 지역에 대한 다수의 모델을 통한 적합성 분석을 통한(7,8,9) 방식 등으로 진행되었다. 이러한 선행연구들은 일사량 예측에 있어 큰 영향을 미치는 국내의 미시 기후적 특징들과, 이에 따른 다양한 일사 모델들의 적합성이 적절하게 반영되지 못하였다는 한계를 나타낸다.

본 연구에서는 국내 지역별 적합한 표준 기상데이터 작성을 위해 일사량 측정데이터가 불비한 지역에 대한 일사량 예측 방법을 통해 일사량 데이터를 작성하고자 한다. 선행연구들의 한계점들을 보완하기 위하여 표준 기상데이터 작성에 주로 적용되는 동시에, 다양한 기상요소들을 적용하는 일사량 예측 모델을 선정하고 이들 모델들의 국내 기후 특징에 따른 적합성을 분석하였다. 분석은 현재 기상청에서 일사량을 측정하고 있는 지역에 대해 지리적, 기후적인 분류에서 대표성을 가지는 12개 지역에 대해 분석하였다. 대표 지역(12개 지역)에 대해 다양한 일사량 예측 모델을 적용하여 예측된 결과와 실제 측정치와 비교를 통해 각 일사량 예측 모델의 국내 적용성을 파악하고자 한다.

2. 연구 방법

2.1 국내 기후 특성을 고려한 분석 대상 지역 선정

표준 기상데이터 작성을 위한 일사량 예측 모델의 국내 적용성을 분석하기 위해 국내의 월별 누적일사량을 나타낸 기상자원지도(10)를 바탕으로 여름철과 겨울철의 일사량 차이가 560 MJ/㎡ 이상인 대표 지역 12곳을 분석대상 지역으로 선정하였다(Fig. 1 참조). 본 연구에서는 기상청(KMA)에서 제공하는 2010년의 종관기상관측자료를 이용하여 연구를 진행하였다.(11)

Fig. 1. The irradiance difference contour line and representative area.

../../Resources/sarek/KJACR.2016.28.12.467/fig1.png

2.2 일사량 예측 모델

일사량은 다양한 기상 요소들로 인해 천공에서 지표면 도달 시 반사, 산란 등에 의해 감소한다. 정확한 일사량 예측을 위해서 일사량에 영향을 미치는 기상 요소들의 상관관계에 관한 다양한 연구가 진행되었다.(12) 본 연구에서는 각기 다른 기상 요소들을 바탕으로 작성된 일사량 예측 모델을 통해(table 1 참조), 국내의 기후 특성별 일사량 예측 모델의 적용 가능성에 대해 분석하고자 하였다. 또한 표준기상데이터 작성에 국내외적으로 적극적으로 활용되는 일사량 예측 모델을 선정하였다. 검토하는 일사량 예측 모델은 Kasten model,(13) Zhang and Huang model,(14) Angstorm-Prescott model,(15) Winslow model(16) 등이다.

Table 1. Required Climate Conditions at Solar Irradiation Models

Model	CC	T_n	$φ$	S	Prep	TS	Note
Kasten(1983)	○					Hour
Zhang and Huang(2002)	○	○	○			Hour	Vw
Angstrom-Prescott				○		Day	S₀
Winslow(2001)		○	○		○	Day	S₀

*TS : Time step.

2.2.1 Kasten Model

ASHRAE에서 제공하는 전 지역의 IWEC 파일을 작동시키는데 사용되는 회귀식이다. 또한 건물에너지 시뮬레이션 프로그램인 EnergyPlus의 기상데이터 작성에 사용되었다.(17) table 1과 같이 Kasten 모델은 전운량 정보를 통해 지표면에 도달하는 일사량을 예측하는 모델로 이후 Muneer 모델 등이 Kasten 모델을 바탕으로 개발되었다.(13) 식(1)의 A, B, C, D는 지역계수로 각 지역의 운량 및 태양 고도를 바탕으로 산출 되는 계수이다.(18) 본 연구에서는 Kasten 모델에서 제공하는 대표 지역계수를 사용하였다.

(1)

I_{0} = (A \cdot s i n (h) - B)

$\frac{I_{g}}{I_{0}} = 1 - C \cdot (C C / 8)^{D}$

A=910, B=30, C=0.75, D=3.4

2.2.2 Zhang and Huang Model

중국 몇 개 지역의 일사량 실측데이터를 바탕으로 개발된 일사량 예측 모델로 현재 EnergyPlus의 중국 지역과 북아프리카 지역에 해당하는 기상데이터 작성에 사용되고 있다. Zhang and Huang 모델은 table 1과 같이 다양한 기후 요소(전운량, 상대습도, 운속, 건구온도, 풍속)의 관계식으로 이루어져 있다.(14) 전 세계 대부분의 지역에 대해 높은 정확성을 보인다. 식(2)의 c_0-5, d, k는 지역계수로, 베이징과 광저우의 실측값을 바탕으로 제안 되었다. 분석 대상 지역의 위도상 베이징(N 39.9°)과 광저우(N 23.1°)의 사이에 위치하기 때문에(19) 본 연구에서는 Zhang and Huang 모델에서 제공하는 대표 지역계수를 12지역에 동일하게 사용하였다.

(2)

w h e n I_{0} \geq 0,

$I_{g} = [I_{0} \cdot s i n (h) \cdot \{\begin{matrix} c_{0} + c_{1} \cdot (C C) + c_{2} \cdot (C C)^{2} + c_{3} \cdot (T_{n} - T_{n - 3}) + c_{4} \cdot φ + c_{5} \cdot V w \end{matrix}\} + d] / k$

$w h e n I_{0} < 0, I_{0} = 0$

$c_{0} = 0.5598, c_{1} = 0.4982, c_{2} = - 0.6762, c_{3} = 0.02842$

$c_{4} = - 0.00317, c_{5} = 0.014, d = - 17.853, k = 0.843 .$

2.2.3 Angstrom-Prescott Model

건축 이외의 타 분야에서 또한 자주 사용되는 전일사량 예측 모델이다. 대부분의 기상 지점에서 측정되는 가조시간-일조시간의 관계를 바탕으로 작성된 회기식이다(table 1 참조). 많은 기상정보가 필요하지 않고 단순하다는 장점으로 기상자료들을 수집하기 어려운 인도, 아프리카 등의 지역에서 많이 사용되는 방법이다. 본 연구에서 식(3)의 지역계수인 a와 b는 최미희 외(20)의 연구에서 제시된 국내의 지역별 계수를 사용하였다.

(3)

\frac{I_{g}}{I_{_{0}}} = a + b \cdot \frac{S}{S_{0}}

2.2.4 Winslow Model

전 지역에 해당하는 일사량을 예측하기 위해 고안된 식으로 일 최고, 최저 온도와 강수량만으로 일사 예측을 하기 위해 고안된 Bristow and Campbell 모델을 바탕으로 열대, 해안 지역, 습한 지역에 대한 기상요소를 보완하여 제시된 일사량 예측 모델이다. 이를 위해 대부분 지역에서 관측하는 기상요소들을 바탕으로 한 연구가 진행 되었다.(16)

(4)

I_{g} = τ_{c f} \cdot D \cdot [1 - β \cdot e_{s} (T_{m i n}) / e_{s} (T_{m a x})] \cdot I_{0}

τ_{c f}

는 청공상태의 대기투과율로 대기압(P/P_o), 지역 위도 변수(

τ_{o}

), 에어로졸에 관한 산란계수 (

τ_{a}

), 회귀계수(

τ_{v}

)의 관계로 구성된다. 여기서 T_mean은 연 평균온도이다. D는 지역별 가조시간에 의한 오류 발생을 줄이기 위해 고안된 계수이다. β는 회귀계수로써 일반적으로 1.041의 값을 사용한다.

(5)

τ_{c f} = (τ_{o} \cdot τ_{a} \cdot τ_{v})^{P / P_{O}}

$τ_{o} = 0.947 - (1.033 \cdot 10^{- 5}) (| ϕ |^{2.22})$

$f o r | ϕ | \leq 80 ° a n d τ_{o} = 0.774$

$τ_{a} = 1.0$

$τ_{v} = 0.9636 - 9.092 \cdot 10^{- 5} [(T_{m e a n} + 30)^{1.8232}]$

$P / P_{o} = [1 - (2.2569 \cdot 10^{- 5}) \cdot z]^{5.2553}$

$D = [1 - (S_{0} / 2 - π / 4)^{2} / 2 \cdot (S_{0} / 2)^{2}]^{- 1}$

3. 일사량 예측 모델 적합성 분석

3.1 오차 분석

일사량 예측 모델의 적합성을 분석하기 위해 일사량의 실측값과 예측값의 오차를 분석하였으며 이를 위해 MBE(Mean biased Error), CVRMSE(Coefficient of Variation of the Root Mean Square Error), 수정결정계수(Adjusted R Square)를 이용하였다.

MBE는 식(6)에서 알 수 있듯이 실측값과 예측값 차이의 합산으로, 실측값과 비교하여 예측값의 치우쳐진 정도를 나타내는 지표이다. 절대값이 작을수록 예측 모델의 정확도가 높다고 할 수 있다.(21)

(6)

M B E = \frac{\sum_{i = 1}^{n} (S_{i} - M_{i})}{\sum_{i = 1}^{n} M_{i}} \cdot 100

CVRMSE는 예측값과 실측값의 편차를 나타내며, 예측값의 불확실성과 오차의 범위 데이터의 분산 정도를 알 수 있는 지표이다. 즉, 예측값의 분산을 고려하여 예측값과 실측값간의 오차를 파악하는데 사용되는 방법으로 개별데이터가 준거집단의 평균으로부터 떨어진 정도를 파악할 수 있다.(21)

(7)

C V R M S E = \frac{\sqrt{\frac{\sum_{i = 1}^{n} (M_{i} - S_{i})^{2}}{n}}}{M_{a v r}} \cdot 100

수정결정계수(

R_{a d j}^{2}

)는 설명 변수들의 설명력의 정도를 나타내는 수치이다. 설명변수의 개수가 다른 경우에 변수의 설명력을 객관화하는데 사용되는 지표이다. 표본 크기가 많을수록 결정계수의 값이 커지는 경향이 있으므로, 본 연구에서는 수정결정계수를 사용하였다. 수정결정계수의 범위는

0 \leq R_{a d j}^{2} \leq 1

이며 값이 1에 가까워질수록 예측값의 설명력은 높다고 할 수 있다. 일반적으로 0.8 이상일 경우 설명력이 상당히 높은 것으로 0.5 이상인 경우에는 무난(acceptable)한 것으로 판단한다.

(8)

R^{2} = \frac{\sum_{i = 1}^{n} (M_{i} - S_{i})^{2}}{\sum_{i = 1}^{n} (M_{i} - S_{i})^{2} + \sum_{i = 1}^{n} (S_{i} - M_{i})^{2}}

$R_{a d j}^{2_{}} = 1 - (1 - R^{2}) \cdot \frac{n - 1}{n - k - 1}$

3.2 일사량 실측값과 예측값 오차 분석 결과

분석 대상 지역들을 바탕으로 일사량 예측 모델의 적합성에 대해서 분석을 하였다. 한국 기후표에 따른 기후 관측지점 번호순으로 작성되었으며,(22) 강릉과 제주의 경우 해당 지점의 기상 관측 데이터 부재로 인하여 위·경도와 기후 특성이 비슷한 북강릉과 고산으로 대체 하였다.

table 2는 오차 지표 분석 방법을 통한 지역․일사량예측 모델에 따른 적합도를 나타냈으며, Fig. 2는 실측된 일사량 데이터와 일사량 예측 모델별 예측데이터에 따른 최대·최소값(선형표현)과 총 365일(1일 적산)에 해당하는 데이터 중 상위 25%~75%(박스표현)가 집중되는 지점을 나타냈다. 전 지역의 실측 일사량 데이터의 분포는 평균적으로 0.82~30 MJ/m²로 하루 동안의 일사량 변동 폭이 큰 것으로 나타난다.

Table 2. Error Analysis between measurement and predicted solar radiation

Model Location		Kasten	Zhang and Huang	Angstorm- Prescott	Winslow
Daegwallyeong	MBE	-29.80	1.45	100.47	153.22
	CVRMSE	47.84	28.08	117.77	212.94
	$R_{a d}^{2}$	0.75	0.81	0.57	0.51
Chuncheon	MBE	-23.99	5.49	103.58	228
	CVRMSE	45.56	24.52	113.61	282.81
	$R_{a d}^{2}$	0.77	0.87	0.64	0.50
Gangneung	MBE	-24.3	0.5	118.85	216.82
	CVRMSE	44.22	27.89	130.72	275.83
	$R_{a d}^{2}$	0.77	0.81	0.60	0.35
Seoul	MBE	-17.27	14.81	106.24	235
	CVRMSE	42.05	28.54	118.60	289.83
	$R_{a d}^{2}$	0.78	0.86	0.61	0.46
Incheon	MBE	-23.71	1.69	108.09	165.63
	CVRMSE	39.91	25.36	120.53	222.99
	$R_{a d}^{2}$	0.80	0.84	0.60	0.33
Daejeon	MBE	-20.28	8.74	100.42	211.53
	CVRMSE	41.71	25.58	110.73	267.07
	$R_{a d}^{2}$	0.77	0.86	0.62	0.44
Daegu	MBE	-15.95	19.55	107	282.44
	CVRMSE	40.54	30.22	119.14	325.86
	$R_{a d}^{2}$	0.76	0.86	0.54	0.47
Gwangju	MBE	-18.80	8.66	107.69	196.3
	CVRMSE	41.93	26.42	119.03	222.99
	$R_{a d}^{2}$	0.79	0.85	0.62	0.33
Busan	MBE	-24.78	0.22	100.35	179.48
	CVRMSE	39.63	26.85	110.98	232.73
	$R_{a d}^{2}$	0.75	0.80	0.58	0.23
Mokpo	MBE	-22.77	5.92	113.06	82.76
	CVRMSE	44.70	27.05	120.99	145.83
	$R_{a d}^{2}$	0.77	0.82	0.67	0.22
Jeju	MBE	-24.69	5.42	90.31	151.44
	CVRMSE	42.82	31.32	98.61	197.72
	$R_{a d}^{2}$	0.78	0.80	0.79	0.3
Jinju	MBE	-19.44	5.88	90	197.64
	CVRMSE	38.62	24.85	99.9	252.11
	$R_{a d}^{2}$	0.80	0.85	0.62	0.41

Fig. 2. Comparison of measured irradiance and predicted irradiance.

../../Resources/sarek/KJACR.2016.28.12.467/fig2.png

전운량 데이터를 바탕으로 작성하는 Kasten 모델의 경우, 수정결정계수를 통한 정확성은 0.8(인천)~0.75(부산)로, 전체적인 모델의 설명력이 양호 한 것으로 판단된다. 실측값에 대한 예측값의 치우침 정도를 나타내는 MBE의 경우에 12지역에 있어서 음의 값을 나타낸다. 이는 전체적으로 실측값에 비해 낮게 예측이 되는 것을 의미한다. 이는 Fig. 2에서 또한 전 지역에 따른 최대·최소값을 비롯한 데이터의 집중도 또한 실측값에 대비하여 하향된 경향을 나타낸다. 하지만 전체적으로 MBE의 절대값이 15.95(대구)~29.80(대관령)을 나타냄으로써, 예측값과 실측값 사이의 관계가 유효하다고 판단 할 수 있다. 예측값의 분산을 고려한 Kasten 모델의 CVRMSE의 경우, 38.62(진주)~47.84(대관령)이며 예측값의 데이터가 실측값에 비교할 때, 양호하게 집중 되어 있는 편이다.

온도, 습도, 풍속 등의 다양한 기후 요소를 반영하는 Zhang and Huang 모델의 경우 국내 12개 모든 지역에 있어서 가장 우수한 정확성을 보였다. 수정결정계수 0.87(춘천)~0.80(제주)으로, 본 모델의 설명력은 매우 신뢰 할 수 있는 수준이다. Fig. 2의 실측값 데이터와 Zhang and Huang 모델 데이터를 비교 하였을 때, 최대·최소값에 있어서 본 모델이 실측값에 비해 상향된 추세를 보이고 있으며, 부산과 강릉의 경우 실측 데이터의 분포와 비슷한 경향을, 대구의 경우 실측값에 비해 상향된 경향을 보인다. 이는 MBE 측면에 있어서 동일하게 나타나는데, 0.22(부산)~19.55(대구)를 나타내며 부산(0.22), 강릉(0.5)의 경우에 예측값의 치우침 정도가 실측값과 거의 동일하다고 평가된다. CVRMSE의 측면에서 24.52(춘천)~31.32(제주)로, 예측값의 데이터의 분포가 우수하게 집중되어 있다.

일조시간과 가조시간의 관계로 작성되는 Angstrom- Prescott 모델의 경우, 예측 데이터의 변동 폭이 매우 적으며 일사량 실측값의 변동 폭을 적절하게 반영하지 못하는 경향을 보인다(Fig. 2 참조). 이는 1일 동안 균등하게 적용되는 가조시간의 기상 요소를 바탕으로 작성되었기 때문으로 판단된다. 수정결정계수는 0.79(제주)~0.54(대구)로, 일부 지역에 대한 설명력은 양호하지만 그 외의 지역에 있어서는 무난한 경향을 나타냈다. MBE의 값은 90(진주)~118.85(강릉)로 실측값에 대한 예측값의 반영이 적절하게 이루어지지 못하는 것으로 보인다. CVRMSE 또한 98.61(제주)~130.72(강릉)로, 실측값 대비 예측값의 분산 정도가 크다.

온도와 강수량(습기)의 관계를 통해 일사량 예측에 사용되는 Winslow 모델의 경우, Angstrom-Prescott 모델과 마찬가지로 실측 일사량 데이터의 반영이 적절하게 이루어지지 못하는 것으로 보인다(Fig. 2 참조). 본 모델의 수정결정계수는 0.51(대관령)~0.22(목포)를 보이며 신뢰하기 어려운 것으로 나타난다. MBE 또한 82.76(목포)~282.44(대구)로, 실측값에 대한 예측값의 치우침이 적합하게 반영되지 못하는 것으로 나타난다. Winslow 모델의 CVRMSE는 145.83(목포)~325.86(대구)이며, 전체적으로 국내 12지역에 대한 Winslow 모델의 적합성은 매우 낮은 것으로 나타난다.

3.3 일사량 예측 모델 별 적합성 분석

각 모델별 수정결정계수에 따라 우수한 설명력을 가진 지역과 열등한 지역을 선정하여 모델별 분석을 진행하였다. Fig. 3과 Fig. 4를 통하여 모델별 CVRMSE와 수정결정계수를 파악할 수 있다. 수정결정계수가 우수한 지역들은 Kasten 모델-인천(0.80), Zhang and Huang 모델-춘천(0.87), Angstrom-Prescott 모델-제주(0.79), Winslow 모델-대관령(0.51)이며, 열등한 지역으로는 Kasten 모델-부산(0.75), Zhang and Huang 모델-제주(0.80), Angstrom- Prescott 모델-대구(0.54), Winslow 모델-목포(0.22)로 분류 하였다.

Fig. 3. Plot of solar irradiation calculated Best goodness-of-fit sites.

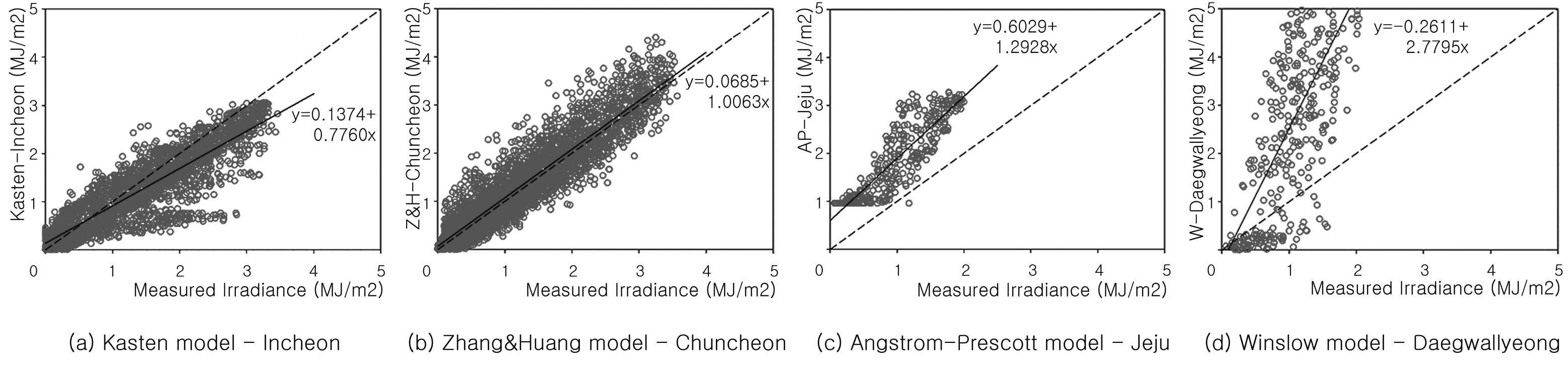
../../Resources/sarek/KJACR.2016.28.12.467/fig3.png

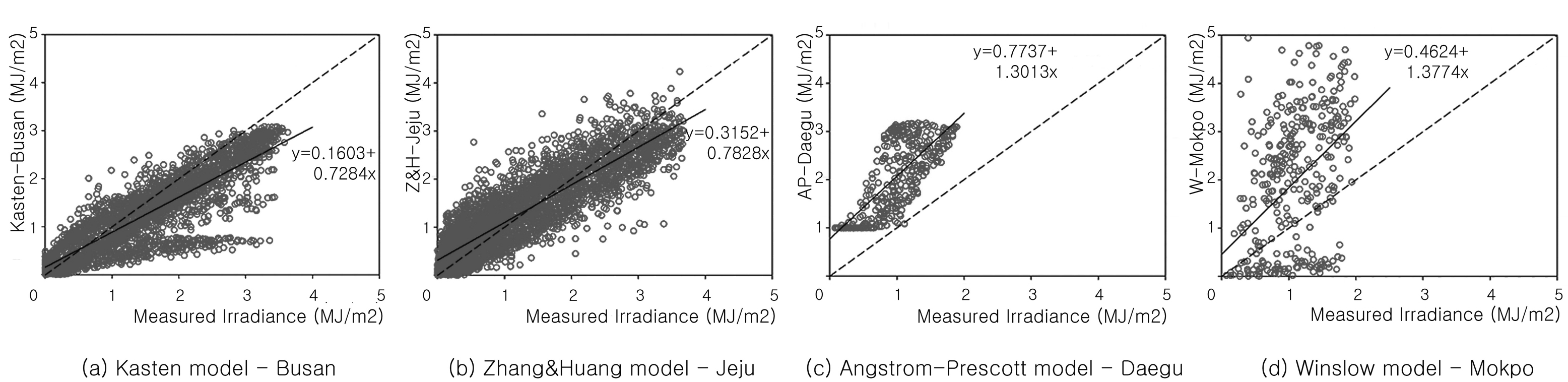
Fig. 4. Plot of solar irradiation calculated worst goodness-of-fit sites.

../../Resources/sarek/KJACR.2016.28.12.467/fig4.png

수정결정계수가 가장 우수한 Zhang and Huang 모델, 춘천의 경우 예측값의 패턴 기울기는 실측값과 거의 일치 하는 것으로 나타났으며, 데이터 일부는 실측값에 비하여 다소 상향되어 예측된 데이터들이 존재하는 것으로 보이나, 대부분은 패턴을 위주로 밀집되어 있는 형상을 띈다. Kasten 모델 인천의 경우, 예측값의 패턴 기울기가 실측값에 비하여 약간 낮게 나타나며, 개별 데이터의 대체로 밀집되어 있으나, 실측값이 높은 경우에 비교적 낮게 예측된 데이터들이 Zhang and Huang 모델과 비교를 하였을 때, 다수 존재하는 것으로 보이며 이는 본 모델의 설명력이 부족한 요소로 보인다. Angstrom- Prescott 모델 제주의 경우 예측값 패턴 기울기가 상향된 경향을 보인다. 즉, 대다수의 예측값이 실측값에 비하여 높게 예측됨을 의미한다. 또한 개별 데이터의 밀집 실측된 일사량이 1 MJ/m² 이하인 경우와 2 MJ/m²인 경우에 밀집되고, 이외의 개별데이터들이 퍼져 있는 분포를 보인다. Winslow 모델, 대관령의 경우 예측값 패턴 기울기가 매우 높은 분포를 나타냈다. 전체적인 개별 데이터의 분포가 패턴 기울기를 따라 넓게 퍼져있으며 실측 일사량이 1 MJ/m² 이하인 경우에 실측값에 비하여 낮게 예측이 되는 경향을 보인다(Fig. 3 참조).

각 모델 별 수정결정계수가 열등한 지역 중 Zhang and Huang 모델의 제주지역 수정결정계수가 4가지 모델 중 높은 것으로 나타났다. 실측된 일사량이 낮은 구간(약 0~1.2 MJ/m²)에서 약간 높게 예측되고, 실측 일사량이 높은 구간(약 1.8 MJ/m²~)에서 약간 하향되어 예측 되는 경향을 보임으로써 전체적으로 예측값 패턴의 기울기가 비교적 하향된 경향을 보인다. 개별 데이터의 분포가 패턴을 중심으로 비교적 밀집 되어 있으나 일부 값이 작은 실측값일 경우, 비교적 높게 예측되며 높게 실측된 값일 경우 낮게 예측된 데이터들로 인하여, 데이터 분포의 폭이 패턴을 따라 다소 퍼져 있는 모습을 볼 수 있다. Kasten 모델 부산의 경우 역시 실측값에 비하여 예측값의 패턴 기울기가 낮게 나타났으며, 이는 동일 모델의 인천 지역보다 실측된 일사량 전반에 걸쳐 낮게 예측되는 개별 데이터의 수가 증가한 것이 원인이다. Angstrom-Prescott 모델, 대구의 경우 패턴의 기울기는 동일 모델의 제주의 것과 비슷하지만, 개별 데이터의 분포가 기울기 패턴을 중심으로 상당 부분 넓게 퍼져 있는 경향을 보인다. 이로 인하여 CVRMSE의 값이 증가 한다. Winslow 모델, 목포의 경우 Angstrom-Prescott 모델의 패턴 기울기와 근접하며 또한 Winslow 모델-대관령에 비하여 패턴 기울기가 실측값과 근접하나, 일사량 실측값이 낮을 경우 매우 높게 예측되거나, 실측값이 0~2 MJ/m²일 때, 매우 낮게 예측되어 전체적인 데이터의 분포가 밀집하지 못하고 광범위하게 퍼져있는 모습을 보인다. 이러한 분포에 따라, Angstrom-Prescott 모델의 대구와 비교 하였을 때, 수정결정계수의 설명력이 매우 낮아지는 것으로 파악 된다.

3.4 월별 일사량 오차 분석

일사량 예측 모델의 월별 정확성을 파악함으로써, 지역·기간에 따른 오차값 추이에 대해서 알아보고자 하였다. 이를 위하여 일사 실측값과 예측값의 오차-월별 적산을 방법을 적용하여 분석하였다.

오차율은 MBE 값과 유사한 의미를 나타낸다. 실측값과 예측값의 감산 방식을 통한 적산 방법이기 때문에, Fig. 5~Fig. 8에서 값이 0에 근접 할수록 일사량 실측값과 예측값이 동일함을 의미하며, 양의 값은 예측값이 실측값 보다 상향되어있음을 나타낸다. 모델별 전체적인 패턴의 형태와 우수·열등한 MBE 값을 가지는 지역을 중심으로 분석하였다. 더불어 각 지역 모델별 기상요소와의 상관관계 자세한 분석을 위하여 MBE 수치가 열등한 지역과 우수한 지역에 대한 피어슨 상관관계(Pearson correlation coefficient) 분석(23)을 진행하였다. 피어슨 상관계수는 변수들 간의 상관관계에 대한 강도를 측정 하는 것으로, 상관관계가

0 < r \leq + 1

이면 양의 상관,

- 1 \leq r < 0

이면 음의 상관, r = 0이면 무상관이라고 한다. 식(9)에서 x와 y는 변수이다.

Fig. 5. Kasten model-Monthly difference value.

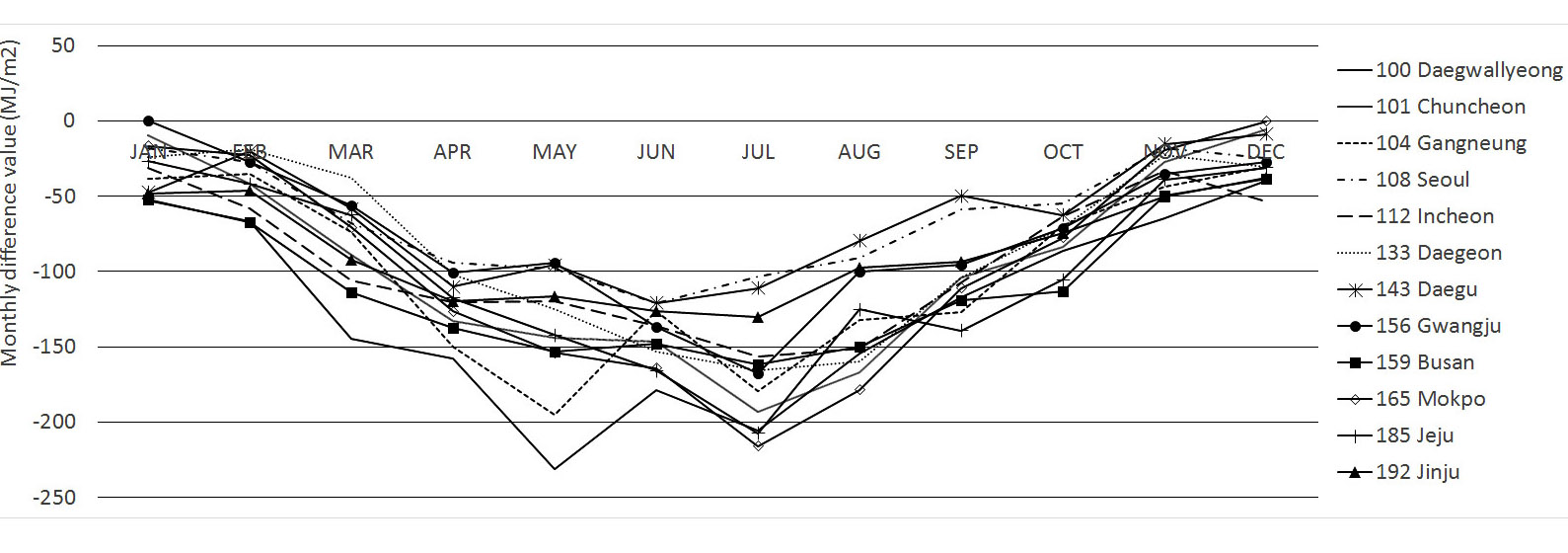
../../Resources/sarek/KJACR.2016.28.12.467/fig5.png

Fig. 6. Zhang and Huang model-Monthly difference value.

../../Resources/sarek/KJACR.2016.28.12.467/fig6.png

Fig. 7. Angstrom-Prescott model-Monthly difference value.

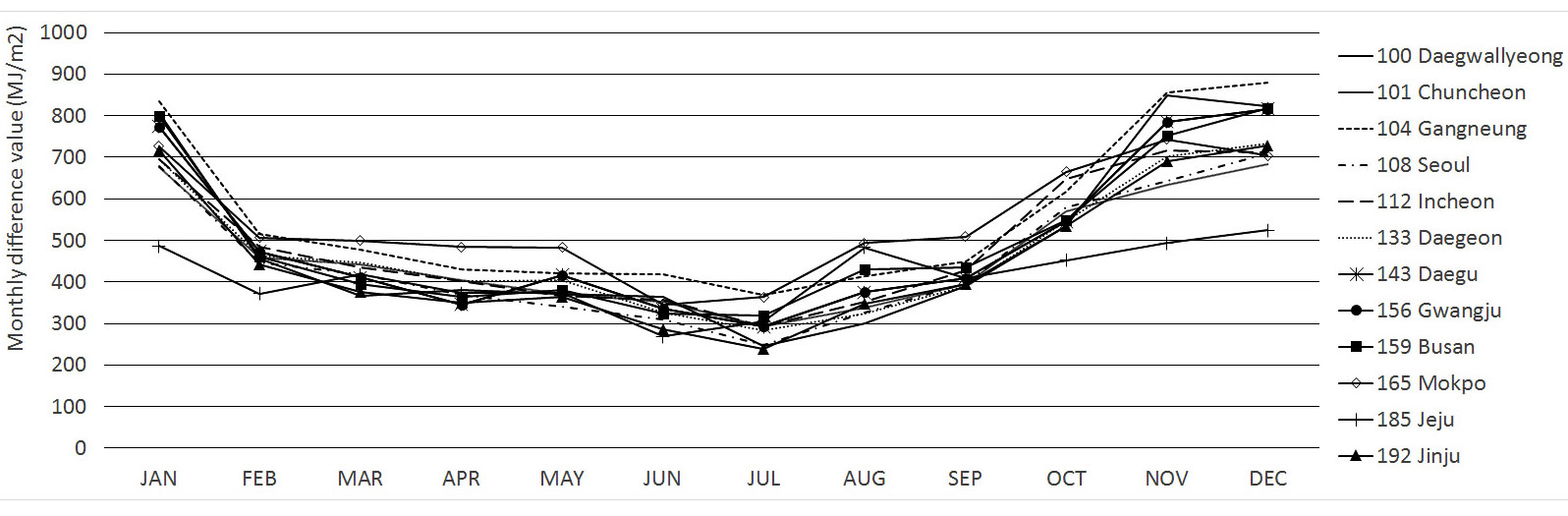
../../Resources/sarek/KJACR.2016.28.12.467/fig7.png

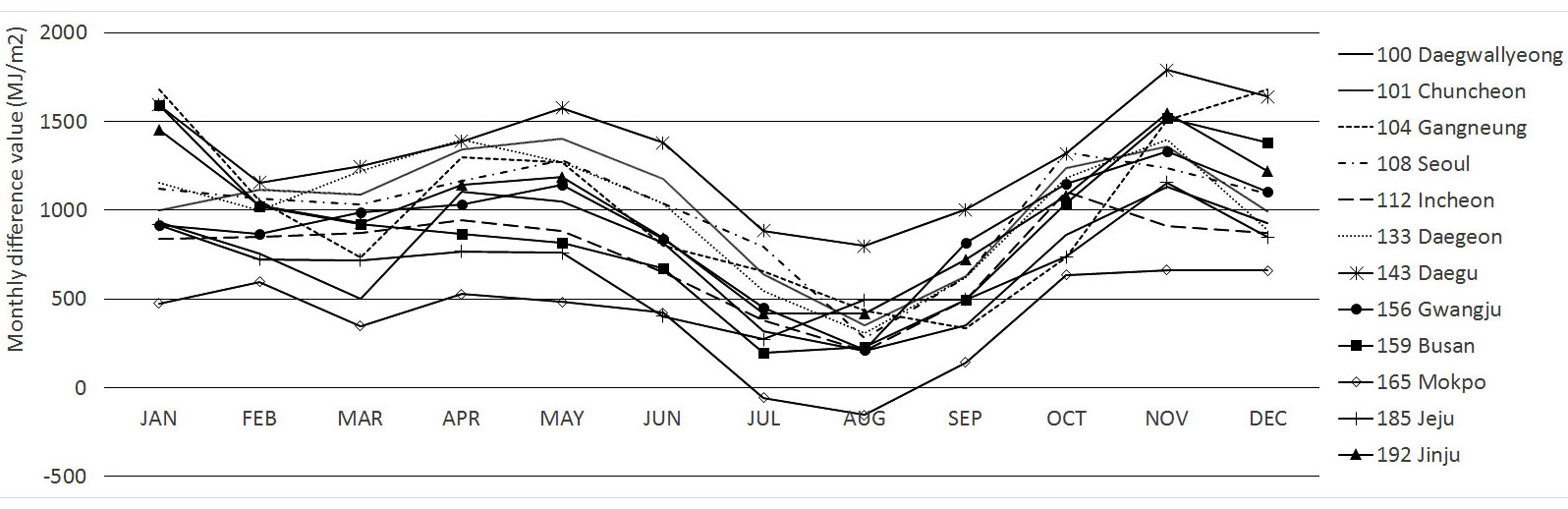
Fig. 8. Winslow model-Monthly difference value.

../../Resources/sarek/KJACR.2016.28.12.467/fig8.png

(9)

r = \frac{n (\sum_{}^{} x y) - (\sum_{}^{} x) (\sum_{}^{} y)}{\sqrt{[n \sum_{}^{} x^{2} - {(\sum_{}^{} x)}^{2}] [n \sum_{}^{} y^{2} - {(\sum_{}^{} y)}^{2}]}}

3.4.1 Kasten Model

Kasten 모델의 12지역 모두 예측값이 실측값에 비해 낮은 패턴을 보이며, 전 지역의 월별 오차 적산값은 0.42~-231.06 MJ/m²로 크지 않은 오차를 보인다. 11월에서 1월, 겨울 기간의 예측값이 실측값과 유사한 경향을 보인다. Kasten 모델에서 열등한 MBE 값을 보이는 대관령의 경우, 예측값과 실측값의 오차 정도가 타 지역에 비하여 크며, 특히 오차 적산값 -231.06 MJ/m²으로 5월에 오차값이 크게 나타난다. MBE 값이 우수한 대구의 경우, 2월과 11월, 12월의 오차값이 작으며, 1월과 9월에는 오차값이 약 50 MJ/m² 미만으로 전 지역의 오차 패턴과는 차이를 보인다. MBE 값이 열등한 대관령과 우수한 대구의 경우를 바탕으로 Kasten 모델의 예측된 일사량의 오차값과 기상요소간의 관계를 분석하였다. 실측·예측 오차값은 태양의 평균 고도각(대관령 : -0.954, 대구 : -0.908)과 크게 음의 상관관계로 관련이 있는 것으로 나타났다. 평균 운량 또한 대관령 : -0.621, 대구 : -0.688로 어느 정도 관계를 가지는 것으로 나타났다. 즉, Kasten 모델의 일사량 예측에 있어 오차값을 증가시키는 원인은 주로 고도각과 크게 관련 있으며, 운량의 영향은 부수적으로 미치는 것으로 보인다. 이러한 경향은 월별 오차 분석의 경향과도 일치 하는 것으로 나타난다.

3.4.2 Zhang and Huang Model

전반적으로 실측값과 예측값이 차이가 150 MJ/m² 이하로, 오차 폭이 크지 않다. 대부분 지역이 1~2월과 10월~12월 달의 오차율이 크지 않은 것으로 나타났다. 12개 지역이 일관된 오차 패턴이 아닌, 다양한 패턴을 보이는데, 이러한 패턴은 Zhang and Huang 모델 작성 시 다양한 기상 요소와 더불어 풍속과 같이 변동의 폭이 큰 기상 요소에 의한 것이라고 판단된다. MBE가 우수하게 나타난 부산의 경우에 겨울철에는 예측값이 실측값에 비해 높게 예측되며 여름철에는 반대로 낮게 예측된다. MBE가 열등한 것으로 나타난 대구의 경우에는 전체적으로 예측값이 실측값에 비하여 높게 예측되며, 1월의 경우에는 실측값과 유사하지만 그 외의 달에는 전체적으로 오차 범위가 증가 하는 경향을 보이며 특히 6월의 경우에 오차값이 146.52 MJ/m²로 크게 증가한다.

지역적 분석을 위해 Zhang and Huang 모델에서 이용하는 기상요소(고도각, 운량, 온도차, 습도, 풍속)와 일사량 실측․예측 오차값 간의 분석을 진행하였다. 고도각의 평균값에 있어서 부산 : -0.528, 대구 0.941의 상관관계를 나타냈으며, 평균 운량 부산 : -0.215, 대구 : 0.687, 온도 평균 부산 : 0.028, 대구 : 0.206, 평균 습도 부산 : -0.706, 대구 : 0.308, 풍속평균 부산 : 0.401 대구 : 0.172의 관계를 가지는 것으로 나타났다. Zhang and Huang 모델의 일사량 오차값이 작을수록, 평균 습도, 평균 풍속과 오차값간의 관계가 높은 것으로 나타났으며, 오차값이 커질수록, 고도각과 평균 운량과의 관계가 높아짐을 알 수 있다. 결과적으로, Zhang and Huang 모델의 지역계수를 고려 할 때, 습도와 풍속에 관한 상관관계에 대한 고려가 필요하다.

3.4.3 Angstrom-Prescott Model

12개 지역 모두 실측값에 비교하여 예측값이 높게 예측되며 오차값은 200~900 MJ/m² 이하로 큰 변동 폭을 나타낸다. 대부분 지역에 대한 예측 패턴이 유사하게 나타나며, 여름철에 비하여 겨울철인 11~1월 사이의 오차값이 매우 커지는 경향을 보인다. MBE가 우수한 진주의 경우, 가을과 겨울철 오차값이 증가하고 여름철의 오차값이 감소하는 패턴을 보여, 본 모델의 오차값 패턴의 대표적인 특징을 반영한다. 반면 MBE가 열등한 강릉의 경우에는, 11월과 1월 사이의 오차값이 타 지역에 비하여 크게 증가를 하는 경향을 보이며, 7월의 오차값이 겨울에 비하여 감소하지만 전 지역 중 높은 오차폭을 보인다.

자세한 분석을 위하여 Angstrom-Prescott 모델의 실측·예측 오차값과 본 모델에서 사용한 기상 요소인 가조시간과 일조시간의 관계에 대하여 분석하였다. MBE가 우수한 진주의 경우 평균 일조시간 0.533, 평균 가조시간 -0.918로 나타났으며, MBE가 열등한 강릉의 경우 평균 일조시간 0.357, 평균 가조시간 -0.888로 나타났다. 상관관계를 볼 때, Angstrom-Prescott 모델의 오차율과 크게 관계를 가지는 기상요소는 가조시간으로 판단되며, 오차율과 일조 시간간의 관계는 부수적인 것으로 나타났다.

3.4.4 Winslow Model

Winslow 모델의 경우, 11월~1월, 5월에 높은 오차값을, 7월과 8월에 오차값이 낮아지는 특징을 보이며, 이는 대부분 지역의 오차 패턴에 있어서 유사한 특징을 나타낸다. 겨울철의 오차값은 약 800~1500 MJ/m², 여름철에는 500 MJ/m²의 차이를 보이며, 계절에 따른 오차 변동 폭이 크다. 전 지역의 오차값은 MBE가 우수한 목포와 열등한 대구 사이에 해당한다. 목포의 경우에는 7월의 실측값과 예측값의 오차는 약 56 MJ/m²으로 타지역에 비하여 상당히 오차폭이 적은 것으로 나타나며, 10~12월 사이의 실측값과 예측값의 패턴은 유사 하다. 대부분의 오차 변동 특징과 다르게 1월의 오차값이 500 MJ/m²으로 작게 나타난다. 대구의 경우, 오차값이 1789.5 MJ/m²으로 전반적으로 가장 큰 오차값을 보이며, 이는 11월에 가장 크게 나타난다. Winslow 모델의 경우, 위·경도, 연평균온도와 더불어 가조시수와 상대습도, 일 최대·최저 온도의 자료를 사용하나, 위도 경도 연평균온도의 경우 1년 내내 동일한 값을 사용함으로, 이외의 기후 정보들과 오차율관계에 대하여 분석을 진행하였다. Winslow 모델 중 MBE 결과가 우수하게 나타난 목포의 경우에, 일별 최고 온도 평균 -0.725, 일별 최저 온도 평균 -0.776, 일별 상대습도 평균 -0.946 가조시수 평균 -0.603으로 일사량 오차율과 전반적으로 음의 상관관계를 형성하는 것으로 나타났다. MBE가 열등한 대구의 경우, 일별 최고 온도 평균 -0.601, 일별 최저 온도 평균 -0.686, 일별 상대 습도 평균 -0.869, 가조시수 평균 -0.509의 관계를 가지고 있는 것으로 나타났다. 전 지역 모두 최고․최저 온도, 상대 습도가 일사량 오차율과 높은 상관관계를 가지고 있는 것으로 나타났으며, 이에 대한 보완이 필요하다고 판단된다.

4. 결 론

본 연구에서는 국내 75개 지역의 적절한 기후 상황을 반영한 표준 기상데이터 작성을 목적으로 진행되었다. 일사량 미측정 지역에 대한 일사량 예측을 위해 선행적으로 12개 대표 지역에 대하여 국내외에서 활발하게 사용되며, 일사량에 영향을 미치는 다양한 기상 요소들을 반영하여 일사량 예측 모델의 정확성을 판단하기 위해서 Kasten Model, Zhang and Huang Model, Angstorm-Prescott Model, Winslow Model 4개의 일사량 예측 모델을 적용하여 그 적합성을 분석하였다.

(1) 국내 12개 전 지역에 걸쳐 모델 예측값의 정확성이 가장 높은 모델은 Zhang and Huang 모델로 수정결정계수는 0.87~0.8로 나타났다. 국내의 모든 지역의 일사량 예측 정확성 측면에서는 Zhang and Huang의 모델이 우수 한 것으로 나타났으며, 국내에 적합한 일사량 예측 모델이라고 판단된다.

(2) 기상 요소로 전운량만을 고려하는 회귀식의 특징과 회귀식의 단순성을 고려 할 때, Kasten 모델 이용 역시 우수하다고 판단된다.

(3) 일별 일사량 적산 예측 방법인 Angstorm-Presscott 모델은 단순한 회귀식을 통해 다양한 분야에서 사용될 수 있으나, 정확성 측면에 있어서 국내 전 지역에 사용하기에는 한계가 있다.

(4) Winslow 모델은 일별 일사량 적산 예측 방식이나, 회귀식이 매우 복잡함과 동시에 국내 전 지역의 정확도 측면에서 매우 낮은 신뢰도를 보이고 있기 때문에, 표준 기상데이터 사용에 있어 부적합하다.

(5) 국내 기후 특징에 따른 일사량 적합성이 높다고 평가 된 Zhang and Huang 모델과 Kasten 모델의 경우, 전반적으로 일사량 예측 정확성이 높지만, 여름철에 비하여 겨울철 일사량 예측의 정확성이 높은 것으로 나타났다.

(6) 일사량 예측 모델의 정확성을 높이기 위한 연구로써, 오차값과 기상요소 간의 관계를 Pearson 상관관계를 통하여 분석함으로, 오차 발생 요인을 알아보고자 하였다. Kasten 모델의 경우, 오차율과 고도각간의 강한 관계를 보이며, Zhang and Huang 모델의 경우에는 습도와 풍속이 큰 영향을 미치는 것으로 나타났다. Angstrom-Prescott 모델의 경우에는 일조시간 보다는 가조시간이 오차값과 강한 관계를 가지는 것으로 나타났으며 Winslow 모델의 최고·최저온도와 상대 습도가 오차값에 큰 영향을 미치는 것으로 나타났다.

(7) 일사량 예측 모델의 정확성을 높이기 위해서는, 월별 오차 분석과 오차값과 기상요소간의 상관관계를 바탕으로 한 지역계수 보완에 관하여 추후 연구가 필요 할 것으로 판단된다.

후 기

본 연구는 국토교통부 국토교통기술촉진연구사업의 연구비지원(16CTAP-C098308-02)에 의해 수행되었습니다.

References

Ministry of Trade , 2015, Korean quantified emission limitation & reduction objects, Industry and Energy

Younes S., Muneer T., 2006, Improvements in solar radiation models based on cloud data, Building Service Engineering Research Technology, Vol. 27, No. 1, pp. 41-54

Li D. H. W., Lam J. C., 2000, Solar heat gain factors and the implications to building designs in subtropical regions, Energy and buildings, Vol. 32, No. 1, pp. 47-55

Yoo H. C., Lee K. H., Park S. H., 2008, Analysis of Data and Calculation of Global Solar Radiation based on Cloud Data for Major Cities in Korea, Journal of the Korean Solar Energy Society, Vol. 28, No. 4, pp. 17-24

Jo D. K., Kang Y. H., 2010, A Study on the Solar Radiation Estimation of 16 Areas in Korea Using Cloud Cover, The Korean Solar Energy Society, Vol. 30, No. 4, pp. 15-21

Jo D. K., Yoon C. Y., Kim K. D., Kang Y. H., 2012, A Study on the Estimating Direct Normal Insolation Using Horizontal Global Insolation for Solar Thermal Generation System Installation in Korea, The Korean Solar Energy Society, Vol. 32, No. 3, pp. 77-87

Kim K. H., Oh J. K. W., 2014, Impact by Estimation Error of Hourly Horizontal Global Solar Radiation Models on Building Energy Performance Analysis, Journal of the Korea Institute of Ecological Architecture and Environment, Vol. 14, No. 2, pp. 3-10

Yoon K. C., Jeon J. U., Kim K. S., 2012, Comparative Analysis of Measurements and Total Solar Irradiance Models on Inclined Surface for Building Solar Energy Prediction, The Korean Solar Energy Society, Vol. 32, No. 6, pp. 44-52

Kim T. H., Yoo S. Y., Han K. H., Kang H. C., Yoon H. I., 2013, A Study on Solar Radiation Model for Prediction of Solar Insolation, The Korean Society of Mechanical Engineers, pp. 670-675

2010, National Institute of Meteorological Research, Weather Resource Maps.

2010, Korea Meteorological Administration, Synoptic Climate Data.

Reno M. J., Hansen C. W., Stein J. S., 2012, Global Horizontal Irradiance Clear Sky Models : Implementation and Analysis, Sandia Report

Kasten F., Czeplak G., 1980, Solar and terrestrial radiation dependent on the amount and type of cloud, Solar Energy, Vol. 24, No. 2, pp. 177-189

Zhang Q., Huang J., Lang S., 2002, Development of Typical Year Weather Data for Chinese Locations, ASHRAE Transactions, Vol. 108, pp. 1063-1075

Angstrom A., 1924, Solar and Terrestrial Radiation, Quaterly Journal of the Royal Meteorological Society, Vol. 50, No. 210, pp. 121-126

Winslow J. C., Hunt E. R., Piper S. T., 2001, A globally applicable model of daily solar irradiance estimated from air temperature and precipitation data, Ecological Modelling, Vol. 143, No. 3, pp. 227-243

Copper J. K., Sproul A. B., 2010, Influence of Solar Radiation Models in the Calibration of Building Simulation Models, Solar 2010, the 48th AuSES Annual Conference

Yoo H. C., Lee K. H., Park S. H., 2008, Analysis of Data and Calculation of Global Solar Radiation based on Cloud Data for Major Cities in Korea, Journal of The Korean Solar Energy Society, Vol. 28, No. 4, pp. 17-24

Kim K. H., Oh J. K. W., Jeong W. S., 2016, Study on Solar Radiation Models in South Korea for Improving Office Building Energy Performance Analysis, Sustainability, Vol. 8, No. 6, pp. 589

Choi M. H., Yoon J. I., Jung Y. R., Moon K. H., 2010, Performance of Angstrom-Prescott Coefficients under Different Time Scales in Estimating Daily Solar Radiation in South Korea, Korean Journal of Agricultural and Forest Meteorology, Vol. 12, No. 4, pp. 232-237

Fabrizio E., Monetti V., 2015, Methodologies and Advancements in the Calibration of Building Energy Models, Energies, Vol. 8, No. 4, pp. 2548-2574

2011, Korea Meteorological Administration, Climatological normals of Korea 1981~2010

Kim B. W., Kang I. J., Han K. B., 2010, Insolation Modelling using Climate and Geo-Spatial Elements, Journal of the Korean Society for Geo-Spatial Information System, Vol. 18, No. 4, pp. 79-86

KJACRKorean Journal ofAir-Conditioning and Refrigeration Engineering

Korean Journal of Air-Conditioning and Refrigeration Engineering

ISO Journal TitleKorean J. Air-Cond. Refrig. Eng.

Journal Search

Journal XML

Journal Information

Applicability of the Solar Irradiation Model in Preparation of Typical Weather Data Considering Domestic Climate Conditions

Abstract

keywords

키워드

기호설명

1. 서론

1.1 연구 배경

1.2 연구 목적

2. 연구 방법

2.1 국내 기후 특성을 고려한 분석 대상 지역 선정

Fig. 1. The irradiance difference contour line and representative area.

2.2 일사량 예측 모델

Table 1. Required Climate Conditions at Solar Irradiation Models

2.2.1 Kasten Model

(1)

2.2.2 Zhang and Huang Model

(2)

2.2.3 Angstrom-Prescott Model

(3)

2.2.4 Winslow Model

(4)

(5)

3. 일사량 예측 모델 적합성 분석

3.1 오차 분석

(6)

(7)

(8)

3.2 일사량 실측값과 예측값 오차 분석 결과

Table 2. Error Analysis between measurement and predicted solar radiation

Fig. 2. Comparison of measured irradiance and predicted irradiance.

3.3 일사량 예측 모델 별 적합성 분석

Fig. 3. Plot of solar irradiation calculated Best goodness-of-fit sites.

Fig. 4. Plot of solar irradiation calculated worst goodness-of-fit sites.

3.4 월별 일사량 오차 분석

Fig. 5. Kasten model-Monthly difference value.

Fig. 6. Zhang and Huang model-Monthly difference value.

Fig. 7. Angstrom-Prescott model-Monthly difference value.

Fig. 8. Winslow model-Monthly difference value.

(9)

3.4.1 Kasten Model

3.4.2 Zhang and Huang Model

3.4.3 Angstrom-Prescott Model

3.4.4 Winslow Model

4. 결 론

후 기

References

Article Information (continued)

keywords

키워드

KJACRKorean Journal of
Air-Conditioning and Refrigeration Engineering