The bandgap reference (BGR) is commonly used to provide a stable reference voltage in analog and mixedsignal systems [1-3]. To ensure the performance of these systems over an operating temperature range, the reference voltage with low temperature drift is required.
To achieve a stable reference voltage with respect to temperature variations, traditional BGR linearly combines a voltage with positive temperature coefficient (TC) and a voltage with negative TC induced from a bandgap core, which is called linear TC compensation [4,5]. The negative TC voltage is derived from the emitter-base voltage ($V_{EB}$) of bipolar junction transistor (BJT), and the positive TC voltage is generated from the difference between two $V_{EB}$s (△$V_{EB}$) with different TCs. While the △$V_{EB}$ has only proportional-to-absolute-temperature (PTAT) term, the $V_{EB}$ contains complementary-to-absolute-temperature (CTAT) term and an additional nonlinear term which causes the curvature error [6]. This introduces a constraint on achieving a lower TC for the reference voltage.
To address this issue, recent studies have proposed BGRs with segmented curvature compensation [7,8]. This method initially divides the operating temperature range into several segments. In each segment, a term complementary to the $V_{EB}$ is added to generate curvature-compensated voltage. By using the curvaturecompensated voltage, the BGR generates the reference voltage with low TC. However, it requires additional current sources to generate those terms for each segments, which degrades the power efficiency.
Given this challenge, this paper proposes a sub-BGR with the segmented curvature compensation method that reuses the bandgap core to enhance power efficiency. The sub-BGR divides the temperature range into several segments by utilizing a CTAT voltage and PTAT current inherent in the bandgap core. Furthermore, the resistor within the bandgap core is used to generate the curvaturecompensated voltage. Therefore, the proposed BGR improves overall power and area efficiency.
This paper is organized as follows: Section II introduces the basic principle of segmented curvature compensation. Then, Section III explains the method of proposed low power segmented curvature compensation. Section IV discusses the overall circuit implementation of the proposed sub-BGR. The measurement setup and measurement results are presented in Section V. Finally, Section VI summarizes the conclusions.

 Fig. 1 shows the principle of the segmented curvature compensation. $V_{NTC}$ and $V_{PTC}$ denotes the negative and positive TC voltages derived from the $V_{EB}$ and △$V_{EB}$, respectively. $V_{REF1}$ is the voltage obtained by the linear combination of $V_{NTC}$ and $V_{PTC}$. Since $V_{REF1}$ exhibits the concave downward curvature due to $V_{EB}$ [6], the segmented curvature compensation is applied to suppress the curvature error.
Fig. 2 illustrates the temperature segmentation and segment-wise correction of the segmented curvature compensation. The temperature segmentation is performed first, dividing $V_{REF1}$ into same voltage intervals △V. The divided curves become temperature segments, and temperature range of each segments are used for the following segment-wise correction. Since $V_{REF1}$ exhibits a concave downward curvature, the middle segment has the highest voltage level. To equalize the voltage levels of the other segments with that of the middle segment, multiple of △V appropriate for each segments are added toVREF1 as shown in Fig. 2. These multiple of △V, added to each segments, are referred to as correction voltages. Finally, by combining VREF1 with the correction voltages, the curvaturecompensated reference voltage, $V_{REF}$, can be obtained.

  The proposed sub-BGR employs segmented curvature compensation by reusing a bandgap core. Fig. 3 shows the concept of segmented curvature compensation in the proposed sub-BGR. The temperature segmentation is implemented using PTAT current, $I_{BIAS}$, and CTAT voltage, $V_{C,1}$, from the bandgap core. The $V_{C,1}$ is compared with PTAT voltages, $V_{P,1-P,8}$, which are generated by the mirrored IBIAS flowing through a resistor, RP. The $V_{C,1}$ intersects with$V_{P,1-P,8}$, creating temperature cross points, $T_{1-8}$. As a results, the entire temperature range is divided into several segments by $T_{1-8}$.
The segment-wise correction is implemented by using tapped voltages, $V_{C,1-C,8}$, from resistor, RC. The details of the segment-wise correction in the proposed sub-BGR are illustrated in Fig. 4. By using the segments divided by temperature segmentation, the correction voltages are determined as multiples of the voltage intervals, △V, as mentioned in Section II (Fig. 4(a)). To enable the reuse of RC in the bandgap core, the proposed sub-BGR matches the voltage levels of all segments to the lowest voltage level of $V_{REF1}$. This is achieved by subtracting the correction voltages from $V_{C,1}$, resulting in $V_{C,1-C,8}$ from RC. Then, the multiplexer (MUX) selects $V_{C,i}$ (i = 1, 2, ..., 8) corresponding to each segment and outputs the selected segment-wise corrected CTAT voltage, $V_{CTAT,lin}$, as shown in Fig. 4(b). Consequently, in the proposed sub-BGR, the bandgap core is reused to provide the voltages utilized for both temperature segmentation and segment-wise correction, achieving high power and area efficiency.

 Fig. 5 presents the overall circuit diagram. The proposed sub-BGR consists of a bandgap core circuit, comparison block, analog MUX, and stacked self-cascode MOSFET (SCM). The bandgap core circuit generates all voltages required for segmented curvature compensation. The comparison block performs temperature segmentation and transfers the information of segmented temperature range to an analog MUX. With the information, the MUX outputs segment-wise corrected CTAT voltage, $V_{CTAT,lin}$, by multiplexing voltages in the bandgap core. Finally, the stacked SCM generates reference voltage by adding a PTAT voltage to the $V_{CTAT,lin}$. The details of circuit implementation will be discussed in this section.

1. Bandgap Core Circuit

 The bandgap core circuit produces temperaturedependent voltages, $V_{C,1}$ and $V_{P,1-P,8}$ for temperature segmentation and $V_{C,1-C,8}$ for segment-wise correction. The $V_{C,1}$ is the voltage copied from $V_{EB1}$ by amplifier A1. Since the voltage difference between $V_{C,1}$ and $V_{EB2}$ is applied to $R_C$, the bias current, $I_{BIAS}$, can be expressed as follows:

 where $V_T = kT/q$ is the thermal voltage exhibiting PTAT, N is the area ratio of $Q_2$ and $Q_1$, and is set to 8, considering both common centroid layout and size.With a current mirror $M_{P3}$ and a resistor string $R_{P,1-8}, V_{P,1-P,8}$ are expressed as

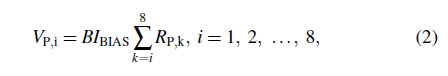
 where B is theW=L ratio of the pMOS current mirror from $M_{P1} (orM_{P2})$ to $M_{P3}$ and is set to 8, considering the tradeoff between power consumption and the size of the $R_2$. The $V_{C,1-C,8}$ utilized to segment-wise correction are generated by tapping voltages from the RC. $V_{C,1-C,8}$ can be expressed as

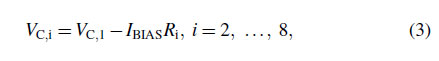
 where $R_i$ is the divided resistance between the points where $V_{C,1}$ and $V_{C,i}$ are tapped. The $I_{BIAS}R_i$ in Eq. (3) becomes the correction voltages mentioned in Section III.

2. Comparison Block and Analog MUX

 Fig. 5 also illustrates the comparison block and analog MUX. $V_{C,1}$ and $V_{P,1-P,8}$, generated from the bandgap core, are compared using comparators. As the $V_{C,1}$ intersects with $V_{P,1-P,8}$, creating temperature cross points, the comparator outputs, $D_{1-8}$, can provide the information about the segmented temperature range divided by these points. The $D_{1-8}$ is decoded to one-hot code, SEL<1:9>, which is used for the analog MUX to outputVC;i at corresponding segment, resulting $V_{CTAT,lin}$.
For the low power consumption, the proposed sub-BGR uses the large resistance of $R_C$ and $R_{P,i}$. However, the use of large resistance induces significant thermal noise to comparator input. This may cause the comparator output to change abruptly near the temperature cross points which degrades the TC. Therefore, a hysteresis comparator which is utilized in [8,9] is applied in the proposed BGR to ensure stable operation through hysteresis characteristic.

3. Stacked SCM

 The stacked SCM is applied [10] for linear TC compensation. The SCM structure composed of $M_t$ and $M_b$ is presented in Fig. 5. The SCM produces $V_{rmSCM}$, which exhibits PTAT characteristic dependent on the ratio of both the bias current and device size. The $V_{rmSCM}$ is expressed as

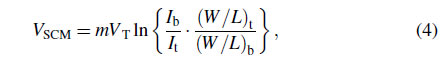
 where m is the subthreshold slope factor, I and W=L are the bias current and aspect ratio, respectively. Moreover, in the stacked SCM, four $V_{rmSCM}$s are stacked to achieve higher TC, whose absolute value is the same as TC of $V_{CTAT,lin}$, but with the opposite sign. Finally, the stacked PTAT voltage, $V_{PTAT,SCM}$, is added to the $V_{CTAT,lin}$ using a unity gain buffer, $A_2$, resulting $V_{REF}$. The $V_{REF}$ can be expressed as

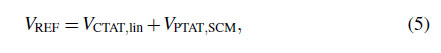
 and TC of $V_{REF}$ becomes

 where $TC_{VREF}$ is TC of $V_{REF}$ and $TC_{VREF1}$ is TC of $V_{REF1}$ which is the reference voltage without curvature compensation, as shown in Fig. 4(a). Since $V_{REF1}$ is divided into nine segments symmetrically arranged around the middle segment, $TC_{VREF}$ becomes five times lower than $TC_{VREF1}$.

  An on-chip test circuit [11] was applied to measure the reference voltage accurately, as shown in Fig. 6. An onchip output buffer is required for driving sufficient current. However, the reference voltage is measured with the offset of the output buffer, $V_{OS}$, added. To mitigate $V_{OS}$ from measured value, the alternate switch $S_{1-2}$ and external reference voltage are utilized. Firstly, the $V_{OS}$ can be calculated by measuring when the output buffer is connected to $V_{REF-IN}$. The $V_{OS}$ is expressed as

  where $V_{REF-IN}$ is external reference voltage, $V_{OUT-EXT}$ is measured voltage when the switch $S_1$ is off and $S_2$ is on. Then, the reference voltage is calculated by measuring the voltage when the output buffer is connected to BGR. Therefore, $V_{REF}$ is expressed as

  where $V_{OUT-BGR}$ is measured voltage when $S_1$ is on and $S_2$ is off. As a result, the accurate value of reference voltage is measured.
The on-chip test circuit is also utilized for trimming by controlling the voltage level of $V_{REF-IN}$. Basically, the VREF_IN was set to 1.2 V to suppress switch channel leakage. However, when $V_{REF-IN}$ becomes near 0 V at same condition, the off-state switch $S_2$ operates at subthreshold saturation region [12]. In that region, the channel leakage current exhibits an exponential dependence on temperature, with the rate of variation increasing as $V_{GS}$ increases. The channel leakage current flows into the stacked SCM and is added to $I_b$ in Eq. (4). At that time, a small change in $V_{GS}$ results in a nearly linear change in the PTAT characteristic of the $V_{rmSCM}$.
The proposed sub-BGR was fabricated by a 180 nm CMOS process, which occupies an active area of 0.21 mm$^2$. Fig. 7 shows the die photograph and layout details. TC of $V_{REF}$ is simulated from -40℃ to 120℃ as shown in Fig. 8. The VREF exhibits a variation of 1.36 mV over the entire temperature range, corresponding to a TC of 6.9 ppm/℃. The noise performance of the proposed sub-BGR is also simulated. The total integrated noise from 0.1 to 10 Hz is 49.4 mV, of which the noise of the bandgap core is 11.1 mV and the noise of the stacked SCM is 38.3 mV. 10 samples were measured from -40℃ to 120℃ to verify the TC of the proposed sub-BGR. Fig. 9(a) presents the measured untrimmed VREF. VREF was measured at 10℃ intervals to verify the operation of segmented curvature compensation. By applying 2-point trimming at -40℃ and room temperature, we obtained better performance, as shown in Fig. 9(b). The average TC of 10 samples of untrimmed VREF over the temperature range from -40℃ to 120℃ is 81.39 ppm/℃. After trimming, the average TC becomes 17.69 ppm/℃, with the best value of 9.9 ppm/℃. The 10 measured VREF at room temperature exhibits a mean value of 1.191 V and a standard deviation of 0.44 mV, indicating a 3σ inaccuracy of 1.12%.
Fig. 10(a) illustrates the line sensitivity of measured at room temperature. The reference voltage increases by 0.6 mV as the supply voltage rises from 1.5 V to 2 V, indicating an average line sensitivity of 0.05 %/V. In addition, Fig. 10(b) shows the power consumption of the proposed BGR under 1.8 V supply except for that of output buffer. It shows a power consumption of 232.2 nW at room temperature and maintaining less than 1 ?W even at the peak power consumption of 120℃. This performance is competitive with previously proposed curvature-compensated voltage references [8,11,13]. The performance summary and comparison with recent curvature compensated voltage references are in Table 1.

  This paper presents a sub-BGR with a low TC and low power consumption over a wide temperature range. By employing segmented curvature compensation, the proposed sub-BGR achieves low TC. Moreover, the proposed sub-BGR reuses the bandgap core for both temperature segmentation and segment-wise correction to enhance power and area efficiency. Measurements from 10 chips reveal that the average TC of 17.69 ppm/?C over a temperature range from -40℃ to 120℃. At room temperature, the power consumption is measured at 232.2 nW and the line sensitivity is 0.05 %/V with the supply varying from 1.5 V to 2 V. Based on the measurement results, the prototype sub-BGR shows validate for high-accuracy and power-efficient applications.

  This work was partly supported by the Institute of Information & Communications Technology Planning & Evaluation (IITP)-ITRC (Information Technology Research Center) grant funded by the Korea government (MSIT) (IITP-2025-RS-2023-00260091, 50%) and partly by Korea Institute for Advancement of Technology (KIAT) grant funded by the Korea Government (MOTIE) (P0017011, HRD Program for Industrial Innovation, 50%). The EDA tool was supported by the IC Design Education Center (IDEC), Korea and the chip fabrication was supported by the LX Semicon Co., Ltd.